☰
✕

Constructions
Question
Wired Faculty App

A circle many have ______ parallel tangents.

Answer

two

Sponsor Area

Some More Questions From Constructions Chapter

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that
AB + CD = AD + BC.

In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°. 

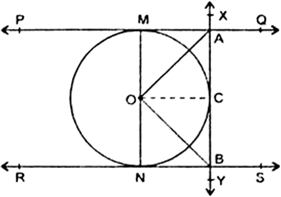
Fig. 10.13

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.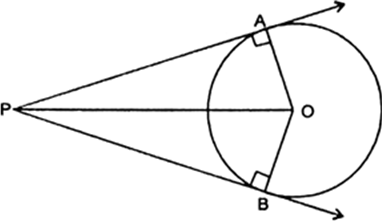

Prove that the parallelogram circumscribing a circle is a rhombus.

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.