Constructions

Question

Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Solution

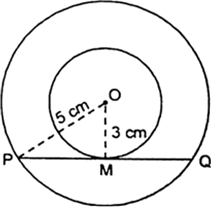
Let O be the common centre of the two concentric circle.
Let PQ be a chord of the larger circle which touches the smaller circle at M.
Join OM and OP.
Since, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore,
∠OMP = 90°
Now,
In ΔOMP, we have
OP² = OM² + PM²[Using Pythagoras theorem]
⇒ (5)² = (3)² + PM²⇒ 25 = 9 + PM²⇒ PM² = 16
⇒ PM = 4 cm
Since, the perpendicular from the centre of a circle to a chord bisects the chord.
Therefore,
PM = MQ = 4 cm
∴ PQ = 2 PM = 2 x 4 = 8 cm
Hence, the required length = 8 cm.

Some More Questions From Constructions Chapter

If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠ POA is equal to
(A) 50° (B) 60°
(C) 70° (D) 80°.

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.