+91-8076753736[email protected]
logo
logo
-->

Constructions

Question
CBSEENMA10008465
Wired Faculty App

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Solution

AB and CD are tangents drawn to the circle at points, P and Q respectively.
Since, a tangent to a circle is perpendicular to the radius through the point of contact.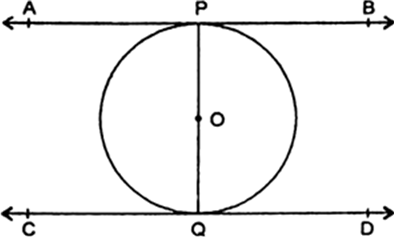

∴ ∠APQ = 90°    ....(i)
and    ∠PQD = 90°    ...(ii)
Comparing (i) and (ii), we get
∠APQ = ∠PQD
But these are the alternate interior angles
∴ AB || CD.

Some More Questions From Constructions Chapter

In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠ POQ = 110°, then ∠ PTQ is equal to
(A) 60°    (B) 70°
(C) 80°    (D) 90°



Fig. 10.11

If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠ POA is equal to

(A) 50°    (B) 60°
(C) 70°    (D) 80°.

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that
AB + CD = AD + BC.

In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°. 

Fig. 10.13

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation