Question
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution
Let ABCD be a parallelogram and a circle with centre O. Let sides AB, BC, CD and AD of the parallelogram touch the circle at E, F, G and H respectively.
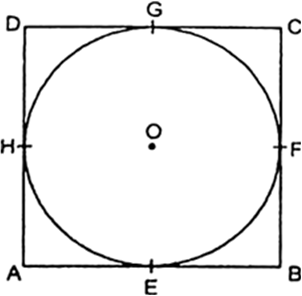
Since, the length of two tangents drawn from an external point to a circle are equal.
So, AE = AH ...(i)
BE = BF ....(ii)
CG = CF ...(iii)
and DG = DH ....(iv)
Adding (i), (ii), (iii) and (iv), we get
AE + BE + GC + DG = AH + BF + CF + DH
⇒ (AE + BE) + (GC + DG)
= (AH + DH) + (BF + CF)
⇒ AB + CD = AD + BC
⇒ 2 AB = 2BC
[∵ ABCD is a || gm So, AB = CD
and BC = AD]
⇒ AB = BC
Similarly, BC = CD and CD = AD
Thus, AB = BC = CD = DA
Hence, ABCD is a rhombus.
