The two circles x2 + y2 = ax and x2 + y2 = c2(c > 0) touch each other if
-
2|a| = c
-
|a| = c
-
a = 2c
-
|a| = 2c
B.
|a| = c
x2 + y2 = ax ...........(1)
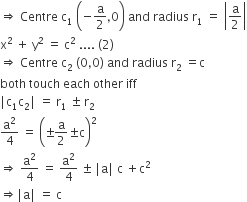
The two circles x2 + y2 = ax and x2 + y2 = c2(c > 0) touch each other if
2|a| = c
|a| = c
a = 2c
|a| = 2c
B.
|a| = c
x2 + y2 = ax ...........(1)
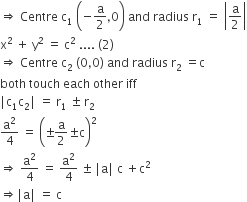
Give an example of a relation which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Determine whether each of the following relations are reflexive, symmetric and transitive :
(i) Relation R in the set A = {1, 2, 3,....., 13, 14} defined as
R = {(x, y) : 3 x – y = 0}
(ii) Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4} (iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x,y) : y is divisible by x} (iv) Relation R in the set Z of all integers defined as R = {(x,y) : x – y is an integer}
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y) : x and y work at the same place}
(b) R = {(x,y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R = {(x, y) : x is wife of y}
(e) R = {(x,y) : x is father of y}
Mock Test Series