+91-8076753736[email protected]
logo
logo
-->

Relations And Functions

Question
CBSEENMA12035637
Wired Faculty App

Find the equation of tangents to the curve y= x3+2x-4, which are perpendicular to line x+14y+3 =0.

Solution

Taking the given equation,
y = x3+2x-4
Differentiating the above function with respect to x, we have,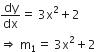
dy over dx equals space 3 straight x squared plus 2 rightwards double arrow space straight m subscript 1 equals space 3 straight x squared plus 2
Given that the tangents to the given curve are perpendicular to the line x+ 14y + 3 = 0
Slope of this line, m2=-1/14
Since the given line and the tangents to the curve are perpendicular, we have,
m1 x m2 =-1
rightwards double arrow space left parenthesis 3 straight x squared plus 2 right parenthesis open parentheses fraction numerator negative 1 over denominator 14 end fraction close parentheses space equals negative 1 rightwards double arrow space 3 straight x squared space plus 2 space equals space 14 rightwards double arrow space 3 straight x squared space equals space 12 rightwards double arrow space straight x squared space equals 4 rightwards double arrow space straight x space equals plus-or-minus 2 If space straight x equals 2 comma space straight y equals straight x cubed space plus 2 straight x minus 4 rightwards double arrow space straight y equals left parenthesis negative 2 right parenthesis cubed plus 2 straight x space left parenthesis negative 2 right parenthesis minus 4 rightwards double arrow straight y equals negative 16 Equation space of space the space tangent space having space slope space straight m space at space the space point space left parenthesis straight x subscript 1 comma straight y subscript 1 right parenthesis space is left parenthesis straight y minus straight y subscript 1 right parenthesis space equals straight m left parenthesis straight x minus straight x subscript 1 right parenthesis Equation space of space the space tangent space at space straight P space left parenthesis 2 comma 8 right parenthesis space with space slope space 14 left parenthesis straight y minus 8 right parenthesis equals 14 left parenthesis straight x minus 2 right parenthesis rightwards double arrow space straight y minus 8 space equals space 14 space straight x minus 28 rightwards double arrow 14 straight x minus straight y equals 20 Equation space of space the space tangent space at space straight P left parenthesis negative 2 comma negative 16 right parenthesis space with space slope space 14 left parenthesis straight y minus 8 right parenthesis equals 14 left parenthesis straight x minus 2 right parenthesis rightwards double arrow space straight y minus 8 space equals space 14 space straight x minus 28 rightwards double arrow 14 space straight x minus straight y space equals 20 Equation space of space the space tangent space at space straight P left parenthesis negative 2 comma negative 16 right parenthesis space with space slope space 1 left parenthesis straight y plus 16 right parenthesis equals 14 left parenthesis straight x plus 2 right parenthesis rightwards double arrow straight y plus 16 space equals space 14 straight x plus 28 rightwards double arrow 14 space straight x minus straight y space equals space minus 12
thus equation of the tangent is 14 x- y =-12

Some More Questions From Relations and Functions Chapter

Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.

Give an example of a relation which is

(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.

Let L be the set of all lines in a plane and R be the relation in L defined as R = {(L1, L2) : L1 is perpendicular to L2}. Show that R is symmetric but neither reflexive nor transitive.

 Determine whether each of the following relations are reflexive, symmetric and transitive :

(i) Relation R in the set A = {1, 2, 3,....., 13, 14} defined as

R = {(x, y) : 3 x – y = 0}

(ii) Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4} (iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x,y) : y is divisible by x} (iv) Relation R in the set Z of all integers defined as R = {(x,y) : x – y is an integer}

(v) Relation R in the set A of human beings in a town at a particular time given by
(a)    R = {(x, y) : x and y work at the same place}
(b)    R = {(x,y) : x and y live in the same locality}
(c)    R = {(x, y) : x is exactly 7 cm taller than y}
(d)    R = {(x, y) : x is wife of y}
(e)    R = {(x,y) : x is father of y}

Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.

Show that the relation R in R defined as R = {(a, b) : a ≤ b}, is reflexive and transitive but not symmetric.

Check whether the relation R in R defined by R = {(a,b) : a ≤ b3} is refleive, symmetric or transitive.

If R and R’ arc reflexive relations on a set then so are R ∪ R’ and R ∩ R’. 

If R and R’ are symmetric relations on a set A, then R ∩ R’ is also a sysmetric relation on A.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation