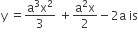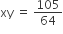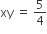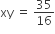Sponsor Area
TextBook Solutions for Nagaland Board Class 11 Mathematics Chapter 11 Conic Section
Question 1
Question 4
Sponsor Area
Sponsor Area
Mock Test Series
Mock Test Series




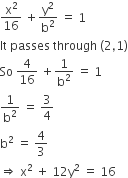



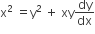
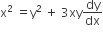
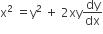
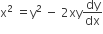
 which of the following remains constant when α varies?
which of the following remains constant when α varies?