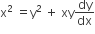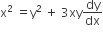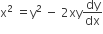Sponsor Area
Conic Section
Question
The differential equation of all circles passing through the origin and having their centres on the x-axis is
Solution
C.
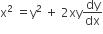
General equation of all such circles is
x2+ y2 + 2gx = 0.
Differentiating, we get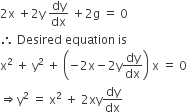
Some More Questions From Conic Section Chapter
The equation of a tangent to the parabola y2 = 8x is y = x + 2. The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is
In an ellipse, the distance between its foci is 6 and minor axis is 8. Then its eccentricity is
If the lines 3x − 4y − 7 = 0 and 2x − 3y − 5 = 0 are two diameters of a circle of area 49π square units, the equation of the circle is
Sponsor Area
Mock Test Series
Mock Test Series