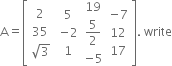Consider the following information regarding the number of men and women workers in three factories I. II and III
|
Men Workers |
Women Workers |
|
|
I |
30 |
25 |
|
II |
25 |
31 |
|
III |
27 |
26 |
Represent the above information in the form of a 3 x 2 matrix. What does the entry in the third row and second column represent?
The given information is
|
Factory |
Men Workers |
Women Worker: |
|
I |
, 30 |
25 |
|
II |
' 25 |
31 |
|
III |
27 |
26 |
The information is represented in the form of a 3 X 2 matrix as follows :![]()
The entry in the third row and second column represents the number of women workers in factory III.