Sponsor Area
Relations And Functions
Consider the following information regarding the number of men and women workers in three factories I. II and III
|
Men Workers |
Women Workers |
|
|
I |
30 |
25 |
|
II |
25 |
31 |
|
III |
27 |
26 |
Represent the above information in the form of a 3 x 2 matrix. What does the entry in the third row and second column represent?
The given information is
|
Factory |
Men Workers |
Women Worker: |
|
I |
, 30 |
25 |
|
II |
' 25 |
31 |
|
III |
27 |
26 |
The information is represented in the form of a 3 X 2 matrix as follows :![]()
The entry in the third row and second column represents the number of women workers in factory III.
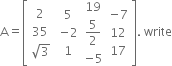
Some More Questions From Relations and Functions Chapter
lf a matrix has 18 elements, what are the possible orders it can have ? What, if it has 5 elements?
If a matrix A has 12 elements, what arc the possible orders it can have 7 What if it has 7 elements ?
Let A be the set of all students of a boys school. Show that the relation R in A given by R = {(a, b) : a is sister of b} is the empty relation and R’ = {(a, b) : the difference between heights of a and b is less than 3 meters} is the universal relation.
Show that the relation R in the set {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} is reflexive but neither symmetric nor transitive.
Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Give an example of a relation which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Let L be the set of all lines in a plane and R be the relation in L defined as R = {(L1, L2) : L1 is perpendicular to L2}. Show that R is symmetric but neither reflexive nor transitive.
Determine whether each of the following relations are reflexive, symmetric and transitive :
(i) Relation R in the set A = {1, 2, 3,....., 13, 14} defined as
R = {(x, y) : 3 x – y = 0}
(ii) Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4} (iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x,y) : y is divisible by x} (iv) Relation R in the set Z of all integers defined as R = {(x,y) : x – y is an integer}
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y) : x and y work at the same place}
(b) R = {(x,y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R = {(x, y) : x is wife of y}
(e) R = {(x,y) : x is father of y}
Determine whether each of the following relations are reflexive, symmetric and transitive :
(i) Relation R in the set A = {1, 2, 3,....., 13, 14} defined as
R = {(x, y) : 3 x – y = 0}
(ii) Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4} (iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x,y) : y is divisible by x} (iv) Relation R in the set Z of all integers defined as R = {(x,y) : x – y is an integer}
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y) : x and y work at the same place}
(b) R = {(x,y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R = {(x, y) : x is wife of y}
(e) R = {(x,y) : x is father of y}
Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.
Sponsor Area
Mock Test Series
Mock Test Series





