Wiredfaculty Logo

For Daily Free Study Material Join wiredfaculty Whatsapp Group | Download Android App | Ncert Book Download

Mathematics Chapter 4 Quadratic Equations

    • Sponsor Area

    NCERT Solution For Class 10 Mathematics

    Quadratic Equations Here is the CBSE Mathematics Chapter 4 for Class 10 students. Summary and detailed explanation of the lesson, including the definitions of difficult words. All of the exercises and questions and answers from the lesson's back end have been completed. NCERT Solutions for Class 10 Mathematics Quadratic Equations Chapter 4 NCERT Solutions for Class 10 Mathematics Quadratic Equations Chapter 4 The following is a summary in Hindi and English for the academic year 2021-2022. You can save these solutions to your computer or use the Class 10 Mathematics.

    Question 1
    CBSEENMA10006442
    Wired Faculty App

    Check whether the following are quadratic equations:
    (x + 1)2 = 2(x – 3)

    Solution

    L.H.S. = (x + 1)2 = x2 + 2x + 1
    R.H.S. = 2(x – 3) = 2x –6
    ∴ 6x2 + 2x + 1 = 2x - 6
    ⇒ x2 + 2x + 1–2x + 6 = 0
    ⇒ x2+ 7 = 0
    ∵ It is of the form ax2 + bx + c = 0, where a = 1,b = 0, c = 7.
    Hence, the given equation is a quadratic equation.

    Question 2
    CBSEENMA10006443
    Wired Faculty App

    Check whether the following are quadratic equations:
    x2 – 2x = (–2) (3 – x)

    Solution

    R.H.S. = (–2) (3 – x) = – 6 + 2x
    ∴ x2 – 2x = – 6 + 2x
    ⇒ x2 – 2x + 6 – 2x = 0
    ⇒ x2 – 4x + 6 = 0
    ∵ It is of the form ax2 + bx + c = 0 where a = 1,b = –4, c = 6.
    Hence, the given equation is a quadratic equation.

    Question 3
    CBSEENMA10006444
    Wired Faculty App

    Check whether the following are quadratic equations:
    (x – 2) (x + 1) = (x – 1) (x + 3)

    Solution

    L.H.S. = (x–2) (x + 1)
    = x2 – x – 2
    R.H.S. = (x – 1) (x + 3)
    = x2 + 2x – 3
    ∴ x2 – x – 2 = x2 + 2x – 3
    ⇒ – x –2 – 2x + 3 = 0
    ⇒ – 3x + 1 = 0
    ∵ It is not of the form ax2 + bx + c = 0.
    Hence, the given equation is not a quadratic equation. 

    Question 4
    CBSEENMA10006445
    Wired Faculty App

    Check whether the following are quadratic equations:
    (x – 3) (2x + 1) = x(x + 5)

    Solution

    L.H.S. = (x – 1) (2x + 1)
    = 2x2 + x – 2x – 1
    = 2x2 – x – 1
    R.H.S. = x(x + 5) = x2 + 5x
    ∴ 2x2 – x – 1 = x2 + 5x
    ⇒ 2x2 – x2 – x – 5x – 1 = 0
    ⇒ x2 – 6x – 1 = 0
    ∵ It is of the form ax2 + bx + c = 0 where a = 1, b = –b, c = –1.
    Hence, the given equation is a quadratic equation.

    Question 5
    CBSEENMA10006447
    Wired Faculty App

    Check whether the following are quadratic equations:
    (2x –1) (x–3) = (x + 5)(x–1)

    Solution

    L.H.S. = (2x – 1) (x – 3)
    = 2x2 – 6x– + 3
    = 2x2 – 7x + 3
    R.H.S. = (x + 5) (a – 1)
    = x2 + 5x – x – 5
    = x2 + 4x – 5
    ∴2x2 – 7x + 3 = x2 + 4x – 5
    ⇒ 2x2 –x2-7x–4x+ 3 + 5 = 0
    ⇒ x2 – 11x + 8 = 0
    ∵ It is of the form ax2 + bx + c = 0 where a = 1, b = –11, c = 8.
    Hence, the given equation is a quadratic equation.

    Question 6
    CBSEENMA10006448
    Wired Faculty App

    Check whether the following are quadratic equations:
    x2 + 3x + 1 = (x – 2)2

    Solution

    R.H.S. = (x – 2)2 = x2 – 4x + 4
    ∴ x2 + 3x + 1 = x2 –4x + 4
    ⇒ 3x + 4x + 1 – 4 = 0
    ⇒ 7x – 3 = 0
    ∵ It is not of the form ax2 + bx + c = 0.
    Hence, the given equation is not a quadratic equation. 

     

    Question 7
    CBSEENMA10006449
    Wired Faculty App

    Check whether the following are quadratic equations:
    (x + 2)3 = 2x(x2 – 1)

    Solution

     L.H.S. = (x + 2)3
    = x3 + 3x2.2 + 3x.(2)2 +8
    = x3 + 6x2 + 12x + 8
    R.H.S. = 2x(x2 – 1) = 2x3– 2x
    ∴ x3 + 6x2 + 12x + 8 = 2x3 - 2x
    ⇒ x3 – 2x3 + 6x2 + 12x + 2x + 8 = 0
    ⇒ –x3 + 6x2 + 14x + 8 = 0
    ∵ It is not of the form ax2 + bx + c = 0.
    Hence, the given equation is not a quadratic equation.

    Question 8
    CBSEENMA10006450
    Wired Faculty App

    Check whether the following are quadratic equations:
    x3 – 4x2 – x + 1 = (x – 2)3.

    Solution

    R.H.S. = (x – 2)3
    = a3 – 23 – 3x.2 (a – 2)
    = x3 – 8 – 6x2 + 12x
    = a3 – 6x2 + 12x – 8
    ∴ x3 – 4x2 – x + 1 = x3 – 6x2 + 12x – 8
    ⇒ –4x2 + 6x2 – x – 12x + 1 + 8 = 0
    ⇒ 2x2– 13x + 9 = 0
    ∵ It is of the form ax2 + bx + c = 0 where a = 2, b = –13, c = 9.
    Hence, the given equation is a quadratic equation.

    Question 9
    CBSEENMA10006451
    Wired Faculty App

    Represent the following problem situations in the form of quadratic equations:
    The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.

    Solution
    Let breadth of the rectangle = x m Then, length of the rectangle = (2x + 1) m
    ∵   Area of the rectangle = (2x + 1) x m2
    According to the given condition,
    (2x + 1)x = 528 ⇒ 2x2 + x – 528 = 0
    which is a quadratic equation in x.
    Solving this equation by factorisation method, we get
                       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow   straight x left parenthesis 2 straight x plus 33 right parenthesis minus 16 left parenthesis 2 straight x plus 33 right parenthesis equals 0
    rightwards double arrow                        <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                2 straight x plus 33 equals 0 space space or space space straight x space minus space 16 space equals space 0
    rightwards double arrow                 space space straight x equals fraction numerator negative 33 over denominator 2 end fraction space space or space space straight x space equals space 16
    But breadth cannot be -ve.
    ∴                                x = 16
    Hence, breadth of the rectangle = 16 m and length of the rectangle = 2 x 16 + 1 = 33 m. 
    Question 10
    CBSEENMA10006453
    Wired Faculty App

    Represent the following problem situations in the form of quadratic equations:
    The product of two consecutive positive integers is 306. We need to find the integers.

    Solution

    Let two consecutive positive integers are x and (x + 1). Then
    x(x + 1) = 306
    ⇒ x2 + x – 306 = 0
    which is a quadratic equation in x.
    Solving this equation by factorisation method, we get
    x2 + 18x – 17x – 306 = 0
    ⇒ x(x + 18) – 17(x + 18) = 0
    ⇒ (x + 18) (x – 17) = 0
    ⇒ x + 18 = 0 or x – 17 = 0
    ⇒ x = –18 or x = 17
    But integers are +ve
    ∴ x = 17
    Hence, two consecutive positive integers are 17 and 18.

    Question 11
    CBSEENMA10006455
    Wired Faculty App

    Represent the following problem situations in the form of quadratic equations:
    Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.

    Solution

    Let Rohan's present age = x years.
    Then, Rohan’s mother age = (x + 26) years
    Rohan’s age after 3 years = (x + 3) years and Rohan’s mother age after 3 yrs.
    = (x + 29) years.
    According to the given condition, (x + 3) (x + 29) = 360
    ⇒ x2 + 32x – 360 =0
    ⇒ x2 + 32x – 273 = 0
    ⇒ x2 + 39x – 7x – 273 = 0
    ⇒ x(x + 39) – 7(x + 39) = 0
    ⇒ (x + 39) (x – 7) = 0
    ⇒ x = –39 or x – 7 = 0 But age cannot be –ve.
    ∴ x = 17
    Hence, Rohan's present age = 7 years.

    Question 12
    CBSEENMA10006458
    Wired Faculty App

    A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
    Solution
    Let the speed of the train = x km/hr Distance = 480 km
    Time taken by the train to cover the distance of 480 km
    equals space 480 over straight x hrs
    Now, according to the given condition,
                  fraction numerator 480 over denominator straight x minus 8 end fraction minus 480 over straight x equals 3
    rightwards double arrow     480 open square brackets fraction numerator 1 over denominator straight x minus 8 end fraction minus 1 over straight x close square brackets equals 3
    rightwards double arrow            open square brackets fraction numerator straight x minus straight x plus 8 over denominator left parenthesis straight x minus 8 right parenthesis. straight x end fraction close square brackets equals 3 over 480
    rightwards double arrow           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow         straight x squared minus 8 straight x minus 1280 equals 0
    rightwards double arrow    straight x squared minus 40 straight x plus 32 straight x minus 1280 equals 0
    rightwards double arrow          <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                 left parenthesis straight x minus 40 right parenthesis left parenthesis straight x plus 32 right parenthesis space equals space 0
    rightwards double arrow     straight x minus 40 space equals space 0 space space space or space space straight x space plus space 32 space equals space 0
    rightwards double arrow                       straight x equals space 40 space space space or space space space straight x space equals space 32.
    But speed of the train cannot be –ve. x = 40. Hence, the speed of the train = 40 km/hr.
    Question 13
    CBSEENMA10006461
    Wired Faculty App

    Find the roots of the following quadratic equations by factorisation method:
    x2 – 3x – 10 = 0

    Solution

    x2 – 3x – 10 = 0
    ⇒ x2 – 5x + 2x– 10 = 0
    ⇒ x(x – 5) + 2(x – 5) =0
    ⇒ (x – 5) (x + 2) = 0
    ⇒ x–5 = 0 or x + 2 = 0
    x = 5 or x = –2
    Hence, the roots of the given quadratic equation are 5 and (-2).

    Question 14
    CBSEENMA10006462
    Wired Faculty App

    Find the roots of the following quadratic equations by factorisation method:
    2x2 + x – 6 = 0

    Solution

    2x2 + x – 6 = 0
    Here, a = 2, b = 1, c = –6
    ac = –12 = 4 x (–3)
    b = 1= 4 – 3
    ∴ 2x2 + x – 6 = 0
    ⇒ 2x2 + 4x – 3x – 6 = 0
    ⇒ 2x(x + 2) – 3(x + 2) = 0
    ⇒ (x + 2) (2x – 3) = 0  
    ⇒  x + 2 = 0 or 2x - 3 = 0
    ⇒   x = –2 or x = 3/2
    Hence, the roots of the given quadratic equation are (-2) and 3/2.

     
    Question 15
    CBSEENMA10006463
    Wired Faculty App

    Find the roots of the following quadratic equations by factorisation method:
    square root of 2 straight x squared plus 7 straight x plus 5 square root of 2 equals 0

    Solution
    square root of 2 straight x squared plus 7 straight x plus 5 square root of 2 equals 0
    rightwards double arrow      square root of 2 straight x squared plus 5 straight x plus 2 straight x plus 5 square root of 2 equals 0
    rightwards double arrow   space space space space space space space space space space space space space straight x left parenthesis square root of 2 straight x plus 5 right parenthesis space plus space square root of 2 left parenthesis square root of 2 straight x plus 5 right parenthesis space equals 0
    rightwards double arrow                 left parenthesis square root of 2 straight x plus 5 right parenthesis space left parenthesis straight x plus square root of 2 right parenthesis space space equals 0
    rightwards double arrow                       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Hence, the roots of the given quadratic equation are space space fraction numerator negative 5 over denominator square root of 2 end fraction space and space minus square root of 2.
    Question 16
    CBSEENMA10006465
    Wired Faculty App

    Find the roots of the following quadratic equations by factorisation method:
    2 straight x squared minus straight x plus 1 over 8 equals 0

    Solution
    2 straight x squared minus straight x plus 1 over 8 equals 0  
         rightwards double arrow     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
         rightwards double arrow     16 straight x squared minus 4 straight x minus 4 straight x plus 1 equals 0
    rightwards double arrow 4 straight x left parenthesis 4 straight x minus 1 right parenthesis minus 1 left parenthesis 4 straight x minus 1 right parenthesis space equals space 0
    rightwards double arrow             left parenthesis 4 straight x minus 1 right parenthesis space left parenthesis 4 straight x minus 1 right parenthesis space equals space 0
    rightwards double arrow                <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                   4 straight x minus 1 space equals space 0
    rightwards double arrow                         <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    So, this root is repeated twice.
    Hence, both the roots of the given quadratic equation are 1 fourth.
    Question 17
    CBSEENMA10006468
    Wired Faculty App

    Find the roots of the following quadratic equations by factorisation method:
          <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow          100 straight x squared minus 10 straight x minus 10 straight x plus 1 equals 0
    rightwards double arrow   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow               left parenthesis 10 straight x minus 1 right parenthesis space left parenthesis 10 straight x minus 1 right parenthesis space equals space 0
    rightwards double arrow                   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                     space 10 straight x minus 1 equals 0
    rightwards double arrow                                   space space space straight x equals 1 over 10
    So, this root is repeated twice.
    Hence, both the roots of the given quadratic equation are <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>.

    Sponsor Area

    Question 18
    CBSEENMA10006469
    Wired Faculty App

    John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.

    Solution
    Let the number of marbles John had = x Then, the number of marbles Jivanti had = (45 – x).
    According to the given question,
    (x – 5) (45 – x – 5) = 124
    ⇒ (x – 5) (40 – x) – 124 = 0
    ⇒ 40x – x2 – 200 + 5x– 124 =0
    ⇒ –x2 + 45x – 324 =0
    ⇒ x2 – 45x + 324 = 0
    x2 – 36x – 9x + 324 = 0
    ⇒ x(x – 36) – 9(x – 36) = 0
    ⇒ (x – 36) (x – 9) = 0
    x – 36 = 0 or x – 9 = 0
    x = 36 or x = 9
    Hence, the number of marbles John had = 36 and the number of marbles Jivanti had = 45 - 36 = 9.
    Question 19
    CBSEENMA10006471
    Wired Faculty App

    A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of articles produced in a day. On a particular day, the total cost of production was Rs. 750. We would like to find out the number of toys produced on that day.

    Solution

    Let the number of toys produced on that day = x
    And, cost of production = (55 – x)
    According to the given question,
    x (55 – x) = 750
    ⇒ 55x – x2 – 750 = 0
    x2 – 55x + 750 = 0
    ⇒ x2 – 30x – 25x + 750 = 0
    ⇒ x(x – 30) – 25(x – 30) = 0
    ⇒ (x – 30) (x – 25) = 0
    ⇒ x – 30 = 0 or x – 25 = 0
    ⇒ x = 30 or x = 25.
    Hence, the number of toys produced on that day are 30 or 25.

    Question 20
    CBSEENMA10006472
    Wired Faculty App

    Find two numbers whose sum is 27, and product is 182.

    Solution
    Let the first number be x so, second number = 27 - x.
    According to question,
    x(27 – x) = 182
    ⇒ 27x – x2 = 182
    ⇒ x2 – 27x + 182 = 0
    ⇒ x2 – 14x – 13x + 182 = 0
    ⇒ x(x – 14) – 13 (x– 14) = 0
    ⇒ (x – 13) (x – 14) = 0
    Either x – 13 = 0 or x – 14 = 0
    ⇒ x = 13 or x = 14
    If x = 13 then other number = 21 – x
    = 27 – 13 = 14 If x = 14 then other number = 27 - x
    = 27 – 14 = 13 Hence, required two numbers are 13 and 14.
    Question 21
    CBSEENMA10006475
    Wired Faculty App

    Find two consecutive positive integers, sum of whose square is 365.

    Solution
    Let first positive integer be x
    So, other positive integer = x + 1
    According to question,
    x2 + (x + 1)2 = 365 x2 + x2 + 1 + 2x = 365
    ⇒ 2x2 + 2x – 364 = 0
    ⇒ x2 + x – 182 = 0
    ⇒ x2 + 14x – 13x – 182 = 0
    ⇒ x(x + 14) – 13(x + 14) = 0
    ⇒ (x – 13) (x + 14) = 0
    ⇒ x – 13 = 0
    or x + 14 = 0
    ⇒ x = 13
    or x = –14
    Here x = – 14 does not exist.
    Therefore, required positive integers are : x = 13 and x + 1 = 13 + 1 = 14.
    Question 22
    CBSEENMA10006485
    Wired Faculty App

    The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm. Find the other two sides.

    Solution

    Let the base (BC) of the right triangle = x cm
    So, altitude (AB) = (x – 7) cm
    And hypotenuse (AC) = 13 cm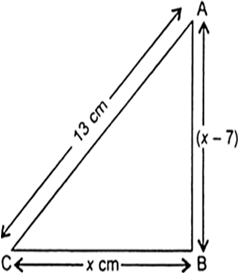

    According to Pythagoras theorem,
    AC2 = AB2 + BC2 ⇒ (13)2 = (x – 7)2 + (x)2
    ⇒ 169 = x2 + 49 – 14x + x2
    ⇒ 169 = 2x2 – 14x + 49
    ⇒ 2x2 – 14x – 120 = 0
    ⇒ x2 – 7x – 60 = 0
    ⇒ x2 – 12x + 5x – 60 = 0
    ⇒ x(x - 12) + 5(x – 12) = 0
    ⇒ (x + 5) (x – 12) = 0
    ⇒ x + 5 = 0
    or x- 12 = 0
    ⇒ x = –5
    or x = 12
    Since side of triangle is never negative So,
     x = 12
    Now required sides of the triangle are
    AB = x – 7
    = 12 – 7 = 5 cm
    BC = x = 12 cm.

    Question 23
    CBSEENMA10006493
    Wired Faculty App

    A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs. 90. Find the number of articles produced and the cost of each article.

    Solution

    Let the number of articles produced be x
    Therefore, cost of production of each article (in Rs.) on that particular day = Rs. (2x + 3)
    So, total cost of production that day = Rs. x(2x + 3)
    According to question,
                           x(2x+3) = 90
    rightwards double arrow               2 straight x squared plus 3 straight x equals 90
    rightwards double arrow             space 2 straight x squared plus 3 straight x minus 90 equals 0
    rightwards double arrow           space space space space space space space 2 straight x squared plus 15 straight x minus 12 straight x minus 90 space equals space 0
    rightwards double arrow        straight x left parenthesis 2 straight x plus 15 right parenthesis minus 6 left parenthesis 2 straight x plus 15 right parenthesis space equals 0
    rightwards double arrow                  left parenthesis straight x minus 6 right parenthesis space left parenthesis 2 straight x plus 15 right parenthesis space equals space 0
    rightwards double arrow                            straight x minus 6 space equals space 0
    or                   space space 2 straight x plus 15 space equals space 0
             rightwards double arrow                 <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    or                       2 straight x space equals space minus 15
             rightwards double arrow            straight x equals fraction numerator negative 15 over denominator 2 end fraction
    Since straight x equals fraction numerator negative 15 over denominator 2 end fraction is not possible
    So, x = 6
    Hence, number of articles produced be x = 6 And cost of production of each article = Rs. (2x + 3)= Rs. (2 x 6 + 3) = Rs. (15).

    Question 24
    CBSEENMA10006495
    Wired Faculty App

    Find the roots of the following quadratic equations, if they exist by the method of completing the square:
    2x2 –7x + 3 = 0

    Solution
    2x2 – 7x + 3 = 0
    rightwards double arrow     space space space space space straight x squared minus 7 over 2 straight x plus 3 over 2 equals 0 space space space space space space space left square bracket Dividing space by space 2 right square bracket
    rightwards double arrow space space space open curly brackets straight x squared minus 2. straight x.7 over 4 plus open parentheses 7 over 4 close parentheses squared close curly brackets minus open parentheses 7 over 4 close parentheses squared plus 3 over 2 equals 0
    rightwards double arrow         <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                  open parentheses straight x minus 7 over 4 close parentheses squared space equals space 25 over 16
    rightwards double arrow              space space space space straight x minus 7 over 4 equals plus-or-minus 5 over 4
    rightwards double arrow               straight x equals 7 over 4 plus-or-minus 5 over 4 equals fraction numerator 7 plus 5 over denominator 4 end fraction comma space fraction numerator 7 minus 5 over denominator 4 end fraction
    rightwards double arrow             straight x equals 12 over 4 comma space 2 over 4 equals 3 comma space 1 half.
    Hence, the roots of the given quadratic equations are  3 and 1 half.
    Question 25
    CBSEENMA10006496
    Wired Faculty App

    Find the roots of the following quadratic equations, if they exist by the method of completing the square:
    2 straight x squared plus straight x minus 4 space equals space 0

    Solution
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow       straight x squared plus 1 half straight x minus 2 equals 0 space space left square bracket Dividing space by space 2 right square bracket
    rightwards double arrow       space space space space space space space space space open curly brackets straight x squared plus 2. straight x.1 fourth plus open parentheses 1 fourth close parentheses squared close curly brackets minus open parentheses 1 fourth close parentheses squared minus 2 equals 0
    rightwards double arrow      <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
     
    rightwards double arrow           space space space space space open parentheses straight x plus 1 fourth close parentheses squared space minus space 33 over 16 space equals space 0
    rightwards double arrow            space space open parentheses straight x plus 1 fourth close parentheses squared space equals space 33 over 16
    rightwards double arrow             space space straight x plus 1 fourth equals plus-or-minus fraction numerator square root of 33 over denominator 4 end fraction
     
    rightwards double arrow               straight x equals negative 1 fourth plus-or-minus fraction numerator square root of 33 over denominator 4 end fraction
    rightwards double arrow             straight x equals fraction numerator negative 1 plus-or-minus square root of 33 over denominator 4 end fraction

    Hence, the roots of the given quadratic equations are : fraction numerator negative 1 plus-or-minus square root of 33 over denominator 4 end fraction space and space fraction numerator negative 1 minus square root of 33 over denominator 4 end fraction.
    Question 26
    CBSEENMA10006497
    Wired Faculty App

    Find the roots of the following quadratic equations, if they exist by the method of completing the square:
    4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0

    Solution
    4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0 rightwards double arrow space space space open curly brackets left parenthesis 2 straight x right parenthesis squared plus 2. left parenthesis 2 straight x right parenthesis. square root of 3 plus left parenthesis square root of 3 right parenthesis squared close curly brackets space equals space 0 rightwards double arrow space space space space space space space space left parenthesis 2 straight x plus square root of 3 right parenthesis squared space equals space 0
    rightwards double arrow              2 straight x plus square root of 3 space equals space 0
    rightwards double arrow                       straight x equals negative fraction numerator square root of 3 over denominator 2 end fraction.
    So, this root is repeated twice.
    Hence, both the roots of the given equations are open parentheses negative fraction numerator square root of 3 over denominator 2 end fraction close parentheses.
    Question 27
    CBSEENMA10006498
    Wired Faculty App

    Find the roots of the following quadratic equations, if they exist by the method of completing the square:
    2x2+x+ 4 = 0.

    Solution
    space space 2 straight x squared plus straight x plus 4 space equals space 0 space space rightwards double arrow space space space space space straight x squared plus 1 half straight x plus 2 space equals space 0 space space space space space left square bracket Dividing space by space 2 right square bracket
    rightwards double arrow          space space space open curly brackets straight x squared plus 2. straight x.1 fourth plus open parentheses 1 fourth close parentheses squared close curly brackets minus open parentheses 1 fourth close parentheses squared plus 2 equals 0  
                                                          [Completing the square]
    rightwards double arrow              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    rightwards double arrow         open parentheses straight x plus 1 fourth close parentheses squared plus 31 over 16 equals 0
    rightwards double arrow                   open parentheses straight x plus 1 fourth close parentheses squared space equals space minus 31 over 16
     
    rightwards double arrow                  space space space space space space straight x plus 1 fourth equals plus-or-minus fraction numerator square root of negative 31 end root over denominator 4 end fraction
     
    rightwards double arrow                 straight x equals negative 1 fourth plus-or-minus fraction numerator square root of negative 31 end root over denominator 4 end fraction
    rightwards double arrow              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Hence, the given quadratic equation have no real roots. 
    Question 28
    CBSEENMA10006499
    Wired Faculty App

    Find the roots of the quadratic equations given in Q. 1, above by applying the quadratic formula.

    Solution

    (i) We have,
    2x2 – 1x + 3 = 0
    Here, a = 2, b = –7 and c = 3
    Now, b2 – = (–7)2 – 4(2) (3)
    = 49 – 24 = 25 Since, b2 – 4ac > 0
    Therefore, the quadratic equation 2x2 – 1x + 3 = 0 has distinct roots i.e. α and β.
    Now,    <pre>uncaught exception: <b>file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php at line #12file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php line 12<br />#0 [internal function]: _hx_error_handler(2, 'file_put_conten...', '/home/config_ad...', 12, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php(12): file_put_contents('/home/config_ad...', 'mml=<math xmlns...') #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(48): sys_io_File::saveContent('/home/config_ad...', 'mml=<math xmlns...') #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(112): com_wiris_util_sys_Store->write('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #6 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #7 {main}</pre>
    equals fraction numerator negative left parenthesis negative 7 right parenthesis plus-or-minus square root of 25 over denominator 2 cross times 2 end fraction equals fraction numerator 7 plus-or-minus 5 over denominator 4 end fraction
    So,             straight alpha space equals space fraction numerator 7 plus 5 over denominator 4 end fraction equals 12 over 4 equals 3 straight beta space equals space fraction numerator 7 minus 5 over denominator 4 end fraction equals 2 over 4 equals 1 half
    Therefore, the required roots are 3 and 1 half.

    (ii) We have,
    2x2 + x – 4 = 0
    Here, a = 2, b = 1 and c = –4
    Now, b2 – 4ac = (1)2 –4 (2) (–4)
    = 1 + 32 = 33
    Since, b2 – 4ac > 0
    Therefore, the quadratic equation 2x2 + x – 4 = 0 has distinct roots i.e. α and 946;.
    Now,       <pre>uncaught exception: <b>file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php at line #12file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/df/c4/16fdd78514dd5dbd680547adbe01.ini): failed to open stream: Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php line 12<br />#0 [internal function]: _hx_error_handler(2, 'file_put_conten...', '/home/config_ad...', 12, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php(12): file_put_contents('/home/config_ad...', 'mml=<math xmlns...') #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(48): sys_io_File::saveContent('/home/config_ad...', 'mml=<math xmlns...') #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(112): com_wiris_util_sys_Store->write('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #6 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #7 {main}</pre>
                      equals fraction numerator negative 1 plus-or-minus square root of 33 over denominator 2 left parenthesis 2 right parenthesis end fraction equals fraction numerator negative 1 plus-or-minus square root of 33 over denominator 4 end fraction
    So,           straight alpha equals fraction numerator negative 1 plus square root of 33 over denominator 4 end fraction
                    straight beta equals fraction numerator negative 1 minus square root of 33 over denominator 4 end fraction

    (iii) We have,
             4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0
    Here, <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Now,     straight b squared minus 4 ac space equals space left parenthesis 4 square root of 3 right parenthesis squared minus 4 space left parenthesis 4 right parenthesis space left parenthesis 3 right parenthesis
                                  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Since,  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Therefore, the quadratic equation 4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0  has equal roots i.e. straight alpha equals straight beta
    Now,         space straight x equals fraction numerator negative straight b plus-or-minus square root of straight b squared minus 4 ac end root over denominator 2 straight a end fraction space space space space equals space fraction numerator negative 4 square root of 3 plus-or-minus 0 over denominator 2 cross times 4 end fraction equals fraction numerator negative 4 square root of 3 over denominator 8 end fraction
         Therefore, the requried roots are equals fraction numerator negative square root of 3 over denominator 2 end fraction. 

    (iv) We have,
    2x2 + x + 4 = 0
    Here, a = 2, b = 1 and c = 4
    Now, b2 – 4ac = (1)2 – 4(2) (4)
    = 1 – 32 = – 31
    Since, b2 – 4ac = 0
    Therefore, the quadratic equation 2x2 + x + 4 = 0 has no roots.

    Question 29
    CBSEENMA10006501
    Wired Faculty App

    Find the roots of the factors of equations:
        straight x minus 1 over straight x equals 3 comma space space straight x not equal to 0.

    Solution

    We have,
             straight x minus 1 over straight x equals 3
    rightwards double arrow          fraction numerator straight x squared minus 1 over denominator straight x end fraction equals 3
    rightwards double arrow       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow       straight x squared minus 3 straight x minus 1 space equals space 0
    Here,   straight a equals 1 comma space space straight b equals negative 3 space and space straight c space equals space minus 1
    Now,             straight b squared minus 4 ac equals left parenthesis negative 3 right parenthesis squared minus 4 left parenthesis 1 right parenthesis left parenthesis negative 1 right parenthesis space space space space space space space space space space space space space space space equals 9 plus 4 equals 13 Since comma space space straight b squared minus 4 ac greater than 0
    Therefore, quadratic equation x2 – 3x – 1 =0 has distinct roots, i.e. α and β.
    Now,   straight x equals fraction numerator negative straight b plus-or-minus square root of straight b squared minus 4 ac end root over denominator 2 straight a end fraction space space equals space fraction numerator negative left parenthesis negative 3 right parenthesis plus-or-minus square root of 13 over denominator 2 left parenthesis 1 right parenthesis end fraction equals fraction numerator 3 plus-or-minus square root of 13 over denominator 2 end fraction
    So,     space space space straight alpha space equals space fraction numerator 3 plus square root of 13 over denominator 2 end fraction
    and       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
       Therefore, the required roots are 
                    fraction numerator 3 plus square root of 13 over denominator 2 end fraction space and space fraction numerator 3 minus square root of 13 over denominator 2 end fraction.

    Question 30
    CBSEENMA10006503
    Wired Faculty App

    The sum of the reciprocals of Rehman’s age (in years) 3 years ago and 5 years from now is space 1 third.
    Find his present age.

    Solution
    Let the present age of Rehman = x years
    3 years ago, his age was = (x – 3) years and 5 years from now his age will be = (x + 5) years
    Now. according to the given problem, we have
    fraction numerator 1 over denominator straight x minus 3 end fraction plus fraction numerator 1 over denominator straight x plus 5 end fraction equals 1 third
    rightwards double arrow    fraction numerator straight x plus 5 plus straight x minus 3 over denominator left parenthesis straight x minus 3 right parenthesis left parenthesis straight x plus 5 right parenthesis end fraction equals 1 third
    rightwards double arrow       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>    
    rightwards double arrow          straight x squared plus 2 straight x minus 15 space equals space 3 left parenthesis 2 straight x plus 2 right parenthesis
    rightwards double arrow           space straight x squared plus 2 straight x minus 15 space equals space 6 straight x plus 6
    rightwards double arrow  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow          <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow    straight x squared minus 7 straight x plus 3 straight x minus 21 space equals 0
    rightwards double arrow    straight x open parentheses straight x minus 7 close parentheses plus 3 left parenthesis straight x minus 7 right parenthesis space equals space 0
    rightwards double arrow           left parenthesis straight x minus 7 right parenthesis space left parenthesis straight x plus 3 right parenthesis space equals space 0
    rightwards double arrow                   straight x minus 7 equals 0 space or space straight x plus 3 equals 0
    rightwards double arrow                        space space straight x equals 7 space or space straight x space equals space minus 3
    But age cannot be –ve. ∴ x = 7.
    Hence, the present age of Rehman = 7 years. 
    Question 31
    CBSEENMA10006504
    Wired Faculty App

    In a class, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product would have been 210. Find her marks in the two subjects.

    Solution

    Let marks got by Shefali in Mathematics = x
    Then, marks got by her in English = (30 – x)
    Now, according to the given problem, we have
    (x + 2) (30 – x – 3) = 210 (x + 2) (27 – x) = 210
    ⇒ 27x – x2 + 54 – 2x – 210 = 0
    ⇒ –x2 + 25x – 156 = 0
    ⇒ x2 – 25x + 156 = 0
    x2 – 13x – 12x + 156 = 0
    ⇒ x(x – 13) – 12(x – 13) = 0
    ⇒ (x – 13) (x – 12) = 0
    ⇒ x – 13 = 0 or x –12 = 0
    x = 13 or x = 12
    Hence, if marks got by Shefali in Mathematics = 13 then marks got by her in English 30 – 13 = 17 Ans.
    and if marks got by Shefali in Mathematics = 12 then marks got by her in English = 30 – 12 = 18 Ans. 

    Question 32
    CBSEENMA10006506
    Wired Faculty App

    The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.

    Solution
    Let the shorter side of the field = x m
    Then, longer side of the field = (x + 30) m and diagonal of the field = (x + 60) m

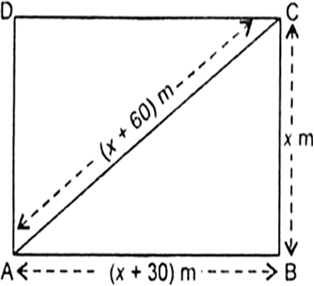
    Now, in right ΔABC, by Pythagoras theorem, we have
    AB2 + BC2 = AC2
    ⇒ (x + 30)2 + x2 = (x + 60)2
    ⇒ x2 + 60x + 900 + x2 = x2 + 120x + 3600
    ⇒ 2x2 + 60x + 900 = x2 + 120x + 3600
    ⇒ 2x2 – x2 + 60x – 120x + 900 – 3600 = 0
    ⇒ x2 – 60x – 2700 = 0
    which is a quadratic equation in x.
    We can solve it by quadratic formula
    Here,    a = 1,   b = -60,   c=-2700
    ∴          straight D equals straight b squared minus 4 ac
                    equals left parenthesis negative 60 right parenthesis squared minus 4 cross times 1 cross times left parenthesis negative 2700 right parenthesis
                     space space equals 3600 plus 10800 equals 14400
    ∴    space space space space space space straight x equals fraction numerator negative straight b plus-or-minus square root of straight D over denominator 2 straight a end fraction equals fraction numerator 60 plus-or-minus square root of 14400 over denominator 2 end fraction
                   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    But side of a rectangle cannot be –ve.
    ∴ x = 90
    Hence, the shorter side of the field = 90 m and the longer side of the field = 90 + 30 = 120 m. Ans.
    Question 33
    CBSEENMA10006507
    Wired Faculty App

    The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.

    Solution

    Let the smaller number = x
    and            the larger number = y
            Then,          straight x squared space equals space 8 straight y              ...(i)
    and               straight y squared minus straight x squared space equals space 180          ...(ii)
        From (i) and (ii), we get
                            <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow     straight y squared minus 8 straight y minus 180 space equals space 0
    which is a quadratic equation in y. We can solve it by factorisation method.
                           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow          straight y squared minus 8 straight y minus 180 space equals space 0
    which is a quadratic equation in y. We can solve it by factorisation method.
    rightwards double arrow space space space straight y squared minus 18 straight y plus 10 straight y minus 180 equals 0 rightwards double arrow space space straight y left parenthesis straight y minus 18 right parenthesis space plus space 10 left parenthesis straight y minus 18 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space left parenthesis straight y minus 18 right parenthesis space left parenthesis straight y plus 10 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space straight y minus 18 space equals space 0 space space space space space or space space straight y space plus space 10 space equals 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space straight y space equals space 18 space space space or space space straight y space equals space minus 10
    When y = -10,  then straight x squared equals negative 80
    rightwards double arrow                           straight x equals plus-or-minus square root of negative 80 end root space not an element of space straight R
    ∴                              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    When y = 18, then  straight x equals 8 cross times 18 space equals space 144
     rightwards double arrow                               <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    If smaller number  = 12
    Then, larger number = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    If smaller number  = -12
    Then, larger number = fraction numerator left parenthesis negative 12 right parenthesis squared over denominator 8 end fraction equals 144 over 8 equals 18 space Ans. space
    Hence, the required numbers are 18, 12 or 18, –12. Ans.

    Question 34
    CBSEENMA10006509
    Wired Faculty App

    A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, would have taken 1 hour less for the same journey. Find the speed of the train.

    Solution
    Let the speed of the train = x km/hr
    Distance = 360 km
    ∴   Time taken to cover 360 km = space 360 over straight x hr.
    If the speed had been 5 km/hr more, then
    time taken to cover 360 km = 360/x + 5
    Now, according to the given problem,
                 <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                   fraction numerator 360 cross times 5 over denominator straight x squared plus 5 straight x end fraction equals 1
    rightwards double arrow                        space space straight x squared plus 5 straight x equals 1800
    rightwards double arrow          <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    which is a quadratic equation in x. It can be solved by factorisation method.
    ⇒ x2 + 45x – 40x – 1800 = 0
    ⇒ x (x + 45) – 40 (x + 45) = 0
    ⇒ (x + 45) (x – 40) = 0
    ⇒ x + 45 = 0 or x – 40 =0
    ⇒ x = – 45 or x = 40
    But speed of the train cannot be –ve.
    ∴ x = 40
    Hence, speed of the train = 40 km/hr. Ans.
    Question 35
    CBSEENMA10006511
    Wired Faculty App

    Two water taps together can fill a tank in space 9 3 over 8 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.

    Solution
    Suppose the time taken by the larger tap to fill the tank is x hours.
    ∴     Time taken by the smaller tap to fill the tank = (x + 10) hours
     Now, Portion of the tank filled by the larger tank  in 1 hour = 1 over straight x
    Portion of the tank filled by the smaller tank in 1 hour = fraction numerator 1 over denominator straight x plus 10 end fraction and Portion of the tank filled by the both in 1 hour
    equals 1 over straight x plus fraction numerator 1 over denominator straight x plus 10 end fraction equals fraction numerator straight x plus 10 plus straight x over denominator straight x left parenthesis straight x plus 10 right parenthesis end fraction equals space fraction numerator 2 straight x plus 10 over denominator straight x left parenthesis straight x plus 10 right parenthesis end fraction equals fraction numerator 2 left parenthesis straight x plus 5 right parenthesis over denominator straight x left parenthesis straight x plus 10 right parenthesis end fraction space space space... left parenthesis straight i right parenthesis
    It is given that,
    Portion of the tank filled by both in 1 hour  = 8 over 75
                                                                         ..(ii)
    ∴   From (i) and (ii), we get
                            <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow space space space space space space space space space space space space space space space space space space space fraction numerator straight x plus 5 over denominator straight x squared plus 10 straight x end fraction equals 4 over 75 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space 75 straight x plus 375 space equals space 4 straight x squared plus 40 straight x rightwards double arrow space space space space space 4 straight x squared plus 40 straight x minus 75 straight x minus 375 space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space 4 straight x squared minus 35 straight x minus 375 space equals space 0 space therefore space space space space space space space space space space space straight x space equals space fraction numerator 35 plus-or-minus square root of left parenthesis 35 right parenthesis squared minus 4 cross times 4 cross times left parenthesis negative 375 right parenthesis end root over denominator 2 cross times 4 end fraction space space space space space space space space space space space space space space space space space space space space space equals space fraction numerator 35 plus-or-minus square root of 1225 plus 6000 end root over denominator 8 end fraction space space space space space space space space space space space space space space space space space space space space space space equals space fraction numerator 35 plus-or-minus square root of 7225 over denominator 8 end fraction equals fraction numerator 35 plus-or-minus 85 over denominator 8 end fraction
                         
                      equals fraction numerator 35 plus 85 over denominator 8 end fraction space or space fraction numerator 35 minus 85 over denominator 8 end fraction
                       equals space 120 over 8 space or space fraction numerator negative 50 over denominator 8 end fraction
                        <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>              space space open square brackets fraction numerator negative 50 over denominator 8 end fraction space is space rejected close square brackets
    Hence, Time taken by the larger tap = 15 hrs and time taken by the smaller tap = (15 +10) = 25 hrs.
    Question 36
    CBSEENMA10006512
    Wired Faculty App

    An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speed of the two trains.

    Solution
    Let the average speed of the passenger train = x km/hr
    Then, the average speed of the express train = (x + 11) km/hr
    Distance = 132 km
    Time taken by the passenger train to cover 132 km = 132 over straight x space hrs.
    and the time taken by express train to cover 132 km = fraction numerator 132 over denominator straight x plus 11 end fraction hrs.
    Now, according to the given problem,
               space space space space space 132 over straight x minus fraction numerator 132 over denominator straight x plus 11 end fraction equals 1
     rightwards double arrow    132 open square brackets 1 over straight x minus fraction numerator 1 over denominator straight x plus 11 end fraction close square brackets space equals space 1
    rightwards double arrow            fraction numerator straight x plus 11 minus straight x over denominator straight x left parenthesis straight x plus 11 right parenthesis end fraction space equals space 1 over 132
    rightwards double arrow            space space fraction numerator 11 over denominator straight x squared plus 11 straight x end fraction equals 1 over 132
    rightwards double arrow         space space space straight x squared plus 11 straight x equals space 132 cross times 11
    rightwards double arrow     space space straight x squared plus 11 straight x minus 1452 equals 0
    which is a quadratic equation in x.
    We can solve this equation by quadratic formula.
    Here,  a = 1,  b = 11, c = -1452
    ∴        <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Now,    straight x equals fraction numerator negative straight b plus-or-minus square root of straight D over denominator 2 straight a end fraction equals fraction numerator negative 11 plus-or-minus square root of 5929 over denominator 2 cross times 1 end fraction
                   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    But speed of the train cannot be -ve.
    ∴ x = 33
    Hence, the average speed of the passenger train
    = 33 + 11 = 44 km/hr.
    Question 37
    CBSEENMA10006513
    Wired Faculty App

    Sum of the area of the two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.

    Solution

    Let the side of first square = x m and the side of second square = y m
    Then, the area of first square = x2 m2 and the area of second square = y2 m2 Perimeter of the first square = 4x m and perimeter of the second square = 4y m
    Now, according to the given problem, we have x2 + y2 = 468 ...(i)
    and 4x – 4y = 24
    ⇒ x – y = 6 ...(ii)
    From equation (ii), we get
    x – 6 + y = 0 ...(iii)
    Putting this value of x in (i), we get
    (6 + y)2 + y2 = 468 ⇒ 36+12y + f + y2 = 468 ⇒ 2y2 + 12y + 36 – 468 =0
    ⇒ 2y2 + 12y – 432 = 0
    ⇒ y2 + 6y – 216 = 0 which is a quadratic equation in y.
    We can solve this equation by quadratic formula.
    Here,  a = 1,  b = 6,  c = -216
    ∴         straight D equals straight b squared minus 4 ac space space space equals space left parenthesis 6 right parenthesis squared minus 4 cross times 1 cross times left parenthesis negative 216 right parenthesis space space space space equals 36 plus 864 space equals space 900
    Now,    straight y equals fraction numerator negative straight b plus-or-minus square root of straight D over denominator 2 straight a end fraction equals fraction numerator negative 6 plus-or-minus square root of 900 over denominator 2 cross times 1 end fraction space space space equals space fraction numerator negative 6 plus-or-minus 30 over denominator 2 end fraction space equals space 24 over 2 comma space space fraction numerator negative 36 over denominator 2 end fraction space equals space 12 comma space space minus 18
    But the side of a square cannot be -ve. y = 12 Putting this value of y in (iii), we get
    x = 6 + 12 = 18 Hence, the side of the first square = 18 m and the side of the second square = 12 m. Ans.

    Question 38
    CBSEENMA10006514
    Wired Faculty App

    Find the discriminant of the following quadratic equations. If the real roots exist, find them
    2 straight x squared minus 3 straight x plus 5 space equals space 0

    Solution

    We have,
               2 straight x squared minus 3 straight x plus 5 equals 0
    Here,    straight a equals 2 comma space space space space space straight b space equals space minus 3 comma space space space straight c space equals space 5
    Now,                   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Since,     D < 0
    Therefore, the given quadratic equation has no real roots.

    Question 39
    CBSEENMA10006517
    Wired Faculty App

    Find the discriminant of the following quadratic equations. If the real roots exist, find them
    3 straight x squared minus 4 square root of 3 straight x plus 4 equals 0

    Solution

    We have,
      <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Here,   straight a equals 3 comma space space space straight b equals negative 4 square root of 3 comma space space straight c space equals space 4
    Now,              straight D equals straight b squared minus 4 ac space space space space equals space open parentheses negative 4 square root of 3 close parentheses squared minus 4 left parenthesis 3 right parenthesis left parenthesis 4 right parenthesis space space space space equals space 48 minus 48 space equals space 0
    Since,              D = 0
    Therefore, the given quadratic equation has equal roots.
    Now,  straight x equals fraction numerator negative straight b plus-or-minus square root of straight D over denominator 2 straight a end fraction equals fraction numerator negative left parenthesis negative square root of 3 right parenthesis plus-or-minus square root of 0 over denominator 2 left parenthesis 3 right parenthesis end fraction
                <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Hence, roots are fraction numerator 2 square root of 3 over denominator 3 end fraction comma space fraction numerator 2 over denominator square root of 3 end fraction.

    Sponsor Area

    Question 40
    CBSEENMA10006518
    Wired Faculty App

    Find the discriminant(or the nature of the roots) of the following quadratic equations. If the real roots exist, find them
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    2x2 – 6x + 3 = 0
    Here, a = 2, b = –6, c = 3
    Now, D = b2 – 4ac
    = (–6)2 – 4(2) (3)
    = 36 – 24 = 12
    Since, D > 0
    Therefore, the given quadratic equation has real and distinct roots.
    Now,    straight x space equals space fraction numerator negative straight b plus-or-minus square root of straight D over denominator 2 straight a end fraction equals fraction numerator left parenthesis negative 6 right parenthesis plus-or-minus square root of 2 over denominator 2 cross times 2 end fraction space space space equals space fraction numerator 6 plus-or-minus 2 square root of 3 over denominator 4 end fraction space equals space fraction numerator 3 plus-or-minus square root of 3 over denominator 2 end fraction
    Hence, roots are fraction numerator 3 plus square root of 3 over denominator 2 end fraction comma space fraction numerator 3 minus square root of 3 over denominator 2 end fraction
    Question 41
    CBSEENMA10006520
    Wired Faculty App

    Find the values of k for each of the following quadratic equations, so that they have equal roots.
    space 2 straight x squared plus kx plus 3 equals 0

    Solution

    We have,
    space 2 straight x squared plus kx plus 3 equals 0
    Here, straight a equals 2 comma space straight b space equals straight k space and space straight c space equals space 3
    Now,             straight D equals straight b squared minus 4 ac space space space equals space left parenthesis straight k right parenthesis squared minus 4 left parenthesis 2 right parenthesis space left parenthesis 3 right parenthesis space space space equals space straight k squared minus 24
    For equal roots,
                           D = 0
    rightwards double arrow      straight b squared minus 4 ac equals 0
    rightwards double arrow     space straight k squared minus 24 equals 0
    rightwards double arrow            straight k squared equals 24
    rightwards double arrow           straight k equals plus-or-minus square root of 24
    rightwards double arrow           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 42
    CBSEENMA10006521
    Wired Faculty App

    Find the values of k for each of the following quadratic equations, so that they have equal two roots.
    kx (x – 2) + 6 = 0

    Solution

    We have,
    Kx (x – 2) + 6 = 0
    ⇒ Kx2 – 2Kx + 6 = 0
    Here, a = K, b = –2K, c = 6
    Now, D = b2 – 4ac
    ⇒ D = (–2K)2 – 4(K) (6)
    D = 4K2 – 24K
    For equal roots, D = 0
    ⇒ 4K2 – 24K = 0
    ⇒ 4 K (K – 6) = 0
    ⇒ 4K = 0 or K – 6 = 0
    ⇒ K = 0 or K = 6.

    Question 43
    CBSEENMA10006522
    Wired Faculty App

    Is it possible to design a rectangular Mango grove whose length is twice its breadth and the area is 800 m2?  If so, find its length and breadth.

    Solution
    Let the breadth of the rectangular mango grove be x m
    So, length = ‘2’ m
    According to question,
    Area = 800
    ⇒ 2x(x) = 800
    ⇒ 2x2 = 800
    ⇒ x2 = 400
    ⇒ x2 – 400 = 0
    ⇒ x2 + 0x – 400 = 0
    Here, a = 1, b = 0, c = – 400
    D = b2 – 4ac
    = 0 – 4(1) (–400)
    = 1600
    So, the given quadratic equation has real roots (∵ D > 0) and hence it is possible to design rectangular mango grove.
    Now, solving the quadratic equation x2 + 0x – 400 = 0, by quadratic formula, we get,

                         straight x equals fraction numerator negative straight b plus-or-minus square root of straight D squared minus 4 ac end root over denominator 2 straight a end fraction
    rightwards double arrow              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow              straight x space equals space 20 space and space minus 20
    ∵               space space space space straight x equals negative 20 is not possible
    So,              straight x equals 20
    Hence, breadth of the rectangular mango grove is 20 m and length is 40 m.

    Question 44
    CBSEENMA10006523
    Wired Faculty App

    Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
    Solution

    Let the present age of first friend be x years. So, present age of other be (20 - x).
    4 years ago,
    Age of first friend = (x – 4) yrs. and age of second friend = (20 – x – 4) yrs = (16 – x) yrs.
    According to question,
    (x – 4) (16 – x) = 48
    ⇒ 16 x – x2 – 64 + 4x = 48
    ⇒ –x2 + 20x – 112 = 0
    ⇒ x2 – 20x + 112 = 0
    Here, a = 1, b = –20, c = 112
    Now, D = b2 – 4 ac
    = (–20)2 – 4(1) (112) = 400 – 448 = –48
    Since, D < 0
    So, the given quadratic equation has no real roots and hence it is not possible to calculate the present ages.

    Question 45
    CBSEENMA10006524
    Wired Faculty App

    Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find its length and breadth.
    Solution

    Let length of the rectangular park be x m and breadth be y m.
    According to question,
    perimeter = 80 m ⇒ 2(l + b) = 80 m
    ⇒ 2 (x + y) = 80
    ⇒ x + y = 40
    ⇒ y = 40 – x
    i.e., breadth = (40 – x)m
    Now, area = 400
    ⇒ l x b = 400
    ⇒ x(40 – x) = 400
    40x – x2 = 400
    ⇒ x2 – 40x + 400 = 0
    Here, a = 1, b = –40, c = 400
    Now, D = b2 – 4ac
    = (–40)2 – 4(1) (400) = 1600 – 1600 = 0
    Since D = 0
    So, the given quadratic equation has equal roots and hence it is possible to design a rectangular park.
    Now solving the quadratic equation x2 – 40x + 400 = 0 by quadratic formula, we get
    Now,       straight x equals fraction numerator negative straight b plus-or-minus square root of straight D over denominator 2 straight a end fraction space space space equals fraction numerator negative left parenthesis negative 40 right parenthesis plus-or-minus square root of 0 over denominator 2 cross times 1 end fraction equals 40 over 2 equals 20
    Hence, length of the rectangular park (x) = 20 m and breadth = (40 – x) m = 40 – 20 = 20 m.

    Question 46
    CBSEENMA10006525
    Wired Faculty App

    State whether the following is quadratic equation:
    (x – 2)2 (x – 1) = (x – 4) (x + 3)

    Solution

    (x –2)2 (x – 1) = (x – 4) (x + 3)
    ⇒ (x2 + 4 – 4x) (x – 1) = (x – 4) (x + 3)
    ⇒ (x3 + 4x – 4x2 – x2 – 4 + 4x)
    = (x2 + 3x – 4x – 12)
    x3 – 5x2 + 8x – 4 = x2 – x – 12
    x3 – 5x2 – x2 + 8x + x – 4 + 12 = 0
    ⇒ x3 – 6x2 + 9x + 8 = 0
    Since, x3 – 6x2 + 9x + 8 = 0 is a polynomial of degree 3, hence this is not a quadratic equation.

    Question 47
    CBSEENMA10006526
    Wired Faculty App

    State whether the following is quadratic equation:
    (x – 4) (x – 3) = (x – 3) (x2 – 4)

    Solution

    We have,
    (x–4) (x–3) = (x–3) (x2 – 4)
    ⇒ (x – 4) = x2 – 4
    ⇒ x2 – x – 4 + 4 = 0
    ⇒ x2 – x = 0
    Since, x2 – x = 0 is a polynomial of degree 2, hence this is a quadratic equation.

    Question 48
    CBSEENMA10006527
    Wired Faculty App

    State whether the following is quadratic equation:
    square root of 2 straight x squared plus 4 straight x plus 5 square root of 2 plus 3 equals 0

    Solution
    We have,
    square root of 2 straight x squared plus 4 straight x plus 5 square root of 2 plus 3 straight x equals 0 rightwards double arrow space space space space space square root of 2 straight x squared plus 7 straight x plus 5 square root of 2 equals 0
    Since,  square root of 2 straight x squared plus 7 straight x plus 5 square root of 2 equals 0 is a polynomial of degree 2, hence this is a quadratic equation.
    Question 49
    CBSEENMA10006528
    Wired Faculty App

    Write the nature of the roots of the following quadratic equation:
    space space straight x squared minus 1 half straight x minus 4 equals 0.
    Solution

    We have,
    straight x squared minus 1 half straight x minus 4 equals 0
    straight a equals 1 comma space straight b equals fraction numerator negative 1 over denominator 2 end fraction space and space straight c equals space minus 4
                              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    ∵            D > 0
    Hence, roots are real and distinct.

    Question 50
    CBSEENMA10006531
    Wired Faculty App

    Write the nature of the roots of the following quadratic equation:
    3 straight x squared minus 2 straight x plus 1 third equals 0
    Solution
    3 straight x squared minus straight x plus 1 third equals 0
    Here,   straight a equals 3 comma space space straight b space equals space minus 2 space space and space straight c space equals space 1 third
               straight D equals straight b squared minus 4 ac
                  equals left parenthesis negative 2 right parenthesis squared minus 4 left parenthesis 3 right parenthesis open parentheses 1 third close parentheses
                   equals 4 minus 4 space equals space 0
    ∵      D = 0
    Hence, roots are real and equal.
    Question 51
    CBSEENMA10006532
    Wired Faculty App

    Which of the following is quadratic equation:
    space space space space space 2 straight x squared plus 5 straight x equals 7

    Solution

    2x2 + 5x = 7 ⇒ 2x2 + 5x – 1 = 0
    Since 2x2 + 5x – 7 is a quadratic polynomial
    Hence, 2x2 + 5x – 7 = 0 is a quadratic equation.

    Question 52
    CBSEENMA10006533
    Wired Faculty App

    Which of the following is quadratic equation:
      straight x plus 1 over straight x equals 2 semicolon space straight x not equal to 0

    Solution
    space space straight x plus 1 over straight x equals 2
    rightwards double arrow         space space straight x squared plus 1 equals 2 straight x
    rightwards double arrow   straight x squared minus 2 straight x plus 1 equals 0
    Since x2 – 2x + 1 is a quadratic polynomial
    Hence, x2 – 2x + 1 = 0 is a quadratic equation.
    Question 53
    CBSEENMA10006534
    Wired Faculty App

    Which of the following is quadratic equation:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
      

    Solution
    straight x squared minus 1 over straight x squared equals 0
    rightwards double arrow            space space straight x to the power of 4 minus 1 equals 0
    Since x4 – 1 is a polynomial of degree 4, hence this is not a quadratic equation.
    Question 54
    CBSEENMA10006535
    Wired Faculty App

    Which of the following is quadratic equation:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

      

    Solution
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Since straight x squared plus square root of straight x plus 2 is not a polynomial, hence the given equation is not quadratic.
    Question 55
    CBSEENMA10006536
    Wired Faculty App

    Which of the following is quadratic equation:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>


      

    Solution
    straight x squared plus 1 over straight x squared equals 4 straight x squared plus 1 over straight x squared equals 4
    rightwards double arrow           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow        straight x to the power of 4 minus 4 straight x squared plus 1 equals 0
    Since x4 – 4x2 + 1 is a polynomial of degree 4, hence this is not a quadratic equation.
    Question 56
    CBSEENMA10006539
    Wired Faculty App

    Represent the following situation in the form of a quadratic equation:
    The sum of a number and its reciprocal is 13 over 6.

    Solution
    Let the number be x. So, its reciprocal be 1 over straight x.
    According to question,
                 straight x plus 1 over straight x equals 13 over 6
    rightwards double arrow     fraction numerator straight x squared plus 1 over denominator straight x end fraction equals 13 over 6
    rightwards double arrow          6 straight x squared plus 6 equals 13 straight x
    rightwards double arrow         <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Therefore, the number, satisfies the quadratic equation.
    6x2 – 13x + 6 = 0
    which is the required representation of the problems.
    Question 57
    CBSEENMA10006540
    Wired Faculty App

    Represent the following situation in the form of a quadratic equation:
    The sum of two numbers is 60 and their product is 800.

    Solution

    Let the first number be x
    ∴ Other number = (60 – x)
    According to question,
    x (60 – x) = 800
    ⇒ 60x – x2 = 800
    ⇒ x2 – 60x + 800 = 0
    Therefore, the required equation in the form of quadratic equation is
    x2 – 60x + 800 = 0

     

    Question 58
    CBSEENMA10006541
    Wired Faculty App

    Represent the following situation in the form of a quadratic equation:
    The length of a rectangular hall is 3 m more than its breadth. If the area of the hall is 108 m2.

    Solution

    Let the breadth of the rectangular hall be ‘x’ m.
    So, length be (x + 3) m
    According to question,
    Area = 180
    i.e., Length x breadth = 108
    ⇒ x(x + 3) = 108
    ⇒ x2 + 3x = 108
    ⇒ x2 + 3x – 108 = 0
    Therefore, the required representation in the form of quadratic equation be x2 + 3x – 108 = 0.

    Question 59
    CBSEENMA10006542
    Wired Faculty App

    Represent the following situation in the form of a quadratic equation:
    Rohan's mother is 26 years older than him. The product of their ages (in yrs) 3 years from now will be 360. We would like to find Rohan’s present age.

    Solution

    Let the present age of Rohan be x years.
    So, present age of Rohan's mother be (x + 26) years.
    After 3 years
    Rohan’s age = (x + 3) years
    Rohan’s mother age = (x + 26 + 3) years
    = (x + 29) years
    According to question,
    (x + 3) (x + 29) = 360
    ⇒ x2 + 29x + 3x + 87 = 360
    ⇒ x2 + 32x + 87 – 360 = 0
    ⇒ x2 + 32x – 273 = 0
    Therefore, the required representation in the form of quadratic equation
    x2 + 32x – 273 = 0

     
    Question 60
    CBSEENMA10006543
    Wired Faculty App

    Represent the following situation in the form of a quadratic equation:
    The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters.

    Solution

    Let one side (AB) = (x – 4)m
    Other side (BC) = x m
    and hypotenuse = 20 m
    We know,
    AC2 = AB2 + BC2
    ⇒ (20)2 = (x – 4)2 + (x)2
    ⇒ 400 = x2 + 16 – 8x + x2
    ⇒ 400 = 2x2 – 8x + 16
    ⇒ 2x2 – 8x – 384 = 0
    ⇒ 2(x2 – 4x –192) = 0
    ⇒ x2– 4x – 192= 0

    Therefore, the required representation in the form of quadratic equation be x2– 4x –192 = 0.

     
    Question 61
    CBSEENMA10006544
    Wired Faculty App

    Represent the following situation in the form of a quadratic equation:
    The sum of the ages of a son and his father (in years) is 35 and the product of their ages is 150.

    Solution

    Let the present age of son be x years. So, present age of father be (35 - x) years.
    According to question,
    x(35 - x) = 150
    ⇒ 35x – x2 = 150
    ⇒ x2 – 35x +150 = 0
    Therefore, the required representation in the form of quadratic equation be x2 – 35x + 150 = 0

    Question 62
    CBSEENMA10006545
    Wired Faculty App

    Represent the following situation in the form of a quadratic equation:
    The product of Aditya’s age in years, five years ago with his age in years 9 years later is 15.

    Solution

    Let the present age of Aditya’s be x years.
    Aditya’s age five years ago = (x – 5) years
    Aditya’s age nine years later = (x + 9) years
    According to question,
    (x – 5) (x + 9) = 15
    x2 + 9x – 5x – 45 = 15
    x2 + 4x – 60 = 0
    Therefore, the required representation in the form of quadratic equation be x2 + 4x – 60 = 0.

    Question 63
    CBSEENMA10006546
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    space space 2 straight x squared minus 4 straight x plus 3 equals 0

    Solution

      We have,
        2x2 – 4x + 3 = 0
    Here, a = 2, b = – 4, c = 3
    Now, D = b2 – 4ac
    = (–4)2 – 4(2) (3) = 16 – 24 = –8
    Since, D < 0
    Therefore, the given quadratic equation has no real roots.

    Question 64
    CBSEENMA10006548
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    3 straight x squared minus 2 straight x plus 1 third equals 0

    Solution

    We have,
          3 straight x squared minus 2 straight x plus 1 third equals 0
    Here,    straight a equals 3 comma space straight b equals negative 2 comma space straight c equals 1 third
    Now,        
                  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Since, D = 0
    Therefore, the given quadratic equation has equal roots.

    Question 65
    CBSEENMA10006551
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    2 straight x squared minus 3 straight x plus 5 equals 0

    Solution
    We have,
                2 straight x squared minus 3 straight x plus 5 equals 0
    Here,    space space space straight a equals 2 comma space straight b space equals negative 3 comma space straight c space equals 5
    Now,      
                 straight D equals straight b squared minus 4 ac space space space equals space left parenthesis negative 3 right parenthesis squared minus 4 left parenthesis 2 right parenthesis left parenthesis 5 right parenthesis space space space equals 9 space minus 40 space equals space minus 31
    Since,     D < 0
    Therefore, the given quadratic equation has no real roots.
    Question 66
    CBSEENMA10006555
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    3 straight x squared minus 4 square root of 3 straight x plus 4 equals 0

    Solution
    We have,
    3 straight x squared minus 4 square root of 3 straight x plus 4 equals 0
    Here,     straight a equals 3 comma space space space space straight b equals negative 4 square root of 3 comma space space straight c space equals 4
    Now,          space straight D equals straight b squared minus 4 ac space space space space space equals space left parenthesis negative 4 square root of 3 right parenthesis squared minus 4 left parenthesis 3 right parenthesis space left parenthesis 4 right parenthesis
                            equals 48 minus 48 equals 0
    Since,    D = 0
    Therefore, the given quadratic equation has equal roots.
    Question 67
    CBSEENMA10006557
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    2x2 – 6x + 3 = 0
    Here, a = 2, b = –6, c = 3
    Now, D = b2 – 4ac
    = (–6)2 – 4(2) (3) = 36 – 24 = 12
    Since, D > 0
    Therefore, given quadratic equation has real roots.

    Question 68
    CBSEENMA10006558
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    2 square root of 3 straight y squared minus 14 straight y plus 4 square root of 3 equals 0

    Solution
    2 square root of 3 straight y squared minus 14 straight y plus 4 square root of 3 equals 0
    Here,  straight a equals 2 square root of 3 comma space space straight b equals negative 14 comma space straight c equals 4 square root of 3
    Now,     
                  space straight D equals straight b squared minus 4 ac space space space space equals space left parenthesis negative 14 right parenthesis squared minus 4 left parenthesis 2 square root of 3 right parenthesis space left parenthesis 4 square root of 3 right parenthesis space space space space equals space 196 space minus space 96 space equals 100
     Since,  D > 0
    Therefore, given quadratic equation has real roots.
    Question 69
    CBSEENMA10006560
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    space space 4 straight y squared minus 2 straight y plus 1 fourth equals 0

    Solution
    space space 4 straight y squared minus 2 straight y plus 1 fourth equals 0
    Here,      <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Now,               straight D equals straight b squared minus 4 ac
                               equals left parenthesis negative 2 right parenthesis squared minus 4 left parenthesis 4 right parenthesis space open parentheses 1 fourth close parentheses equals space 4 minus 4 space equals space 0
    Since,     D = 0
    Therefore, given quadratic equation has equal roots.
    Question 70
    CBSEENMA10006563
    Wired Faculty App

    Find the discriminant of the following quadratic equation, and hence find the nature of its roots.
    2 straight x squared plus 5 square root of 2 straight x plus 6 equals 0

    Solution

    We have,
               2 straight x squared plus 5 square root of 2 straight x plus 6 equals 0
    Here,             straight a equals 2 comma space space straight b equals 5 square root of 2 comma space straight c equals 6
    Now,              
                           straight D equals straight b squared minus 4 ac space space space space equals space left parenthesis 5 square root of 2 right parenthesis 2 minus 4 left parenthesis 2 right parenthesis space left parenthesis 6 right parenthesis space space space space equals 50 minus 48 space equals 2
    Since,     space space straight D greater than 0
    Therefore, given quadratic equation has real roots.

    Question 71
    CBSEENMA10006564
    Wired Faculty App

    Find the discriminant of the following quadratic equations, and hence find the nature of its roots.
    negative straight x squared plus 2 straight x plus 3 equals 0

    Solution

    –x2 + 2x + 3 = 0
    Here, a = 1, b = 2, c = 3
    Now, D = b2 – 4ac
    = (2)2 –4(–1)(3) = 4 + 12 = 16
    Since, D > 0
    Therefore, given quadratic equation has real roots.

    Question 72
    CBSEENMA10006566
    Wired Faculty App

    Find the discriminant of the following quadratic equations, and hence find the nature of its roots.
    straight x squared plus straight x plus 1 equals 0

    Solution

    x2 + x + 1 = 0
    Here, a = 1, b = 1, c = 1
    Now, D = b2 – 4ac
    = (1)2 – 4(1) (1) = 1 – 4 = –3
    Since, D < 0
    Therefore, given quadratic equation has no real roots.

    Question 73
    CBSEENMA10006568
    Wired Faculty App

    For what value of A, are the roots of the quadratic equation 3x2 + 2kx + 27 = 0 real and equal?

    Solution

    The given quadratic equation is
    3x2 + 2kx + 27 = 0
    Here, a = 3, b = 2k and c = 27
    D = b2 – 4ac = (2k2) – 4 x 3 x 27 = 4k2 – 324
    The given equation will have real and equal roots, if 
    straight D equals 0 space rightwards double arrow space 4 straight k squared minus 324 equals 0 space space space space space space space space space space space space space space space space space space space space space space rightwards double arrow space space 4 straight k squared space equals 324
                   rightwards double arrow straight k squared space equals space 81 space rightwards double arrow space straight k space equals plus-or-minus square root of 81 space equals space plus-or-minus 9 space space Ans. space

    Question 74
    CBSEENMA10006569
    Wired Faculty App

    For what value of A, are the roots of the quadratic equation: kx2 + 4x + 1 = 0 equal and real?

    Solution
    Here, a = k, b = 4, c = 1
    ∴ D = b2 – 4ac = (4)2 – 4k x 1 = 16 – 4k
    Roots are equal and real, if D = 0
    ⇒ 16 – 4k = 0
    ⇒ k = 4 
    Question 75
    CBSEENMA10006570
    Wired Faculty App

    For what value of A, does (k – 12)x2 + 2 (k – 12)x + 2 = 0 have equal roots?

    Solution

    Here, a = k – 12, b = 2 (k – 12), c = 2
    ∴ D = b2 – 4ac = [2(k– 12)]2
    – 4(k – 12) x 2
    = 4 (k – 12)2 – 8 (k– 12)
    Roots are equal, if D = 0
    ⇒ 4 (k – 12) 2 – 8 (k – 12) = 0
    ⇒ 4(k – 12)(k – 12 – 2) = 0
    ⇒ (k – 12) (k – 14) = 0
    ⇒ k = 12 or 14
    But k = 12 does not satisfy the eqn.
    k = 14 Ans.

    Question 76
    CBSEENMA10006574
    Wired Faculty App

    For what value of A, does the equation 9x2 + 3kx + 4 = 0 have equal roots?

    Solution

    Here a = 9, b = 3k, c = 4
    ∴ D = b2 – 4ac = (3k)2 – 4 x 9 x 4 = 9k2 – 144
    Roots are equal, if D = 0
    ⇒ 9k2 – 144 = 0
    ⇒ 9k2 = 144
    ⇒ 9k2 – 144 = 0
    ⇒ k2 – 16 = 0
    ⇒ (k)2 – (4)2 = 0
    ⇒ (k + 4) (k – 4) = 0
    ⇒ k + 4 = 0 or, k – 4 = 0
    ⇒ k = 4

    Question 77
    CBSEENMA10006578
    Wired Faculty App

    If (–5) is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p(x2 + x) + k = 0 has equal roots, then find the values of p and A.

    Solution

    ∵ (–5) is a root of the quadratic equation
    ∴ 2x2 + px – 15 = 0
    2(–5)2 + p. (–5) – 15 = 0
    ⇒ 50 – 5p – 15 = 0
    ⇒ –5p + 35= 0
    ⇒ –5p = –35
    ⇒ P = 7
    Now. the quadratic equation 7(x2 + x) + k = 0
    i.e. 7x2 + 7x + k = 0 has equal roots.
    ∴      Its discriminant  straight D equals left parenthesis 7 right parenthesis squared minus 4 cross times 7 cross times straight k space is space zero
    rightwards double arrow            <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow              straight k equals 49 over 28 equals 7 over 4
    Hence,   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 78
    CBSEENMA10006582
    Wired Faculty App

    If one of the roots of the quadratic 2x2 + px – 4 = 0 is 4. Write value of p.

    Solution

    Let the roots of the quadratic equation be α and β.
    We have,
    2x2 + px – 4 = 0, then
    Product of the roots = fraction numerator negative 4 over denominator 2 end fraction equals negative 2
    rightwards double arrow       straight alpha. space straight beta equals negative 2
    But        straight alpha equals 4
    rightwards double arrow space space space space 4 space left parenthesis straight beta right parenthesis space equals space minus 2
    rightwards double arrow        <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Sum of the roots = fraction numerator negative straight p over denominator 2 end fraction
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    space rightwards double arrow space space space space space space space space space space space space space 4 minus 1 half equals fraction numerator negative straight p over denominator 2 end fraction space rightwards double arrow space space space space space space space space space space space space space space space space fraction numerator negative straight p over denominator 2 end fraction space equals space 7 over 2 space rightwards double arrow space space space space space space space space space space space space space space space space space space space space straight p space equals space minus 7

    Question 79
    CBSEENMA10006586
    Wired Faculty App

    Find the discriminant of the quadratic equation.
           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    The given quadratic equation is
    space space space space space space space space space space space space space space space space 3 square root of 3 straight x squared plus 10 straight x plus square root of 3 space equals space 0
    Here,   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Discriminant      = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
                              = left parenthesis 10 right parenthesis squared minus 4 cross times 3 square root of 3 cross times square root of 3
                             = 100 - 36
                             = 64 Ans. 

    Sponsor Area

    Question 80
    CBSEENMA10006589
    Wired Faculty App

    Show that x = – 3 is a solution of x2 + 6x + 9 = 0.

    Solution

    The given quadratic equation is
    x2 + 6x + 9 = 0 Putting a = – 3, we get
    L.H.S. = (– 3)2 + 6. (– 3) + 9
    = 9 – 18 + 9
    = 19 – 18 = 0 = R.H.S.
    Hence, x = – 3 is a solution of x2 + 6x + 9 = 0 Proved.

    Question 81
    CBSEENMA10006592
    Wired Faculty App

    Show that x = – 3 is a solution of 2x2 + 5x – 3 = 0. 

    Solution

    The given quadratic equation is
    2x2 + 5x – 3 = 0 Putting a = – 3, we get
    L.H.S. = 2x2 + 5x – 3
    = 2 (–3)2 + 5 (– 3) – 3
    = 2 x 9 – 15 – 3
    = 18 – 15 – 3 = 15 – 15 = 0 = R.H.S.
    Hence, x = – 3 is a solution of 2x2 + 5x – 3 = 0 Proved.

    Question 82
    CBSEENMA10006595
    Wired Faculty App

    Show that x = – 2 is a solution of 3x2 + 13x + 14 = 0.

    Solution

    The given quadratic equation is
    3x2 + 13x + 14 = 0
    Putting a = – 2, we get
    L.H.S. = 3.(–2)2 + 13.(–2) + 14
    = 3 x 4 – 26 + 14
    = 12 – 26 + 14
    = 26 – 26 = 0 = R.H.S.
    Hence, x = – 2 is a solution of 3x2 + 13x + 14 = 0 Proved.

     
    Question 83
    CBSEENMA10006599
    Wired Faculty App

    What is the descriminant of the following equation:
    2x2 – 3x + 1 = 0

    Solution

    We have,
    a = 2, b = – 3 and c = 1
    Now, D = b2 – 4ac
    = (– 3)2 – 4(2) (1) = 9 – 8 = 1
    Hence, Descriminant (D) = 1.

    Question 84
    CBSEENMA10006608
    Wired Faculty App

    Find the values of K for which the given equation Kx2 – 6x – 2 = 0 has real roots.

    Solution

    We have,
        Kx squared minus 6 straight x minus 2 equals 0
    Here,  a = K,  b = -6  and c = -2
    ∴                       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    For real roots:
                           space space straight D greater or equal than 0
     rightwards double arrow      <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    space rightwards double arrow space space space space space space space space 8 straight K greater or equal than negative 36
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 85
    CBSEENMA10006612
    Wired Faculty App

    Find the values of K for which the equation x2 + 5Kx + 16 = 0 has no real roots.

    Solution

    We have,
     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Here,  a = 1;   b = 5K and c = 16
    ∴               straight D equals straight b squared minus 4 ac space space space space equals space left parenthesis 5 straight K right parenthesis squared minus 4 left parenthesis 1 right parenthesis left parenthesis 16 right parenthesis space space space space equals space 25 straight K squared minus 64
    The given equation will have no real roots, if
                            straight D less than 0
    rightwards double arrow          <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow           left parenthesis 5 straight K right parenthesis squared minus left parenthesis 8 right parenthesis squared less than 0
    rightwards double arrow      left parenthesis 5 straight K plus 8 right parenthesis space left parenthesis 5 straight K minus 8 right parenthesis space less than space 0
    rightwards double arrow                      <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 86
    CBSEENMA10006614
    Wired Faculty App

    Write the values of k for which the quadratic equation x2 – kx + 9 = 0 has equal roots.

    Solution

    Here, a = 1,
    b = k and c = 9
    For equal roots D = 0
    ⇒ b2 – 4ac = 0
    ⇒ (–k)2 – 4(1) (9) = 0
    ⇒ k2 – 36 = 0
    ⇒ k = ± 6.

    Question 87
    CBSEENMA10006615
    Wired Faculty App

    What is the nature of roots of the quadratic equation 4x2 – 12x – 9 = 0?

    Solution

    Here, a = 4, b = –12 and c = –9
    D = b2 – 4ac
    = (–12)2 – 4 (4) (–9)
    = 144 + 144 = 288
    Since D > 0, therefore, roots of the given equation are real and unequal. Ans.

    Question 88
    CBSEENMA10006616
    Wired Faculty App

    Is x = –2 a solution of the equation x2 – 2x + 8 = 0?

    Solution

    Let  p(–2) = x2 – 2x + 8
    p(–2) = (–2)2 –2 (–2) + 8
    = 4 + 4 + 8
    = 8 + 8 = 16
    ∴ x = –2 is not a solution of the given equation

    Question 89
    CBSEENMA10006617
    Wired Faculty App

    Write the nature of roots of quadratic equation 4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0.

    Solution

    We have
                space space space straight a equals 4 comma space straight b equals 4 square root of 3 space and space straight c equals 3
    Now  
                straight D equals straight b squared minus 4 ac space space space equals space left parenthesis 4 square root of 3 right parenthesis squared minus 4 left parenthesis 4 right parenthesis left parenthesis 3 right parenthesis space space space equals space 48 space minus 48 space equals space 0 because space space straight D space space equals space 0 space
    Hence, roots are real and equal.

    Question 100
    CBSEENMA10006640
    Wired Faculty App

    It is possible to find two consecutive integers whose product is 72. If so, find the integers.

    Solution

    Solution not provided.
    Ans. Yes;   8, 9

    Question 105
    CBSEENMA10006649
    Wired Faculty App

    Is it possible to find a and b. Whose sum is 15 and the sum of their reciprocals 1 over straight a space and space 1 over straight b is 3 over 10. If so, find them.

    Solution

    Solution not provided.
    Ans. Yes, 5, 10 or 10, 5

    Question 108
    CBSEENMA10006653
    Wired Faculty App

    Is it possible to find the two numbers whose sum is 15 and sum of their reciprocals is 3 over 10. If so, find the numbers.

    Solution

    Solution not provided.
    Ans. Yes, 10 and 5.

    Question 109
    CBSEENMA10006654
    Wired Faculty App

    The sum of a number and its positive square root is <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> Find the number.

    Solution

    Solution not provided.
    Ans. 1 over 25

    Question 110
    CBSEENMA10006655
    Wired Faculty App

    Solve the following by factorization method:
    x2 – 2ax + a2 – b2 = 0 

    Solution

    Solution not provided.
    Ans. a - b,  a + b

    Question 111
    CBSEENMA10006656
    Wired Faculty App

    Solve the following by factorization method:
     x2 – 4ax + 4a2 – b2 = 0.

    Solution

    Solution not provided.
    Ans. 2a - b,  2a + b

    Question 114
    CBSEENMA10006660
    Wired Faculty App

    Solve the following quadratic equation by factorization method:
    a2b2x2 + b2x – a2x – 1 = 0. 

    Solution

    Solution not provided.
    Ans. fraction numerator negative 1 over denominator straight a squared end fraction comma space 1 over straight b squared

    Question 115
    CBSEENMA10006661
    Wired Faculty App

    Solve the following quadratic equation by factorization method:
    a2b2x2 + b2x – a2x – 1 = 0. 

    Solution

    Solution not provided.
    Ans.  1 comma space minus open parentheses fraction numerator straight a minus straight b over denominator straight a plus straight b end fraction close parentheses

    Question 117
    CBSEENMA10006663
    Wired Faculty App

    Solve the following quadratic equation by factorization method:
    4x2 + 4bx – (a2 – b2) = 0.

    Solution

    Solution not provided.
    Ans. fraction numerator straight a minus straight b over denominator 2 end fraction comma space space minus fraction numerator straight a plus straight b over denominator 2 end fraction

    Question 119
    CBSEENMA10006665
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    2 straight x squared minus 7 straight x plus 3 equals 0

    Solution

    Solution not provided.
    Ans.  space space straight x equals 3 comma space 1 half

    Sponsor Area

    Question 120
    CBSEENMA10006666
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.  straight x equals fraction numerator negative 1 plus-or-minus square root of 33 over denominator 8 end fraction

    Question 121
    CBSEENMA10006667
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0

    Solution

    Solution not provided.
    Ans.  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 122
    CBSEENMA10006668
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.  straight x equals fraction numerator negative 1 plus-or-minus square root of 33 over denominator 4 end fraction

    Question 123
    CBSEENMA10006669
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
        4 straight x squared minus 20 straight x plus 25 equals 0

    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 124
    CBSEENMA10006670
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    3 straight x squared plus 2 straight x minus 1 equals 0
        

    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 125
    CBSEENMA10006671
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
        2 straight y squared plus straight y minus 1 equals 0
        

    Solution

    Solution not provided.
    Ans.  straight y equals fraction numerator negative 1 plus-or-minus square root of 10 over denominator 4 end fraction 

    Question 126
    CBSEENMA10006672
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    3 straight x squared minus 5 straight x minus 2 equals 0
        
        

    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 127
    CBSEENMA10006673
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    9 straight x squared plus 7 straight x minus 2 equals 0

        
        

    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 128
    CBSEENMA10006674
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    space space 6 straight y squared plus straight y minus 2 equals 0


        
        

    Solution

    Solution not provided.
    Ans.   straight y equals 1 half comma space fraction numerator negative 2 over denominator 3 end fraction

    Question 129
    CBSEENMA10006675
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    4 straight x squared plus 6 straight x plus 2 equals 0



        
        

    Solution

    Solution not provided.
    Ans.   straight x equals fraction numerator negative 1 over denominator 2 end fraction comma space minus 1

    Question 130
    CBSEENMA10006676
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    6 straight x squared plus 21 straight x plus 15 space equals space 0




        
        

    Solution

    Solution not provided.
    Ans.   straight x equals negative 1 comma space space fraction numerator negative 5 over denominator 2 end fraction

    Question 131
    CBSEENMA10006678
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>





        
        

    Solution

    Solution not provided.
    Ans.   straight y equals 2 comma space 5 over 2

    Question 132
    CBSEENMA10006679
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>






        
        

    Solution

    Solution not provided.
    Ans.   space space space space space space straight y equals fraction numerator negative 5 plus-or-minus 2 square root of 3 over denominator 5 end fraction

    Question 133
    CBSEENMA10006680
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>







        
        

    Solution

    Solution not provided.
    Ans.   straight x equals negative 20 comma space space straight x equals 15

    Question 134
    CBSEENMA10006681
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    space space space space 2 straight x squared minus 3 straight x plus 1 equals 0








        
        

    Solution

    Solution not provided.
    Ans.   straight x equals 1 comma space 1 half

    Question 135
    CBSEENMA10006682
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    space space space 2 straight x squared minus 3 straight x plus 1 equals 0










        
        

    Solution

    Solution not provided.
    Ans.   straight x equals 1 comma space 1 half

    Question 136
    CBSEENMA10006684
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>











        
        

    Solution

    Solution not provided.
    Ans. space space straight x equals fraction numerator negative 2 straight b over denominator 3 straight a end fraction comma space fraction numerator negative 2 straight b over denominator straight a end fraction

    Question 137
    CBSEENMA10006685
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    straight x squared minus 8 straight x plus 16 equals 0












        
        

    Solution

    Solution not provided.
    Ans.  x = 4,  4

    Question 138
    CBSEENMA10006686
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    straight x squared minus 8 straight x minus 20 space equals space 0













        
        

    Solution

    Solution not provided.
    Ans.  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 139
    CBSEENMA10006687
    Wired Faculty App

    Solve the following quadratic equation by the method of completing the square.
    space 2 straight x squared plus 7 straight x minus 4 equals 0.














        
        

    Solution

    Solution not provided.
    Ans.  straight x equals 1 half comma space minus 4

    Question 140
    CBSEENMA10006688
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.  x = a + b,  a - b

    Question 141
    CBSEENMA10006689
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    straight y squared minus 4 straight y minus 1 equals 0

    Solution

    Solution not provided.
    Ans.  straight y equals 2 plus-or-minus square root of 5

    Question 142
    CBSEENMA10006691
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    straight y squared plus 1 half straight y minus 1 equals 0

    Solution

    Solution not provided.
    Ans.  straight y equals fraction numerator negative 1 plus-or-minus square root of 17 over denominator 4 end fraction

    Question 143
    CBSEENMA10006692
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    9 straight x squared minus 6 straight a squared straight x plus left parenthesis straight a to the power of 4 minus straight b to the power of 4 right parenthesis space equals space 0

    Solution

    Solution not provided.
    Ans.  straight x equals fraction numerator straight a squared plus-or-minus straight b squared over denominator 3 end fraction

    Question 144
    CBSEENMA10006694
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    space straight x squared plus 5 straight x plus 5 space equals space 0

    Solution

    Solution not provided.
    Ans.   straight x equals fraction numerator negative 5 plus-or-minus square root of 5 over denominator 2 end fraction

    Question 145
    CBSEENMA10006695
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    2 straight x squared plus straight x minus 1 equals 0

    Solution

    Solution not provided.
    Ans.   straight x equals 1 half comma space minus 1

    Question 146
    CBSEENMA10006696
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 147
    CBSEENMA10006697
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    left parenthesis straight y plus 4 right parenthesis space left parenthesis straight y plus 5 right parenthesis space equals space 3 left parenthesis straight y plus 1 right parenthesis left parenthesis straight y plus 2 right parenthesis plus 2

    Solution

    Solution not provided.
    Ans.   y = 0.6

    Question 148
    CBSEENMA10006698
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    straight y squared plus 6 straight y plus 9 equals 0

    Solution

    Solution not provided.
    Ans.   y = -3,  -3

    Question 149
    CBSEENMA10006699
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    fraction numerator 2 straight x over denominator straight x minus 3 end fraction plus fraction numerator 1 over denominator 2 straight x plus 3 end fraction plus fraction numerator 3 straight x plus 9 over denominator left parenthesis straight x minus 3 right parenthesis space left parenthesis 2 straight x plus 3 right parenthesis end fraction space equals space 0 space open square brackets straight x not equal to 3 comma space space space straight x not equal to negative 3 over 2 close square brackets

    Solution

    Solution not provided.
    Ans.  x = -1

    Question 150
    CBSEENMA10006700
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.  y = 2,  -5

    Question 151
    CBSEENMA10006701
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    3 straight x squared minus 14 straight x minus 5 equals 0

    Solution

    Solution not provided.
    Ans.  straight x equals fraction numerator negative 1 over denominator 3 end fraction comma space 5

    Question 152
    CBSEENMA10006705
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    square root of 3 straight y squared plus 11 straight y plus 6 square root of 3 space equals space 0

    Solution

    Solution not provided.
    Ans.  straight y equals negative fraction numerator 2 over denominator square root of 3 end fraction comma space space space minus 3 square root of 3

    Question 153
    CBSEENMA10006707
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    square root of 3 straight y squared plus 10 straight y plus 7 square root of 3 space equals space 0

    Solution

    Solution not provided.
    Ans.  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 154
    CBSEENMA10006709
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    fraction numerator 5 straight y plus 1 over denominator 2 straight y plus 3 end fraction plus fraction numerator 2 straight y plus 3 over denominator 5 straight y plus 1 end fraction equals 5 over 2 comma space space space space straight y space not equal to negative 3 over 2 comma space space space straight y not equal to fraction numerator negative 1 over denominator 5 end fraction

    Solution

    Solution not provided.
    Ans.  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 155
    CBSEENMA10006710
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    space space 3 plus 7 over straight x minus 6 over straight x squared equals 0 semicolon space space space straight x not equal to 0

    Solution

    Solution not provided.
    Ans.  straight x equals 2 over 3 comma space minus 3

    Question 156
    CBSEENMA10006712
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.  space space space straight y equals negative 4 over 3 comma space fraction numerator negative 6 over denominator 7 end fraction

    Question 157
    CBSEENMA10006713
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    straight x minus 8 square root of straight x minus 20 equals 0.

    Solution

    Solution not provided.
    Ans.  x = 4, 100

    Question 158
    CBSEENMA10006714
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    straight y squared plus 2 square root of 2 straight y minus 6 equals 0

    Solution

    Solution not provided.
    Ans.  straight y equals square root of 2 comma space minus 3 square root of 2

    Question 159
    CBSEENMA10006716
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.   x = 5,  10

    Question 160
    CBSEENMA10006719
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    straight y squared minus 12 straight y plus 35 equals 0.

    Solution

    Solution not provided.
    Ans. y = 5, 7

    Question 161
    CBSEENMA10006720
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.  x = 750, -1000

    Question 162
    CBSEENMA10006721
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    9 straight x squared plus 12 straight x plus 4 equals 0

    Solution

    Solution not provided.
    Ans.  straight x equals fraction numerator negative 2 over denominator 3 end fraction comma space space fraction numerator negative 2 over denominator 3 end fraction

    Question 163
    CBSEENMA10006722
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    straight x squared plus straight x minus 156 equals 0

    Solution

    Solution not provided.
    Ans.    x = 12, -13

    Question 164
    CBSEENMA10006723
    Wired Faculty App

    Find the roots of the quadratic equation by using quadratic formula:
    space space space space straight y squared equals 41 straight y minus 400.

    Solution

    Solution not provided.
    Ans.    x = 16, 25

    Question 165
    CBSEENMA10006724
    Wired Faculty App

    Use quadratic formula to solve the following equation for x:
    abx2 + (b2 – ac) x – bc = 0.

    Solution

    Solution not provided.
    Ans.    straight x equals straight c over straight b comma space space straight x equals fraction numerator negative straight b over denominator straight a end fraction

    Question 166
    CBSEENMA10006725
    Wired Faculty App

    Use quadratic formula to solve the following equation for x:
    9x2 – 9 (a + b)x + (2a2 + 5ab + 2b2) = 0.

    Solution

    Solution not provided.
    Ans.  fraction numerator 2 straight a plus straight b over denominator 3 end fraction comma space space fraction numerator straight a plus 2 straight b over denominator 3 end fraction   

    Question 167
    CBSEENMA10006726
    Wired Faculty App

    Use quadratic formula to solve the following equation for x:
    a2x2 + (a2 – b2)x – b2 = 0.

    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>  

    Question 168
    CBSEENMA10006729
    Wired Faculty App

    A two digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.

    Solution
    Let the tens digit be x. Then, the units digits equals space 18 over straight x
       ∴       Number equals space 10 straight x plus 18 over straight x
    and Number obtained by interchanging the digits
                          space space equals 10 cross times 18 over straight x plus straight x
    ∴    open parentheses 10 straight x plus 18 over straight x close parentheses minus open parentheses 10 cross times 18 over straight x plus straight x close parentheses space equals space 63
    rightwards double arrow        space space space 10 straight x plus 18 over straight x minus 180 over straight x minus straight x equals 63
    rightwards double arrow              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow              left parenthesis straight x minus 9 right parenthesis space left parenthesis straight x plus 2 right parenthesis space equals space 0
    rightwards double arrow                    straight x equals 9 space space or space space straight x space equals space minus 2
    So,                            straight x equals 9.
    Hence, the required number equals 10 cross times 9 plus 18 over 9 equals 92.
    Question 169
    CBSEENMA10006731
    Wired Faculty App

    Sum of the areas of two squares is 260 m2. If the difference of their perimeters is 24 m, then find the sides of the two squares. 

    Solution

    Let side of bigger square is x m. And, side of smaller square is y m.
    According to given condition,
    x2 + y2 = 260 ...(i)
    And 4x – 4y = 24
    ⇒ 4(x – y) = 24
    ⇒ x – y = 6
    ⇒ x = 6 + y ...(ii)
    Putting the value of (ii) in (i), we get
    (6 + y) 2 + y2 = 260
    ⇒ 36 + y2 + 12y + y2 = 260
    ⇒ 2y2 + 12y – 224 = 0
    ⇒ y2 + 6y – 112 = 0
    ⇒ y2 + 14y – 5y – 112 = 0
    ⇒ y(y + 14) –8(y + 14) = 0
    ⇒ (y – 8) (y + 14) = 0
    ⇒ y–8 = 0, y + 14 = 0
    ⇒ y = 8, y = – 14
    Putting the value of y in (ii), we get
    x = 6 + y
    = 6 + 8 = 14.
    Hence, sides of squares are 14 cm and 8 cm.

    Question 170
    CBSEENMA10006733
    Wired Faculty App

    The sum of the squares of two consecutive odd numbers is 394. Find the numbers. 

    Solution
    Let two consecutive odd numbers are (2n – 1) and (2n + 1).Then
                        <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow     4 straight n squared minus 4 straight n plus 1 plus 4 straight n squared plus 4 straight n plus 1 equals 394
    rightwards double arrow             <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                     straight n equals plus-or-minus square root of 49 space equals space plus-or-minus 7
    When n = 7, then two consecutive odd numbers are:
    2 x 7 – 1 = 13 and 2 x 7 + 1 = 15 i.e., 13 and 15 Ans.
    When n = –7, then two consecutive odd numbers are:
    2 x (–7) – 1 = –15 and 2 x (–7) + 1 = –13 i.e., –15 and –13 Ans.
    Question 171
    CBSEENMA10006734
    Wired Faculty App

    The denominator of a fraction exceeds its numerator by 2. If one is added to both numerator and denominator, the difference between the new and the original fractions is 1/21. Find the original fractions.

    Solution
    Let numerator of the fraction be x
    So, denominator = x + 2
    Hence, fraction (original) = space space fraction numerator straight x over denominator straight x plus 2 end fraction
    If 1 is added to both numerator and denominator then,
                       Numerator  = x + 1
    and           denominator  = x + 2 + 1 = x + 3
       Hence,        fraction  = fraction numerator straight x plus 1 over denominator straight x plus 3 end fraction
    According to the given condition,
                             space fraction numerator straight x plus 1 over denominator straight x plus 3 end fraction minus fraction numerator straight x over denominator straight x plus 2 end fraction equals 1 over 21
    rightwards double arrow     fraction numerator left parenthesis straight x plus 1 right parenthesis left parenthesis straight x plus 2 right parenthesis minus straight x left parenthesis straight x plus 3 right parenthesis over denominator left parenthesis straight x plus 3 right parenthesis left parenthesis straight x plus 2 right parenthesis end fraction equals 1 over 21
    rightwards double arrow       fraction numerator left parenthesis straight x squared plus 2 straight x plus straight x plus 2 right parenthesis minus straight x squared minus 3 straight x over denominator straight x squared plus 2 straight x plus 3 straight x plus 6 end fraction equals 1 over 21
    rightwards double arrow         fraction numerator straight x squared plus 3 straight x plus 2 minus straight x squared minus 3 straight x over denominator straight x squared plus 5 straight x plus 6 end fraction equals 1 over 21
    rightwards double arrow                  fraction numerator 2 over denominator straight x squared plus 5 straight x plus 6 end fraction equals 1 over 21
    rightwards double arrow space space space space space space space space x squared plus 5 x plus 6 space equals space 42 rightwards double arrow space space space space space space space space x squared plus 5 x minus 36 space equals space 0 rightwards double arrow space space space space space space space space x squared plus 9 x minus 4 x minus 36 space space equals space 0 rightwards double arrow space space space space space space space space x left parenthesis x plus 9 right parenthesis minus 4 left parenthesis x plus 9 right parenthesis space space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space left parenthesis x minus 4 right parenthesis space left parenthesis x plus 9 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space x space minus space 4 space equals space 0
    or                           straight x plus 9 space equals space 0
           rightwards double arrow                     x = 4
    or                              x = -9
         x = -9 is not possible
        Therefore,    x  = 4
        Now, numerator = x = 4
    and denominator  = x + 2 = 6
      So, required fractions are 4 over 6 space or space space 2 over 3.
    Question 172
    CBSEENMA10006736
    Wired Faculty App

    A two-digit number is four times the sum and three times the product of its digits. Find the number.

    Solution

    Let the digits at tens and units place of the number be x and y respectively. Then, Number = 10x + 7
    It is given that,
    ⇒ 10x + y = 4(x + y)
    and 10x + y = 3xy
    ⇒ 6x – 3y = 0 and 10x + y = 3y
    ⇒ y – 2x and 10x + y = 3xy
    ⇒ 10x + 2x = 3x X 2x
    ⇒ 6x2 – 12x = 0
    ⇒ 6x (x – 2) = 0
    ⇒ x = 0 or x = 2
    Since the given number is a two-digit number. So, its tens digit cannot be zero.
    ∴ x = 2
    ⇒ y = 2 x 2 = 4 [∵ = 2x]
    Hence,
    required number = 10x+y = 10 x 2 + 4 = 24.1

    Question 173
    CBSEENMA10006738
    Wired Faculty App

    O Girl! Out of a group of swans, space 7 over 2 times the square root of the number are playing on the shore of a tank. The two remaining ones are playing, with amorous fight, in the water. What is the total number of swans?

    Solution
    Let the total number of swans be x. Then, Number of swans playing on the shore of the tank <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
               Remaining swans = 2
                Now,
    ∴                                straight x equals 7 over 2 square root of straight x plus 2
    rightwards double arrow         straight x minus 7 over 2 square root of straight x minus 2 equals 0
    Let                            space space space square root of straight x space equals space 4
    ∴                                    straight x equals straight y squared
    rightwards double arrow          straight y squared minus 7 over 2 straight y minus 2 equals 0 comma where straight y squared equals straight x
    rightwards double arrow         2 straight y squared minus 7 straight y minus 4 equals 0
    rightwards double arrow       2 straight y squared minus 8 straight y plus straight y minus 4 equals 0
    rightwards double arrow     2 straight y left parenthesis straight y minus 4 right parenthesis space plus space left parenthesis straight y minus 4 right parenthesis space space equals space 0
    rightwards double arrow             left parenthesis straight y minus 4 right parenthesis space left parenthesis 2 straight y plus 1 right parenthesis space space equals space 0
    rightwards double arrow                  straight y equals 4 space or space straight y space equals space minus 1 half
    rightwards double arrow                             straight y equals 4
    rightwards double arrow                     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                        straight x equals 16.
    Hence, the total number of swans is 16.
    Question 174
    CBSEENMA10006741
    Wired Faculty App

    Out of a number of Saras birds, one-fourth the number are moving about in lotus plants; <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> 7 times the square root of the number move on a hill; 56 birds remain in vakula trees. What is the total number of birds? (Mahavira) 

    Solution
    Let the total number of birds be x
    Number of birds moving in lotus plant <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Number of birds moving on a hill
                              equals straight x over 9 plus straight x over 4 plus 7 square root of straight x
    Number of birds in vakula trees  = 56
    According to the given condition,
     ∴   Total number of birds
                            equals straight x over 4 plus straight x over 9 plus straight x over 4 plus 7 square root of straight x plus 56 equals space straight x over 2 plus straight x over 9 plus 7 square root of straight x plus 56
    ∴        straight x equals straight x over 2 plus straight x over 9 plus 7 square root of straight x plus 56
    rightwards double arrow    straight x minus straight x over 2 minus straight x over 9 minus 56 space equals space 7 square root of straight x
    rightwards double arrow space 18 minus 9 straight x minus 2 straight x minus 18 cross times 56 space equals space 18 cross times 7 square root of straight x
    rightwards double arrow                7 straight x minus 18 cross times 56 space equals space 18 cross times 7 square root of straight x
    rightwards double arrow space space space space space space space space space space space space space space space space straight x space minus 144 space equals space 18 square root of straight x
    rightwards double arrow                 left parenthesis straight x minus 144 right parenthesis squared space equals space left parenthesis 18 square root of straight x right parenthesis squared
    rightwards double arrow       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow space space space space space straight x squared minus 612 straight x plus 20736 space equals space 0 rightwards double arrow space space space straight x squared minus 36 straight x minus 576 straight x plus 20736 space equals space 0 rightwards double arrow space straight x left parenthesis straight x minus 3 right parenthesis space minus space 576 left parenthesis straight x minus 36 right parenthesis space equals space 0 therefore space space space space space space space left parenthesis straight x minus 36 right parenthesis space left parenthesis straight x minus 576 right parenthesis space equals space 0
    ∴               space space straight x equals 36 space space or space space straight x space equals space 576
    But x ≠ 36
    ∴ x = 576
    ∴ Total number of Saras birds = 576.
    Question 175
    CBSEENMA10006742
    Wired Faculty App

    The angry Arjun carried some arrows for fighting with Bheeshm. With half the arrows, he cut down the arrows thrown by Bheeshm on him and with six other arrows, he killed the rath driver of Bheeshm. With one arrow each, he knocked down respectively the rath, flag and the bow of Bheeshm. Finally, with one more than four times the square root of arrows he laid Bheeshm unconscious of on arrow bed. Find the total number of arrows Arjun had.

    Solution
    Let the total number of arrows carried by Arjun = x.
    Given : Number of arrows used to cut arrows of Bheesm space equals space Half space of space total space arrow space equals space straight x over 2
    Number of arrows used to kill the rath driver = 6 Number of other arrows used to knock down rath, flag and bow = 1 + 1 + 1= 3
    The number of arrows, with which he laid Bheeshm unconscious = 4 square root of straight x plus 1
    According to given condition,
      rightwards double arrow                     space space space straight x equals straight x over 2 plus 6 plus 3 plus 4 square root of straight x plus 1
    rightwards double arrow                          <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                     straight x minus 8 square root of straight x minus 20 space equals space 0
    rightwards double arrow space space space straight x minus 10 square root of straight x plus 2 square root of straight x minus 20 space equals space 0
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow space space space space space space space space space space space square root of straight x space equals space 10 space or space square root of straight x space equals space minus 2 space space but space square root of straight x space can apostrophe straight t space be space negative
    rightwards double arrow space space space space square root of straight x space equals space 10 space space rightwards double arrow space straight x space equals space 100
    Thus, the total number of arrows Arjun had = 100. Ans.
    Question 176
    CBSEENMA10006744
    Wired Faculty App

    A motorboat whose speed in still water is 5 km/h, takes 1 hour more to go 12 km upstream than to return downstream to the same spot. Find the speed of the stream. 

    Solution

    Let the speed of the stream be x km/hr.
    Then, speed downstream = (5 + x) km/hr.
    And, speed upstream = (5 – x) km/hr.
    Now, Time taken by the boat to cover 12 km upstream = fraction numerator 12 over denominator 5 plus straight x end fraction hrs. space
    And, Time taken by the boat to cover 12 km downstream = fraction numerator 12 over denominator 5 plus straight x end fraction hrs.
    According to given condition:
                          fraction numerator 12 over denominator 5 minus straight x end fraction equals fraction numerator 12 over denominator 5 plus straight x end fraction plus 1
    rightwards double arrow       fraction numerator 12 over denominator 5 minus straight x end fraction minus fraction numerator 12 over denominator 5 plus straight x end fraction equals 1
    rightwards double arrow space space space space space space space space space space space space space space fraction numerator 12 left parenthesis 5 plus straight x right parenthesis minus 12 left parenthesis 5 minus straight x right parenthesis over denominator left parenthesis 5 minus straight x right parenthesis space left parenthesis 5 plus straight x right parenthesis end fraction equals 1 rightwards double arrow space space space space space space space space space space space space space space space fraction numerator 60 plus 12 straight x minus 60 plus 12 straight x over denominator 25 minus straight x squared end fraction equals 1
    rightwards double arrow                      24 straight x equals 25 minus straight x squared
    rightwards double arrow       space straight x squared plus 24 straight x minus 25 equals 0            
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Hence, speed of stream  = 1 km/hr.           

    Question 177
    CBSEENMA10006745
    Wired Faculty App

    A plane left 30 minutes later than the schedule time and in order to reach its destination 1500 km away in time it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.

    Solution
    Let the usual speed of the plane be x km/hr. Then,
    Time taken to cover 1500 km with the usual speed <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Time taken to cover 1500 km with the speed of (x + 250) km/hr = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
          According to given condition,
                                <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow           1500 over straight x minus fraction numerator 1500 over denominator straight x plus 250 end fraction equals 1 half
    space space rightwards double arrow space space space space fraction numerator 1500 straight x plus 1500 cross times 250 minus 1500 straight x over denominator straight x left parenthesis straight x plus 250 right parenthesis end fraction equals 1 half space space rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space fraction numerator 1500 cross times 250 over denominator straight x squared plus 250 straight x end fraction equals 1 half
    rightwards double arrow                                       750000 space equals space straight x squared plus 250 straight x
    rightwards double arrow                <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow space space space straight x squared plus 1000 straight x minus 750 straight x minus 750000 space equals space 0 rightwards double arrow space space straight x left parenthesis straight x plus 1000 right parenthesis minus 750 left parenthesis straight x plus 1000 right parenthesis space equals space 0
    rightwards double arrow                 <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    ∵   Speed cannot be negative.
    Hence, usual speed of the plane is 750 km/hr.

    Question 178
    CBSEENMA10006747
    Wired Faculty App

    Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after two hours, they are 50 km apart, find the average speed of each train.

    Solution
    Let the speed of the second train be x km hr. Then, the speed of the first train is (x + 5) km/hr.
    Let O be the position of the railway station from which the two trains leave.

    Distance travelled by the first train in 2 hours
    = OA = Speed x Time
    = 2 (x + 5) km
    Distance travelled by the second train in 2 hours
    = OB = Speed x Time
    = 2x km
    By using pythagoras theorem, we have,
    AB2 = OA2 + OB2
    ⇒ 502 = {2(x + 5)}2+ {2x}2
    ⇒ 2500 = 4(x + 5)2 + 4x2
    ⇒ 8x2 + 40x – 2400 = 0
    ⇒ x2 + 5x – 300 = 0
    ⇒ x2 + 20x – 15x – 300 = 0
    ⇒ x (x + 20) – 15 (x + 20) = 0
    ⇒ (x + 20) (x – 15) = 0
    ⇒ x = –20 or x = 15
    ⇒ x = 15
    [∵ cannot be negative]
    Hence, the speed of the second train is 15 km/hr and the speed of the first train is 20 km/hr.



    Question 179
    CBSEENMA10006749
    Wired Faculty App

    A fast train takes 3 hours less than a slow train for a journey of 600 km. If the speed of the slow train is 10 km/hr less than that of the fast train, find the speeds of the two trains.

    Solution

    Let the speed of the fast train = x km/hr
    ⇒ The speed of slow train = (x – 10) km/hr
    Time taken by the fast train to cover 600 km <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> and Time taken by the slow train to cover 600 km 
                              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    According to given condition,
                      space space space fraction numerator 600 over denominator straight x minus 10 end fraction minus 600 over straight x equals 3
    rightwards double arrow space space space fraction numerator 600 straight x minus 600 left parenthesis straight x minus 10 right parenthesis over denominator left parenthesis straight x minus 10 right parenthesis straight x end fraction equals 3 rightwards double arrow space space space space space space space space space space 3 left parenthesis straight x squared minus 10 straight x right parenthesis space equals space 600 straight x minus 600 straight x plus 6000 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space straight x squared minus 10 straight x space equals space 2200 rightwards double arrow space space space left parenthesis straight x minus 50 right parenthesis space left parenthesis straight x plus 40 right parenthesis space equals space 0 semicolon space space space space space straight x space equals space 50 space space or space straight x space equals space minus 40
    Neglecting x = -40, we get:  x = 50 and x - 10 = 50 - 10 = 40
    rightwards double arrow    Speed of fast train = 50 km/hr and  speed of slow train  = 40 km/hr.

    Question 180
    CBSEENMA10006751
    Wired Faculty App

    In a flight of 600 km an aircraft was slowed down due to bad weather. Its average speed for the trip was reduced by 200 km/hr and the time of flight increased by 30 minutes. Find the duration of flight.

    Solution
    Let original speed of the aircraft be x km/hr. Then,
    New speed = (x - 200) km/hr
    Duration of flight at original speed
                           space space equals space open parentheses 600 over straight x close parentheses hr.
    Duration of flight at reduced speed
                            space space equals open parentheses fraction numerator 600 over denominator straight x minus 200 end fraction close parentheses hr.
    According to given condition, 
                       fraction numerator 600 over denominator straight x minus 200 end fraction equals 600 over straight x plus 1 half
    space rightwards double arrow space space space space space space space space space space space space space space space space space space space space fraction numerator 600 over denominator straight x minus 200 end fraction minus 600 over straight x equals 1 half space rightwards double arrow space space space space space space space space space space space space space fraction numerator 600 straight x minus 600 left parenthesis straight x minus 200 right parenthesis over denominator straight x left parenthesis straight x minus 200 right parenthesis end fraction equals 1 half space rightwards double arrow space space space space space space space space space space space space space space space space space space space fraction numerator 600 straight x minus 600 straight x plus 120000 over denominator straight x squared minus 200 straight x end fraction equals 1 half
    space space space space rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space fraction numerator 120000 over denominator straight x squared minus 200 straight x end fraction equals 1 half
    rightwards double arrow space space space space space space space straight x squared minus 200 straight x minus 240000 space equals space 0 rightwards double arrow space space space straight x squared minus 600 straight x plus 400 straight x minus 240000 space equals space 0 rightwards double arrow space space space straight x left parenthesis straight x minus 600 right parenthesis space plus space 400 left parenthesis straight x minus 600 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space left parenthesis straight x plus 400 right parenthesis space left parenthesis straight x minus 600 right parenthesis space equals space 0 rightwards double arrow space space space space space space straight x plus 400 space equals space 0 space space space space space space space space straight x minus 600 space equals space 0 rightwards double arrow space space space space space space space space straight x space equals space minus 400 space space space space space space space space space space space space space space space rightwards double arrow space space straight x space equals space 600 because space space space space space straight x space equals space 400 space is space rejected.
    So, the original speed of the aircraft was 600 km/hr
    Hence, Duration of flight
                           space space equals space open parentheses 600 over straight x close parentheses hr space space equals space open parentheses 600 over 600 close parentheses hr space equals space 1 space hr.
    Question 181
    CBSEENMA10006752
    Wired Faculty App

    Seven years ago Varun’s age was five times the square of Swati’s age. Three years hence Swati’s age will be two fifth of Varun’s age. Find their present ages.

    Solution

    Seven years ago, let Swati’s age be x years.
    Then, seven years ago Varun’s age was 5x2 years.
    ∴ Swati’s present age = (x + 7) years
    Varun’s present age = (5x2 + 7) years
    Three years hence,
    Swati’s age = (x + 7 + 3) years
    = (x + 10) years
    and Varun’s age = (5x2 + 7 + 3) years
    = (5x2 + 10) years
    According to given condition,
    ∴               straight x plus 10 space equals space 2 over 5 left parenthesis 5 straight x squared plus 10 right parenthesis
    rightwards double arrow space space space space space space space space space space space space space space space space straight x plus 10 space equals space 2 straight x squared plus 4 rightwards double arrow space space space space space space space space 2 straight x squared minus straight x minus 6 space equals space 0 rightwards double arrow space space space 2 straight x squared minus 4 straight x plus 3 straight x minus 6 space equals space 0 rightwards double arrow space space space 2 straight x left parenthesis straight x minus 2 right parenthesis space plus space 3 left parenthesis straight x minus 2 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space left parenthesis 2 straight x plus 3 right parenthesis thin space left parenthesis straight x minus 2 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space straight x minus 2 space equals space 0 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left square bracket because space space space space 2 straight x plus 3 not equal to 0 space as space straight x greater than 0 right square bracket rightwards double arrow space space space space space space space space space space space space space space space space space space space space space straight x space equals space 2 space space space space space space space space space space space space space space space space space
    Hence, Swati's present age = (2 + 7) years  = 9 years
      Varun's present age = space left parenthesis 5 cross times 2 squared plus 7 right parenthesis space years space equals space 27 space years.

    Question 182
    CBSEENMA10006753
    Wired Faculty App

    The sum of ages of a father and his son is 45 years. Five years ago, the product of their ages (in years) was 124. Determine their present ages.

    Solution

    Let the present age of father be x years. Then,
    Son’s present age = (45 – x) years
    Five years ago,
    Age of Father = (x – 5) years
    and Age of Son = (45 – x – 5) years = (40 – x) years
    According to given condition,
    (x – 5) (40 – x) = 124
    ⇒ 40x – x2 – 200 + 5x = 124
    ⇒ x2 – 45x + 324 = 0
    ⇒ x2 – 36x – 9x + 324 = 0
    ⇒ x (x – 36) – 9 (x – 36) – 0
    ⇒ (x - 9) (x - 36) = 0
    ⇒x = 9 or x = 36
    When x = 36, we have
    Father’s present age = 36 years
    Son’s present age = 9 years
    When x = 9, we have
    Father’s present age = 9 years
    Son’s present age = 36 years
    Clearly, this is not possible
    Hence, Father’s present age = 36 years and Son’s present age = 9 years.

    Question 183
    CBSEENMA10006755
    Wired Faculty App

    One year ago, the father was 8 times as old as his son. Now his age is the square of his son’s age. Find their present ages.

    Solution

    Let present age of the son be x years
    ∴ Present age of the father = x2 years
    one year ago,
    Age of the son = (x – 1) years
    and Age of the father = (x2 – 1) years
    According to the given condition,
    x2 – 1 = 8(x – 1)
    ⇒ x2 – 1 – 8x + 8 = 0
    x2 – 8x + 7 = 0
    ⇒ (x – 1) (x– 7) = 0
    ⇒ x – 1 = 0,  x – 7 = 0
    i.e., x = 1,  x = 7
    When x = 1, age of son = age of father, which is impossible
    ∴ x = 1 is rejected.
    ∴ x = 7
    Thus present age of son = 7 years
    and present age of father = 49 years.

    Question 184
    CBSEENMA10006757
    Wired Faculty App

    Two years ago, a man's age was three times the square of his son's age. In three years time, his age will be four times his son's age. Find their present ages.

    Solution

    Let present age of son = x years
    Two years ago, Age of son = (x – 2) years
    Age of man = 3(x – 2)2
    ∴ Man’s present age = 3(x – 2)2 + 2
    = 3(x2 – 4x + 4) + 2
    = 3x2 – 12x + 14
    Age of man = 3(x – 2)2
    ∴ Man’s present age = 3(x – 2)2 + 2
    = 3(x2 – 4x + 4) + 2
    = 3x2 – 12x + 14
    After 3 year
    The age of son  = (x + 3) years
    Age of man  equals space left parenthesis 3 straight x squared minus 12 straight x plus 14 right parenthesis plus 3 equals space left parenthesis 3 straight x squared minus 12 straight x plus 17 right parenthesis space years
    According to given condition,
                    3 straight x squared minus 12 straight x plus 17 space equals space 4 left parenthesis straight x plus 3 right parenthesis
    rightwards double arrow space space space space space space space space space space 3 straight x squared minus 12 straight x plus 17 space equals space 4 straight x plus 12 rightwards double arrow space space space space space space space space space space space 3 straight x squared minus 16 straight x plus 5 space space space equals space space space 0 rightwards double arrow space space space space space space space space space space left parenthesis straight x space minus 5 right parenthesis space left parenthesis 3 straight x minus 1 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space straight x space equals space 5 space space or space straight x space equals space 1 third
    Since, <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    ∴    The present age of man
                                 equals space 3 straight x squared minus 12 straight x plus 14 equals space 3 cross times 5 squared minus 12 cross times 5 space plus space 14 equals space 29 space years

     And, the present age of son = x = 5 years. Ans.
    Question 185
    CBSEENMA10006759
    Wired Faculty App

    The age of a Father is twice the square of the age of his son. Eight years hence the age of the father will be 4 years more than three times the age of his son. Find their present ages. 

    Solution

    Let the present ages of son be x years.
    Then,        Age of father = 2x2
    After 8 years    Age of son =  (x + 8) yrs.
    And              Age of father  = (2x2+8) yrs.
    According to given condition
                          2 straight x squared plus 8 space equals space 3 left parenthesis straight x plus 8 right parenthesis plus 4
    rightwards double arrow                 2 straight x squared plus 8 space equals space 3 straight x plus 24 plus 4
    rightwards double arrow space space space space 2 straight x squared minus 3 straight x minus 20 space equals space 0 rightwards double arrow space space space space 2 straight x squared minus 8 straight x plus 5 straight x minus 20 space equals space 0 rightwards double arrow space space space space 2 straight x left parenthesis straight x minus 4 right parenthesis plus 5 left parenthesis straight x minus 4 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space left parenthesis 2 straight x plus 5 right parenthesis space left parenthesis straight x minus 4 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space 2 straight x plus 5 space equals space 0 comma space space space space space space space space space space straight x space minus space 4 space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space 2 straight x space equals space minus 5 comma space space space space space space space straight x space equals space 4 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space straight x space equals space fraction numerator negative 5 over denominator 2 end fraction left parenthesis Rejected right parenthesis
    Hence,  present age of son = 4 years
    And, present age of father = 2(4)2 = 32 yrs.

    Question 186
    CBSEENMA10006760
    Wired Faculty App

    The hypotenuse of a right angled triangle is 6 metres more than twice the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle.

    Solution
    Let the shortest side of the triangle be x m. Then,
    Hypotenuse = (2x + 6) m
    and third side = (2x + 6 – 2) m
    = (2x + 4) m
    According to Pythagoras theorem, we have
    (2x + 6)2 = x2 + (2x + 4)2
    ⇒ 4x2 + 24x + 36 = x2 + 4x2 + 16x + 16
    ⇒ 24x - 16x + 36 - 16 = x2
    ⇒ 8x + 20 = x2
    ⇒ x2 – 8x – 20 = 0
    ⇒ x2–10x + 2x - 20 = 0
    ⇒ x(x– 10) + 2(x – 10) = 0
    ⇒ (x – 10) (x + 2) = 0
    ⇒ x – 10 = 0 or x + 2 = 0
    ⇒ x = 10 or x = –2
    As length of the side cannot be negative, it is rejected.
    ∴ 2x + 4 = 20 + 4 = 24 and 2x + 6 = 20 + 6 = 26
    Thus, the side of the triangle are 10 m, 24 m and 26 m.
    Question 187
    CBSEENMA10006763
    Wired Faculty App

    The hypotenuse of a right triangle is 1 m less than twice the shortest side. If the third side is 1 m more than the shortest side, find the sides of the triangle.

    Solution

    Let the shortest side (BC) = x m
    Then, hypotenuse (AC) = (2x – 1) m
    and third side (AB) = (x + 1) m
    Now in right ΔABC, We have
    AC2 = AB2 + BC2 [By Pythagoras Theorem)
    ⇒ (2x – 1)2 = (x + 1)2 + (x)2
    ⇒ 4x2 + 1 – 4x = x2 + 1 + 2x + x2
    ⇒ 4x2 + 1 – 4x = 2x2 + 2x + 1
    ⇒ 2x2– 6x = 0
    ⇒ 2x(x – 3) = 0
    ⇒ 2x = 0
    or x – 3 = 0
    x = 0
    or x = 3
    Since x = 0 is not possible.
    So, x = 3
    Hence, required sides of the triangle are
    AB = x + 1 = 4 m.
    BC = x = 3 m
    and AC = 2x – 1 = 5 m.

    Question 188
    CBSEENMA10006765
    Wired Faculty App

    The hypotenuse of a right triangle is 25 cm. The difference between the lengths of the other two sides of the triangle is 5 cm. Find the lengths of these sides.

    Solution
    Let the length of the longer side (AB) = x cm Then, length of shorter side (BC) = (x – 5) cm and hypotenuse (AC) = 25 cm

    In right triangle ABC, We have
    AC2 = AB2 + BC2 [By Pythagoras theorem)
    ⇒ (25)2 = (x)2 + (x – 5)2
    ⇒ 625 = x2 + x2 + 25 – 10x
    ⇒ 625 = 2x2 – 10x + 25
    ⇒ 2x2 – 10x – 600 = 0
    ⇒ x2 – 5x – 300 = 0
    ⇒ x2 – 20x + 15x – 300 = 0
    ⇒ x(x – 20) + 15(x – 20) = 0
    ⇒ (x + 15) (x – 20) = 0
    ⇒ x + 15 = 0
    or x – 20 = 0
    ⇒  x = – 15
    or x = 20
    Since x = –15 is not possible
    Therefore, x = 20
    Hence, required sides of the triangle are
    BC = x – 5 = 20 – 5 = 15 cm
    and AB = x = 20 cm.



    Question 189
    CBSEENMA10006767
    Wired Faculty App

    The length of the hypotenuse of a right triangle exceeds the base by 2 cm and exceeds twice the length of altitude by 1 cm. Find each side.

    Solution

    Let the base (BC) of a right triangle be x cm and altitude (AB) be y cm.
    Then, according to question, Hypotenuse (AC) = (x + 2) cm ...(i)
    and hypotenuse (AC) = (2y + 1) cm ...(ii)
    Comparing (i) and (ii), we get
    x + 2 = 2y + 1
    ⇒ 2y = x + 2 – 1
    ⇒ 2y = x + 1
    rightwards double arrow          space straight y equals fraction numerator straight x plus 1 over denominator 2 end fraction

    Now,
                 <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Now, in ΔABC, we have
    AC squared equals AB squared plus BC squared
    [Using Pythagoras theorem]
    rightwards double arrow space space space space space space space space space space left parenthesis straight x plus 2 right parenthesis squared space equals space open parentheses fraction numerator straight x plus 1 over denominator 2 end fraction close parentheses squared plus straight x squared
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    space rightwards double arrow space space 4 straight x squared plus 16 straight x plus 16 space equals space 5 straight x squared plus 2 straight x plus 1 space rightwards double arrow space space space space space space space space space space space space space space space straight x squared minus 14 straight x minus 15 space equals space 0 space rightwards double arrow space space space space space space space space space space space straight x squared minus 15 straight x plus straight x minus 15 space equals space 0 space rightwards double arrow space space space space space straight x left parenthesis straight x minus 15 right parenthesis plus 1 left parenthesis straight x minus 15 right parenthesis space equals space 0 space rightwards double arrow space space space space space space space space space space left parenthesis straight x plus 1 right parenthesis thin space left parenthesis straight x minus 15 right parenthesis space equals 0 space rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space straight x plus 1 space equals space 0 space or space space space space space space space space space space space space space space space space space space space space space space straight x minus 15 space equals space 0 space space space space space space space rightwards double arrow space space space space space space space space space space space space space space space space space space space space space x space equals space minus 1 space space space space space space space rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space straight x space equals space 15
              x = -1 is not possible
              Therefore,               x = 15
               Now, requried sides are
                                              BC = x = 15 cm
                                              AC = x + 2 = 17 cm
    and                                     AB = fraction numerator straight x plus 1 over denominator 2 end fraction equals 8 space cm.

    Question 190
    CBSEENMA10006768
    Wired Faculty App

    Manisha wishes to fit three rods together in the shape of a right triangle. The hypotenuse is to be 2 cm longer than the base and 4 cm longer than the altitude. What should be the length of the rods?

    Solution
    Let the base of the triangle be x cm and altitude be y cm.

    Then, according to question,
    Hypotenuse (AC)= (x + 2) cm ...(i)
    Hypotenuse (AC)= (y + 4) cm ...(ii)
    Comparing (i) and (ii), we get
    x + 2 = y + 4
    ⇒ y = x – 2
    ⇒ AB = (x – 2) cm
    Now in right triangle ABC, We have
    AC2 = AB2 + BC2 [Using Pythagoras theorem]
    (x + 2)2 = (x – 2)2 + (x)2
    ⇒ x2 + 4 + 4x = x2 + 4 – 4x + x2
    ⇒ x2 + 4a + 4 = 2x2 – 4x + 4
    ⇒ x2 – 8x = 0
    ⇒ x (x – 8) = 0
    ⇒ A = 0
    or x – 8 = 0
    ⇒ x = 0
    or x = 8
    x = 0 is not possible
    Therefore, x = 8 cm
    Now required sides be
    BC = x = 8 cm
    AB = x – 2 = 8 – 2 = 6 cm
    and AC = (x + 2) = (8 + 2)
    = 10 cm.

    Question 191
    CBSEENMA10006769
    Wired Faculty App

    The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm. Find the other two sides.

    Solution

    Let the base (BC) of the right triangle = x cm
    So, altitude (AB) = (x – 7) cm
    And hypotenuse (AC) = 13 cm

    According to Pythagoras theorem,
    AC2 = AB2 + BC2
    ⇒ (13)2 = (x – 7)2 + (x)2
    ⇒ 169 = x2 + 49 – 14x + x2
    ⇒ 169 = 2x2 –14x + 49
    ⇒ 2x2 – 14x – 120 = 0
    ⇒ x2 – 7x – 60 = 0
    ⇒ x2 – 12x + 5x – 60 = 0
    ⇒ x(x – 12) + 5(x – 12) = 0
    ⇒ (x + 5) (x – 12) = 0
    ⇒ x + 5 = 0
    or x – 12 = 0
    ⇒ x = – 5
    or x = 12
    Since side of triangle is never negative
    So, x = 12
    Now required sides of the triangle are
    AB = x – 7
    = 12 – 7 = 5 cm and BC = x = 12 cm.

     

    Question 192
    CBSEENMA10006770
    Wired Faculty App

    The sum of the areas two squares is 640 m2. If the difference in their perimeter be 64 m, Find the sides of the two squares.

    Solution
    Let the sides of the squares be x m and y m. Then,
    Area of the first square = x2 m
    Area of the second square = y2 m
    Perimeter of the first square = 4x m
    and Perimeter of the second square = 4y m
    According to the given condition,
    x2 + y2 = 640 ...(i)
    and 4x – 4y = 64 or x – y = 16 ...(ii)
    From (ii), y = x – 16 ...(iii)
    Substituting the value of y in (i), we get
    x2 + (x – 16)2 = 640
    ⇒ x2 + x2 + 256 – 32x = 640
    ⇒ 2x2 – 32x + 256 = 640
    ⇒ 2x2 – 32x – 384 = 0
    ⇒ x2 – 16x – 192 = 0
    ⇒ x2 – 24x + 8x – 192 = 0
    ⇒ x (x – 24) +8 (x – 24) = 0
    ⇒ (x + 8) (x – 24) = 0
    x = 24 or x = –8
    ⇒ x = –8 rejected as the side of a square cannot be negative.
    Hence, side of the first square,
    x = 24 m
    and side of the second square,
    y = (24 – 16) m ...[Using (iii)]
    = 8 m.
    Question 193
    CBSEENMA10006771
    Wired Faculty App

    If twice the area of a smaller square is subtracted from the area of a larger square, the result is 14 sq cm. However, if twice the area of larger square is added to three times the area of the smaller square, the result is 203 sq. cm. Find the sides of the two squares.

    Solution
    Let the side of the smaller square be x cm and side of the larger square be y cm. Then,
    According to the given conditions, we have
    y2 – 2x2 = 14 ...(i)
    and 2y2 + 3x2 = 203 ...(ii)
    Substituting y2 = 14 + 2x2
    From (i) in (ii), we get
    2(14 + 2x2) + 3x2= 203
    ⇒ 28 + 4x2 + 3x2 = 203
    ⇒ 7x2 = 175
    ⇒ x2 = 25
    ⇒ x = ±5
    ∴ x = 5 [x = –5 is rejected]
    From (i), y2 –2x2 = 14
    ⇒ y2 – 2(5)2 = 14
    ⇒ y2 – 50 = 14
    ⇒ y2 = 64
    ⇒ y = ±8
    ⇒ y = 8 [y = –8 is rejected]
    Hence, side of smaller square = 5 cm
    and side of larger square = 8 cm.
    Question 194
    CBSEENMA10006772
    Wired Faculty App

    The hypotenuse of a right triangle is 3 square root of 5 space cm. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be 15 cm. Find the length of each side.

    Solution

             <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    If the smaller side is tripled and the larger side be doubled, the new hypotenuse is 15 cm. Then,
    (3x)2 + (2y)2 = 152
    ⇒ 9x2 + 4y2 = 225 ...(ii)
    From equation (i), we get y2 = 45 – x2
    Putting y2 = 45 – x2 in equation (ii), we get
    9x2 + 4 (45 – x2) = 225
    ⇒ 5x2 +180 = 225
    ⇒ 5x2 = 45
    ⇒ x2 = 9
    ⇒ x = ±3
    But, length of a side cannot be negative.
    Therefore, x = 3.
    Putting x = 3 in (i), we get
    9 + y2 = 45 ⇒ y2 = 36 ⇒ y = 6
    Hence, the length of the smaller side is 3 cm and the length of the larger side is 6 cm.

    Question 195
    CBSEENMA10006773
    Wired Faculty App

    A farmer wishes to grow a 100 m2 rectangular vegetable garden. Since he has with the only 30 m barbed wire, he fences three sides of the rectangular garden letting compound wall of his house act as the four the side-fence. Find the dimension of his garden.

    Solution
    Let the length of one side be x meters and other side by y meters. Then,
    x + y + x = 30 ...(i)
    ⇒ y = 30 – 2x
    ∴ Area of the vegetable garden = 100 m2
    ⇒  xy = 100

    ⇒ xy = 100
    ⇒ x (30 – 2x) = 100
    ⇒ 30x – 2x2 = 100
    ⇒ 15x – x2 = 50
    ⇒ x2 – 15x + 50 = 0
    ⇒ x2 – 10x – 5x + 50 = 0
    ⇒ (x – 10) (x – 5) = 0
    ⇒ x = 5, 10
    When x = 5, we have
    y = 30 – 2 x 5 = 20
    When x = 10, we have
    y = 30 – 2 x 10= 10
    Hence, the dimensions of the vegetable garden are
    5 m x 20 m    or       10 m x 10 m.


    Question 196
    CBSEENMA10006774
    Wired Faculty App

    There is a square field whose side is 44 m. A square flower bed is prepared in its centre leaving a gravel path all round the flower bed. The total cost of laying the flower bed and gravelling the path at Rs. 2.75 and Rs. 1.50 per square metre, respectively, is Rs. 4904. Find the width of the gravel path.

    Solution

    Let the width of the gravel = x metres. Then,
    Each side of the square flower bed
    = (44 – 2x) metres.
    Now, Area of the square field
    = 44 x 44 = 1936 m2
    and Area of the flower bed
    = (44 – 2x)2 m2
    ∴ Area of the gravel path
    = Area of the field – Area of the flower bed
    = 1936 – (44 – 2x)2
    = 1936 – (1936 – 176x +4x2)
    = (176x – 4x2) m2

    Cost of laying the flower bed
    = (Area of the flower bed) (Rate per sq. m)
    equals left parenthesis 44 minus 2 straight x right parenthesis squared cross times 275 over 100 equals 11 over 4 left parenthesis 44 minus 2 straight x right parenthesis squared space equals space 11 left parenthesis 22 minus straight x right parenthesis squared
    Cost of gravelling the path
    = (Area of the path) x (Rate per sq. m)
    = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    It is given that the total cost of laying the flower bed and gravelling the path is Rs. 4904.
    ∴ 11 (22 – x)2 + 6 (44x – x2) = 4904
    ⇒ 11(484 – 44x + x)2 + (264x – 6x2) = 4904
    ⇒ 5x2 – 220x + 5324 = 4908
    5x2 – 220x + 420 = 0
    ⇒ x2 – 44x + 84 = 0
    ⇒ x2 – 42x – 2x + 84 = 0
    ⇒ x (x – 42) – 2 (x – 42) = 0
    ⇒ (x – 2) (x – 42) = 0
    ⇒ x = 2 or x = 42
    But, x ≠ 42, as the side of the square is 44 m.
    Therefore, x = 2.
    Hence, the width of the gravel path is 2 metres.



     

    Question 197
    CBSEENMA10006779
    Wired Faculty App

    Two pipes running together can fill a cistern in space space 3 1 over 13 space minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe would fill the cistern.

    Solution

    Suppose the time taken by the faster pipe is x minutes.
    ∴ Time taken by the slower pipe = (x + 3) minutes
    Now,
    Portion of cistern filled by the faster pipe <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> and portion of cistern filled by the slower pipe = space space fraction numerator 1 over denominator straight x plus 3 end fraction and portion of the cistern filled by the both in 1 minute
        equals 1 over straight x plus fraction numerator 1 over denominator straight x plus 3 end fraction equals space fraction numerator straight x plus 3 plus straight x over denominator straight x left parenthesis straight x plus 3 right parenthesis end fraction equals fraction numerator 2 straight x plus 3 over denominator straight x left parenthesis 2 straight x plus 3 right parenthesis end fraction space... space left parenthesis straight i right parenthesis
    It is given that,
    Portion of the cistern filled by both 1 minute equals 13 over 40        ...(ii)
    Comparing (i) and (ii), we get
                            fraction numerator 2 straight x plus 3 over denominator straight x left parenthesis straight x plus 3 right parenthesis end fraction space equals space 13 over 40
    rightwards double arrow                         space fraction numerator 2 straight x plus 3 over denominator straight x squared plus 3 straight x end fraction equals 13 over 40
    rightwards double arrow                  40 left parenthesis 2 straight x plus 3 right parenthesis space equals space 13 left parenthesis straight x squared plus 3 straight x right parenthesis
    rightwards double arrow                       80 straight x plus 120 space equals space 13 straight x squared plus 39 straight x
    rightwards double arrow                13 straight x squared minus 41 straight x minus 120 space equals space 0
    rightwards double arrow space space 13 straight x squared minus 65 straight x plus 24 straight x minus 120 space equals space 0
    space rightwards double arrow space 13 straight x left parenthesis straight x minus 5 right parenthesis space plus space 24 left parenthesis straight x minus 5 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space left parenthesis 13 straight x plus 24 right parenthesis space left parenthesis straight x minus 5 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space 13 straight x plus 24 space equals space 0 space space space space space space space or space straight x minus 5 space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space 13 straight x space equals space minus 24 space space space rightwards double arrow space space space straight x space equals space 5 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space straight x equals fraction numerator negative 24 over denominator 13 end fraction

    (which is rejected)  Hence, time taken by the faster pipe = x = 5 minutes and time taken by the slower pipe = (x + 3) = 5 + 3 = 8 minutes.


    Question 198
    CBSEENMA10006782
    Wired Faculty App

    A person on tour has Rs. 360 for his expenses. If he extends his tour for 4 days, he has to cut down his daily expenses by Rs. 3. Find the original duration of the tour.

    Solution
    Let the original duration of the tour be x days.
    Total expenditure on tour  = Rs. 360
    ∴     Expenditure per day  = Rs. 360 over straight x
    Duration of the extended tour = (x + 4) days
    ∴ Expenditure per day according to new schedule
                                                   = Rs. fraction numerator 360 over denominator straight x plus 4 end fraction
    According to given condition,
    ∴                      360 over straight x minus fraction numerator 360 over denominator straight x plus 4 end fraction equals 3
    space rightwards double arrow space space fraction numerator 360 left parenthesis straight x plus 4 right parenthesis minus 360 straight x over denominator straight x left parenthesis straight x plus 4 right parenthesis end fraction equals 3 space rightwards double arrow space fraction numerator 360 straight x plus 1440 minus 360 straight x over denominator straight x left parenthesis straight x plus 4 right parenthesis end fraction equals 3 space rightwards double arrow space space space space space space space space space space space space space space space fraction numerator 1440 over denominator straight x squared plus 4 straight x end fraction space equals space 3
    rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space straight x squared plus 4 straight x space equals space 480 rightwards double arrow space space space space space space space space space space space space straight x squared plus 4 straight x minus 480 space equals space 0 rightwards double arrow space space space straight x squared plus 24 straight x minus 20 straight x minus 480 space equals space 0 rightwards double arrow space space straight x left parenthesis straight x plus 24 right parenthesis space minus 20 left parenthesis straight x plus 24 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space left parenthesis straight x space minus space 20 right parenthesis space left parenthesis straight x space plus space 24 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space straight x minus 20 space equals space 0 space space or space straight x space plus space 24 space equals 0 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space straight x space equals space 20 space space or space straight x equals negative 24
    But, the number of days cannot be negative.
    So, x = 20.
    Hence, the original duration of the tour was of 20 days.
    Question 199
    CBSEENMA10006784
    Wired Faculty App

    Rs. 6500 were divided equally among a certain number of persons. Had there been 15 more persons, each would have got Rs. 30 less. Find the original number of persons.

    Solution
    Let the original number of persons be x. Then,
    Share of each person = Rs. 6500 over straight x
    If the number of persons is increased by 15. Then,
    New share of each person = Rs. fraction numerator 6500 over denominator straight x plus 15 end fraction
    According to given condition,
    ∴              6500 over straight x minus fraction numerator 6500 over denominator straight x plus 15 end fraction equals 30
    space rightwards double arrow space space space space fraction numerator 6500 left parenthesis straight x plus 15 right parenthesis minus 6500 straight x over denominator straight x left parenthesis straight x plus 15 right parenthesis end fraction equals 30 space rightwards double arrow space space space space space space space space space space space space space space space space fraction numerator 6500 cross times 15 over denominator straight x left parenthesis straight x plus 15 right parenthesis end fraction space equals space 30 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space fraction numerator 3250 over denominator straight x left parenthesis straight x plus 15 right parenthesis end fraction space equals 1 space rightwards double arrow space space space space space space space space space space space space space space space space space space space straight x squared plus 15 straight x space equals space 3250 space space space space space space space space rightwards double arrow space space space space space space space space space space space space straight x squared plus 15 straight x minus 3250 space equals space 0
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    (which is rejected) Hence, the original number of persons = 50.
    Question 200
    CBSEENMA10006786
    Wired Faculty App

    A shopkeeper buys a number of books for Rs. 80. If he had bought 4 more books for the same amount, each book would have cost Rs. 1 less. How many books did he buy?

    Solution

    Let the number of books bought be x. Then,
    Cost of x books = Rs. 80
    rightwards double arrow         Cost of one book = Rs. open parentheses 80 over straight x close parentheses
    If the number of books bought is x + 4, then
    Cost of one book  = Rs. space open parentheses fraction numerator 80 over denominator straight x plus 4 end fraction close parentheses
    According to given condition,
    ∴                  80 over straight x minus fraction numerator 80 over denominator straight x plus 4 end fraction equals 1
    rightwards double arrow            space space 80 open parentheses 1 over straight x minus fraction numerator 1 over denominator straight x plus 4 end fraction close parentheses space equals space 1
    rightwards double arrow space space space space space space space space space space 80 open curly brackets fraction numerator straight x plus 4 minus straight x over denominator straight x left parenthesis straight x plus 4 right parenthesis end fraction close curly brackets equals 1
    rightwards double arrow                          fraction numerator 320 over denominator straight x squared plus 4 straight x end fraction equals 1
    rightwards double arrow                       straight x squared plus 4 straight x equals 320
    rightwards double arrow             straight x squared plus 4 straight x minus 320 space equals space 0
    rightwards double arrow space space space straight x squared plus 20 straight x minus 16 straight x minus 320 space equals space 0
    rightwards double arrow     straight x left parenthesis straight x plus 20 right parenthesis minus 16 left parenthesis straight x plus 20 right parenthesis space equals 0
    rightwards double arrow space space space space space space space space space space space space space space space space space space space space left parenthesis straight x plus 20 right parenthesis space left parenthesis straight x minus 16 right parenthesis space equals space 0
    rightwards double arrow                                space straight x equals negative 20
    or                                   straight x equals 16
    rightwards double arrow                                  straight x equals 16
    [∵ x cannot be negative]
    Hence, the number of books is 16.

     
    Question 201
    CBSEENMA10006788
    Wired Faculty App

    A takes 6 days less than the time taken by B to finish a piece of work. If both A and B together can finish it in 4 days, find the time taken by B to finish the work.

    Solution

    Suppose B alone takes x days to finish the work. Then, A alone can finish it in (x - 6) days.
    Now, (A’s one day’s work) + (B’s one day’s work)
    equals 1 over straight x plus fraction numerator 1 over denominator straight x minus 6 end fraction
    and   space space space left parenthesis straight A plus straight B right parenthesis apostrophe straight s space one space day space work space equals space 1 fourth
    ∴                1 over straight x plus fraction numerator 1 over denominator straight x minus 6 end fraction equals 1 fourth
    rightwards double arrow                fraction numerator straight x minus 6 plus straight x over denominator straight x left parenthesis straight x plus 6 right parenthesis end fraction equals 1 fourth
    rightwards double arrow                  fraction numerator 2 straight x minus 6 over denominator straight x squared minus 6 straight x end fraction equals 1 fourth
    rightwards double arrow                 8 straight x minus 24 space equals space straight x squared minus 6 straight x
    rightwards double arrow space space space space space space space space space space space space space space space space space straight x squared minus 14 straight x plus 24 equals 0 rightwards double arrow space space space space space space space straight x squared minus 12 straight x minus 2 straight x plus 24 space equals space 0 rightwards double arrow space space space space space space space space space left parenthesis straight x minus 12 right parenthesis space left parenthesis straight x minus 2 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space space space space space space straight x space equals space 12 space space space or space space straight x space equals space 2
       But, x cannot be less than 6.           
    So, x = 12.
    Hence, B alone can finish the work in 12 days.

    Question 202
    CBSEENMA10006790
    Wired Faculty App

    In a class, the sum of the marks obtained by P in Mathematics and Science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science, the product of marks obtained in the two subjects would have been 180. Find the marks obtained in the two subjects seperately. 

    Solution

    Let marks got by P in Mathematics = x
    Then, marks got by P in Science = (28 – x)
    Now, according to the given condition, we have
    (x + 3) (28 – x – 4) = 180
    ⇒ (x + 3) (24 – x) = 180
    ⇒ 24x – x2 + 72 – 3x = 180
    ⇒  –x2 + 21x + 72 – 180 = 0
    ⇒ –x2 + 21x – 108 = 0
    ⇒ x2 – 21x + 108 = 0
    ⇒  x2 – 12x – 9x + 108 = 0 ⇒ x(x – 12)– 9 (x – 12) = 0
    ⇒ (x – 12) (x – 9) = 0
    ⇒ x = 12
    or x = 9
    Hence if marks got by P in mathematics 12 then marks got by him in science = 28 – 12 =16 Ans.
    And if marks got by P in mathematics 9 then
    Marks got by him in science = 28 – 9 = 19 Ans.

    Question 203
    CBSEENMA10006791
    Wired Faculty App

    A trader bought a number of articles for Rs. 900. Five articles were found damaged. He sold each of the remaining articles at Rs. 2 more than what he paid for it. He got a profit of Rs. 80 on the whole transaction. Find the number of articles he bought.

    Solution

    No. of articles = x,
    Cost of each article = y
    According to question.
    Ist condition:  xy = 900,   straight y equals 900 over straight x
    2nd condition: left parenthesis straight x minus 5 right parenthesis space open parentheses 900 over straight x plus 2 close parentheses space equals space 900 plus 80
                      space space space space open parentheses straight x minus 5 close parentheses space open parentheses fraction numerator 900 plus 2 straight x over denominator straight x end fraction close parentheses space equals space 980
    fraction numerator 900 straight x plus 2 straight x squared minus 4500 minus 10 straight x over denominator straight x end fraction equals 980 

    2x2 + 890x – 4500 = 980x
    2x2 – 90x – 4500 = 0
    x2 – 45x – 2250 = 0
    x2 – 75x + 30x – 2250 = 0
    x(x –75) + 30(x – 75) = 0
    (x + 30) (x – 75) = 0
    x = – 30 (reject),
    x = 75
    No. of articles = 75.

    Question 204
    CBSEENMA10006792
    Wired Faculty App

    On a pillar 9 m high is perched a peacock. From a point 27 m away from the base of the pillar, a snake is coming to its hole at the bottom of the pillar. Seeing the snake, the peacock pounces on it. If their speeds are equal, at what distance from the hole is the snake caught?

    Solution
    Let the position of the peacock be ‘A’.
    Position of Hole is ‘B’. Let the position of the snake is ‘D’ and is coming towards the hole ‘B’. When snake is at position than peacock pounces on it.
    Let BC = x,
    then DC = (27– x)
    We have, AC = DC.
    Now, in right ΔABC
    AC2 = AB2 + BC2
    ⇒ (27 – x)2 = (9)2 + (x)2
    ⇒ 729 + x2 – 54x = 81+ x2
    ⇒ 54x = 779 – 81
    ⇒ 54x = 698
    ⇒ x = 12
    Hence, distance from the hole where the snake is caught = 12 cm.
     
    Question 255
    CBSEENMA10006860
    Wired Faculty App

    A motor boat whose speed is 18 km/h in still water takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. 

    Solution

    Let the speed of the stream be x km/hr.
    ∴ Speed of the boat upstream = (18 – x) km/hr.
    Speed of the boat downstream = (18 + x) km/hr.
    Time taken for going 24 km upstream = fraction numerator 24 over denominator 18 minus straight x end fraction space hours
    Time taken for going 24 km downstream = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    According to given condition,
    ∴        space fraction numerator 24 over denominator 18 minus straight x end fraction minus fraction numerator 24 over denominator 18 plus straight x end fraction equals 1
    rightwards double arrow space space 24 left parenthesis 18 plus straight x right parenthesis space minus space 24 left parenthesis 18 minus straight x right parenthesis space equals space left parenthesis 18 minus straight x right parenthesis left parenthesis 18 plus straight x right parenthesis rightwards double arrow space space space space space space space space space space space space space space straight x squared plus 48 straight x minus 324 space equals space 0
    Using the quadratic formula, we get
    straight x equals fraction numerator negative 48 plus-or-minus square root of 48 squared plus 1926 end root over denominator 2 end fraction equals fraction numerator negative 48 plus-or-minus square root of 3600 over denominator 2 end fraction equals space fraction numerator negative 48 plus-or-minus 60 over denominator 2 end fraction equals 6 space or space minus 54
    Since x is the speed of the stream, it cannot be negative. So, we ignore the root x = –54. Therfore, x = 6 gives the speed of the stream as 6km/h.
    rightwards double arrow space space space space space space space 21 over 4 cross times fraction numerator 2 straight x over denominator 25 minus straight x squared end fraction equals 1 rightwards double arrow space space space space space space space space space 21 over 2 cross times fraction numerator straight x over denominator 25 minus straight x squared end fraction equals 1 rightwards double arrow space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 21 straight x space equals space 50 minus 2 straight x squared
    rightwards double arrow space space space space space space space space space space space space space 2 straight x squared plus 21 straight x minus 50 space equals space 0 rightwards double arrow space space space space 2 straight x squared plus 25 straight x minus 4 straight x minus 50 space equals space 0 rightwards double arrow space space space space straight x left parenthesis 2 straight x plus 25 right parenthesis minus 2 left parenthesis 2 straight x plus 25 right parenthesis space equals space 0 rightwards double arrow space space space space space space space space space space space space space left parenthesis 2 straight x plus 25 right parenthesis space left parenthesis straight x minus 2 right parenthesis space equals space 0 rightwards double arrow space space 2 straight x space plus 25 space equals 0 space space space space space space straight x space minus space 2 space equals 0 rightwards double arrow space space space space space 2 straight x space equals space minus 25 space space space space space rightwards double arrow space space straight x space equals space 2 rightwards double arrow space space space space space straight x space equals space fraction numerator negative 25 over denominator 2 end fraction
    straight x equals fraction numerator negative 25 over denominator 2 end fraction  is rejected.
    Hence, the speed of the stream is 2 km/hr.

    Question 259
    CBSEENMA10006866
    Wired Faculty App

    Solve for 'x':   fraction numerator 1 over denominator left parenthesis straight x minus 1 right parenthesis space left parenthesis straight x minus 2 right parenthesis end fraction plus fraction numerator 1 over denominator left parenthesis straight x minus 2 right parenthesis left parenthesis straight x minus 3 right parenthesis end fraction plus fraction numerator 1 over denominator left parenthesis straight x minus 3 right parenthesis left parenthesis straight x minus 4 right parenthesis end fraction equals 1 over 6
    Solution

    Solution not provided.
    Ans. x = 7  or x = -2

    Question 260
    CBSEENMA10006869
    Wired Faculty App

    For what value of p (4 – p)x2 – (2p + 4)x + (8p + 1) = 0 is a perfect square.

    Solution

    Solution not provided.
    Ans. p = 0, 3

    Question 262
    CBSEENMA10006871
    Wired Faculty App

    Find the value of ‘K’ for which the equation Kx2 + Kx + 1 = –4x2 – x has real and equal roots.

    Solution

    Solution not provided.
    Ans. K = 5, -3

    Question 263
    CBSEENMA10006872
    Wired Faculty App

    The sum ‘S’ of first n natural numbers is given by the relation
    space straight S equals fraction numerator straight n left parenthesis straight n plus 1 right parenthesis over denominator 2 end fraction
    Find n, if the sum is 276.

    Solution

    Solution not provided.
    Ans.  n = 23

    Question 267
    CBSEENMA10006876
    Wired Faculty App

    Find the roots of the following equation:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans. open curly brackets negative 3 comma space minus 2 comma space fraction numerator negative 1 over denominator 2 end fraction comma space 3 close curly brackets

    Question 268
    CBSEENMA10006877
    Wired Faculty App

    Find the roots of the following equation:
    open parentheses fraction numerator 2 straight x minus 1 over denominator straight x minus 1 end fraction close parentheses to the power of 4 minus 10 open parentheses fraction numerator 2 straight x plus 1 over denominator straight x minus 1 end fraction close parentheses squared plus 9 equals 0

    Solution

    Solution not provided.
    Ans. open curly brackets negative 2 comma space 0 comma space 4 comma space 2 over 5 close curly brackets

    Question 270
    CBSEENMA10006880
    Wired Faculty App

    The perimeter of a rectangular plot is 42 metres and its area is 108 m2 Find the dimensions of the plot.

    Solution

    Solution not provided.
    Ans. length = 12 m,  breadth = 9 m

    Question 273
    CBSEENMA10006891
    Wired Faculty App

    Solve for 'x': space space fraction numerator 1 over denominator straight x plus 1 end fraction plus fraction numerator 2 over denominator straight x plus 2 end fraction equals fraction numerator 4 over denominator straight x plus 4 end fraction comma space space straight x not equal to 1 comma space minus 2 comma space minus 4
    Solution

    Solution not provided.
    Ans. 2 plus-or-minus 2 square root of 3

    Question 274
    CBSEENMA10006893
    Wired Faculty App

    Solve the following equation by using quadratic formula:
    10x2 + 3bx + a2 – 7ax – b2 = 0.

    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 278
    CBSEENMA10006897
    Wired Faculty App

    Find the discriminant of the quadratic equation 9x2 – 12x + 4 = 0, hence find the nature of its roots.

    Solution

    Solution not provided.
    Ans. equal and real roots.

    Question 279
    CBSEENMA10006898
    Wired Faculty App

    For what value of k, does the quadratic equation 9x2 + 8kx + 16 = 0 has equal roots?

    Solution

    Solution not provided.
    Ans. space space straight k equals plus-or-minus 3

    Question 285
    CBSEENMA10006908
    Wired Faculty App

    Determine value(s) of p for which the quadratic equation 4x2 – 3px + 9 = 0 has real roots.

    Solution

    Solution not provided.
    Ans.  straight p less or equal than negative 4 

    Question 288
    CBSEENMA10006911
    Wired Faculty App

    Determine value(s) of p for which the quadratic equation 2x2 + 3x + p = 0 has real roots.

    Solution

    Solution not provided.
    Ans.    straight p less or equal than 1 over 8

    Question 291
    CBSEENMA10006915
    Wired Faculty App

    Find the quadratic polynomial whose sum and product of its zeroes are <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> respectively.

    Solution

    Solution not provided.
    Ans.   3 straight x squared minus 3 square root of 2 straight x plus 1

    Question 292
    CBSEENMA10006916
    Wired Faculty App

    Solve for x: <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> given that straight x not equal to negative 3 comma space straight x not equal to 1 half
    Solution

    Solution not provided.
    Ans.   -10, <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 293
    CBSEENMA10006918
    Wired Faculty App

    Solve for x: space 2 open parentheses fraction numerator straight x minus 1 over denominator straight x plus 3 end fraction close parentheses minus 7 open parentheses fraction numerator straight x plus 3 over denominator straight x minus 1 end fraction close parentheses equals 5 semicolon given that straight x not equal to 3 comma space straight x not equal to 1
    Solution

    Solution not provided.
    Ans.   negative 1 comma space fraction numerator negative 23 over denominator 5 end fraction

    Question 294
    CBSEENMA10006919
    Wired Faculty App

    Solve for x: <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Solution

    Solution not provided.
    Ans.   space space straight x equals fraction numerator 2 straight a plus straight b over denominator 3 end fraction comma space straight y space equals space fraction numerator straight a plus 2 straight b over denominator 3 end fraction

    Question 295
    CBSEENMA10006921
    Wired Faculty App

    Solve for x: <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> given that straight x not equal to 3 comma space space straight x not equal to fraction numerator negative 3 over denominator 2 end fraction
    Solution

    Solution not provided.
    Ans.   x = 6,  x = 1

    Question 297
    CBSEENMA10006923
    Wired Faculty App

    Solve for <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Solution

    Solution not provided.
    Ans.   <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 299
    CBSEENMA10006925
    Wired Faculty App

    Solve for <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Solution

    Solution not provided.
    Ans.   x = -a, x = -b

    Question 300
    CBSEENMA10006926
    Wired Faculty App

    The sum of two numbers is 16 and the sum of their reciprocals is space 1 third. Find the numbers.

    Solution

    Solution not provided.
    Ans.   12 and 4 or 4 and 12

    Question 301
    CBSEENMA10006927
    Wired Faculty App

    The sum of two numbers is 18. The sum of their reciprocals is 1 fourth. Find the numbers.

    Solution

    Solution not provided.
    Ans.   6, 12 or 12, 6

    Question 302
    CBSEENMA10006929
    Wired Faculty App

    Solve for x: a2 b2 x2 + b2 x – a2 x – 1 = 0

    Solution

    Solution not provided.
    Ans.   negative fraction numerator negative 1 over denominator straight a squared end fraction or space 1 over straight b squared

    Question 304
    CBSEENMA10006931
    Wired Faculty App

    Using quadratic formula, solve for x: 9x2 – 3(a + b)x + ab = 0

    Solution

    Solution not provided.
    Ans.   space straight a over 3 comma space straight b over 3.

    Question 305
    CBSEENMA10006933
    Wired Faculty App

    Solve for x: 12abx2 – (9a2 – 8b2)x – 6ab = 0

    Solution

    Solution not provided.
    Ans.   fraction numerator 3 straight a over denominator 4 straight b end fraction space or space fraction numerator negative 2 straight b over denominator 3 straight a end fraction

    Question 307
    CBSEENMA10006935
    Wired Faculty App

    Using the quadratic formula, solve the equation: a2b2x2 – (4b4 – 3a4) x – 12a2b2 = 0.

    Solution

    Solution not provided.
    Ans.   space space space fraction numerator 4 straight b squared over denominator straight a squared end fraction comma space fraction numerator negative 3 straight a squared over denominator straight b squared end fraction

    Question 310
    CBSEENMA10006939
    Wired Faculty App

    The difference of two numbers is 5 and the difference of their reciprocals is 1 over 10. Find the numbers.

    Solution

    Solution not provided.
    Ans.  -5, -10 or 10, 5

    Question 316
    CBSEENMA10006948
    Wired Faculty App

    Find the roots of the following equations.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans.  1,  2

    Question 321
    CBSEENMA10006953
    Wired Faculty App

    The sum of the squares of two consecutive odd numbers is 394. Find the numbers.

    Solution

    Solution not provided.
    Ans. 13, 15 or -15, +3

    Question 322
    CBSEENMA10006954
    Wired Faculty App

    Solve the following equation for x: 9x2 – (a + b)x + (2a2 + 5ab + 2b2) = 0.

    Solution

    Solution not provided.
    Ans. straight x equals fraction numerator 2 straight a plus straight b over denominator 3 end fraction comma space straight x equals fraction numerator straight a plus 2 straight b over denominator 3 end fraction

    Question 323
    CBSEENMA10006955
    Wired Faculty App

    Solve the following equation for x: 9x2 – (a + b)x + (2a2 + 5ab + 2b2) = 0.

    Solution

    Solution not provided.
    Ans. straight x equals fraction numerator 2 straight a plus straight b over denominator 3 end fraction comma space straight x equals fraction numerator straight a plus 2 straight b over denominator 3 end fraction

    Question 325
    CBSEENMA10006958
    Wired Faculty App

    Write the values of k for which the quadratic equation : x2 – kx + 9 = 0 has equal roots.

    Solution

    Solution not provided.
    Ans.   straight k equals plus-or-minus 6

    Question 329
    CBSEENMA10006962
    Wired Faculty App

    Write the nature of the roots of quadratic equation 4 straight x squared plus 4 square root of 3 straight x plus 3 equals 0

    Solution

    Solution not provided.
    Ans.   Real and equal.

    Question 333
    CBSEENMA10006968
    Wired Faculty App

    Discriminant of x2 + 5x + 5 = 0 is
    • 5 over 2
    • –5 
    • 5

    • -4
    Solution

    C.

    5
    Question 336
    CBSEENMA10007037
    Wired Faculty App

    The solutions of 2x2 – 5x + 3 = 0 are
    • 3 over 2 comma space minus 1
    • negative 3 over 2 comma space minus 1
    • <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    • space 1 half comma space 3 over 2

    Solution

    C.

    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 337
    CBSEENMA10007038
    Wired Faculty App

    The sum of roots of a quadratic equation x2 + 4x – 320 = 0 is:

    • -4

    • 4
    • 1 fourth
    • 1 half

    Solution

    A.

    -4

    Question 338
    CBSEENMA10007039
    Wired Faculty App

    The product of roots of a quadratic equation 2x2 – 7x – 4 = 0 is:
    • 2 over 7
    • fraction numerator negative 2 over denominator 7 end fraction
    • fraction numerator negative 4 over denominator 7 end fraction
    • <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    D.

    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 345
    CBSEENMA10007046
    Wired Faculty App

    One of the root of a quadratic equation space square root of 2 straight x squared plus 7 straight x plus 5 square root of 2 space equals space 0
    • space fraction numerator negative 5 over denominator square root of 2 end fraction
    • <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    B.

    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 346
    CBSEENMA10007047
    Wired Faculty App

    The discriminant of the quadratic equation 3 straight x squared minus 4 square root of 3 straight x plus 4 equals 0
    • D > 0 
    • D < 0
    • D = 0
    • D = 40

    Solution

    C.

    D = 0
    Question 347
    CBSEENMA10009587
    Wired Faculty App

    If -5 is a root of the quadratic equation 2x2  + px – 15 = 0 and the quadratic equation p(x2 + x)k = 0 has equal roots, find the value of k.
    Solution

    We Given -5 is a root of the quadratic equation 2x2+px-15 =0
    , -5 satisfies the given equation.
    ∴ 2 (-5)2 +p(-5)-15=0
    50-5p-15 =0
    35-5p=0
    5p=35 ⇒ p=7
    Substituting p=7 in (x2+x)+k =0, we get
    7(x2+x)+k =0
    7x2+7x+k=0
    The roots of the equation are equal
    ∴ Discriminant =b2-4ac =0
    Here, a= 7, b=7,c=k
    b2-4ac=0
    ∴(7)2-4(7)(k) =0
    49-28k =0
    28k=49
    k= 49/28 
    =7/4

    Question 348
    CBSEENMA10009598
    Wired Faculty App

    Solve for x:
    fraction numerator 1 over denominator left parenthesis straight x minus 1 right parenthesis left parenthesis straight x minus 2 right parenthesis end fraction plus fraction numerator 1 over denominator left parenthesis straight x minus 2 right parenthesis left parenthesis straight x minus 3 right parenthesis end fraction space equals 2 over 3 comma space straight x not equal to 1 comma 2 comma 3
    Solution
    fraction numerator 1 over denominator left parenthesis straight x minus 1 right parenthesis left parenthesis straight x minus 2 right parenthesis end fraction plus fraction numerator 1 over denominator left parenthesis x minus 2 right parenthesis left parenthesis x minus 3 right parenthesis end fraction equals 2 over 3 therefore fraction numerator left parenthesis straight x minus 3 right parenthesis plus left parenthesis straight x minus 1 right parenthesis over denominator left parenthesis straight x minus 1 right parenthesis left parenthesis straight x minus 2 right parenthesis left parenthesis straight x minus 3 right parenthesis end fraction space equals 2 over 3 therefore fraction numerator straight x minus 3 plus straight x minus 1 over denominator left parenthesis straight x squared minus 2 straight x minus straight x plus 2 right parenthesis left parenthesis straight x minus 3 right parenthesis end fraction space equals 2 over 3 therefore fraction numerator 2 straight x minus 4 over denominator left parenthesis straight x squared minus 3 straight x plus 2 right parenthesis left parenthesis straight x minus 3 right parenthesis end fraction space equals space 2 over 3 therefore fraction numerator 2 straight x minus 4 over denominator straight x cubed minus 3 straight x squared minus 3 straight x squared plus 9 straight x plus 2 straight x minus 6 end fraction space equals 2 over 3 therefore space fraction numerator 2 straight x minus 4 over denominator straight x cubed minus 6 straight x squared plus 11 straight x minus 6 end fraction space equals 2 over 3 therefore 6 straight x minus 12 equals 12 straight x cubed minus 12 straight x squared plus 22 space straight x minus 12 therefore 2 straight x cubed minus 12 straight x squared plus 16 straight x equals 0 therefore 2 straight x left parenthesis straight x squared minus 6 straight x plus 8 right parenthesis space equals 0 therefore left parenthesis straight x squared minus 6 straight x plus 8 right parenthesis space equals 0 straight x squared minus 4 straight x minus 2 straight x plus 8 space equals 0 straight x left parenthesis straight x minus 4 right parenthesis minus 2 left parenthesis straight x minus 4 right parenthesis equals 0 therefore space left parenthesis straight x minus 4 right parenthesis left parenthesis straight x minus 2 right parenthesis space equals 0 straight x equals 4 space or space straight x equals 2
    Question 349
    CBSEENMA10009607
    Wired Faculty App

    Solve for x:

    fraction numerator 1 over denominator straight x plus 1 end fraction plus fraction numerator 2 over denominator x plus 2 end fraction plus fraction numerator 4 over denominator x plus 4 end fraction comma space x not equal to negative 1 comma negative 2 comma negative 4
    Solution
    fraction numerator 1 over denominator straight x plus 1 end fraction plus fraction numerator 2 over denominator straight x plus 2 end fraction plus fraction numerator 4 over denominator straight x plus 4 end fraction straight L. straight C. straight M space of space all space the space denominators space is space left parenthesis straight x plus 1 right parenthesis left parenthesis straight x plus 2 right parenthesis left parenthesis straight x plus 4 right parenthesis Multiply space throughtoout space by space the space straight L. straight C. straight M space we space get left parenthesis straight x plus 2 right parenthesis left parenthesis straight x plus 4 right parenthesis plus 2 left parenthesis straight x plus 1 right parenthesis left parenthesis straight x plus 4 right parenthesis space equals 4 left parenthesis straight x plus 1 right parenthesis left parenthesis straight x plus 2 right parenthesis therefore left parenthesis straight x plus 4 right parenthesis left parenthesis straight x plus 2 plus 2 straight x plus 2 right parenthesis equals 4 left parenthesis straight x squared plus 3 straight x plus 2 right parenthesis therefore space left parenthesis straight x plus 4 right parenthesis left parenthesis 3 straight x plus 4 right parenthesis space equals 4 straight x squared plus 12 straight x space plus 8 therefore space 3 straight x squared plus 16 straight x plus 16 space equals space 4 straight x squared plus 12 straight x plus 8 therefore space straight x squared minus 4 straight x minus 8 equals 0 Now space straight a comma space equals 1 space straight b equals negative 4 comma space straight c equals negative 8 straight x equals fraction numerator negative straight b begin display style plus for minus of end style square root of straight b squared minus 4 ac end root over denominator 2 straight a end fraction equals fraction numerator 4 plus for minus of square root of 16 plus 32 end root over denominator 2 end fraction space equals fraction numerator 4 plus for minus of square root of 48 over denominator 2 end fraction space equals fraction numerator 4 plus for minus of 4 square root of 3 over denominator 2 end fraction space straight x equals 2 plus for minus of 2 square root of 3
    Question 350
    CBSEENMA10009614
    Wired Faculty App

    If the quadratic equation has px squared minus 2 square root of 5px plus 15 equals 0 two roots, then find the value of p.
    Solution

    The given quadratic equation has px squared minus 2 square root of 5px plus 15 equals 0 two equal roots.
    therefore,
    by using the discriminant method
    straight b squared space minus space 4 ac space equals space 0 space.. left parenthesis straight i right parenthesis straight b space equals space minus 2 square root of 5 straight p straight a space space equals space straight p straight c space equals space 15 thus comma space putting space the space value space in space equation space left parenthesis straight i right parenthesis left parenthesis negative 2 square root of 5 straight p end root right parenthesis squared minus 4 space straight x space straight p space straight x 15 space equals 0 rightwards double arrow space left parenthesis negative 2 square root of 5 straight p right parenthesis squared minus 4 space straight x space straight p space straight x 15 space equals 0

    ⇒  20p2 - 60p = 0
    ⇒  20p (p - 3) = 0
    ⇒  p = 0 or p - 3 = 0
    ⇒  p = 0 or p = 3
    p cannot be zero.
    Hence, the value of p  is 3. 

    Question 351
    CBSEENMA10009620
    Wired Faculty App

    Solve the following quadratic equation for x,

    4x2 + 4bx - (a2 - b2) = 0
    Solution

    Given equation,
    4x2 + 4bx - (a2 - b2) = 0 
    ⇒ 4x2  +4bx - ( a + b) (a - b) = 0
    ⇒ 4x2 + 2[(a + b) - (a - b)] x - (a + b)(a-b) = 0
    ⇒ 4x2 +2 (a + b)x - 2(a - b)x - (a + b ) (a - b) = 0
    ⇒ 2x [2x + (a + b)] [(a - b)[2x + (a + b)] = 0
    ⇒ 2x + (a + b) = 0 or 2x - (a - b) = 0
    ⇒ x =  - (a + b)/2 OR x = (a - b)/2

    Question 352
    CBSEENMA10009625
    Wired Faculty App

    solve for x:

    square root of 3 straight x squared space minus 2 square root of 2 straight x space minus 2 square root of 3 space equals space 0
    Solution
    Given comma square root of 3 straight x squared space minus space 2 square root of 2 straight x space minus space 2 square root of 3 space equals space 0 rightwards double arrow space space square root of 3 straight x squared space minus space 3 square root of 2 straight x space plus square root of 2 straight x minus space 2 square root of 3 space equals space 0 rightwards double arrow space space square root of 3 straight x space left parenthesis straight x space minus square root of 6 right parenthesis space plus square root of 2 space left parenthesis straight x space minus space square root of 6 right parenthesis space equals space 0 rightwards double arrow space space left parenthesis straight x space minus space square root of 6 right parenthesis space equals 0 space or space square root of 3 straight x space plus space square root of 2 space equals space 0 rightwards double arrow space straight x space equals space square root of 6 space or space straight x space equals space minus square root of 2 over 3 end root Thus space value space of space straight x space equals space square root of 6 space and space space minus square root of 2 over 3 end root
    Question 353
    CBSEENMA10009648
    Wired Faculty App

    Find the roots of the quadratic equation  square root of 2 straight x squared space plus 7 straight x space plus 5 square root of 2 space equals space 0
    Solution
    square root of 2 straight x squared space plus 7 straight x space plus 5 square root of 2 space equals space 0 or rightwards double arrow square root of 2 straight x squared space plus 5 straight x space plus 2 straight x space plus 5 square root of 2 space equals space 0 rightwards double arrow straight x left parenthesis square root of 2 straight x space plus 5 right parenthesis space plus square root of 2 left parenthesis square root of 2 straight x end root plus 5 right parenthesis space equals space 0 rightwards double arrow space left parenthesis square root of 2 straight x end root space plus 5 right parenthesis left parenthesis straight x plus square root of 2 right parenthesis space equals space 0 rightwards double arrow left parenthesis square root of 2 straight x end root space plus 5 right parenthesis space left parenthesis straight x plus square root of 2 right parenthesis space equals space 0 rightwards double arrow space straight x space plus space square root of 2 space equals space 0 square root of 2 straight x end root space plus 5 space equals space 0 rightwards double arrow space straight x space equals negative square root of 2 straight x space equals negative space fraction numerator 5 over denominator square root of 2 end fraction space equals negative space fraction numerator 5 square root of 2 over denominator 2 end fraction space Hence space roots space are space minus square root of 2 comma space minus fraction numerator 5 square root of 2 over denominator 2 end fraction space
    Question 354
    CBSEENMA10009651
    Wired Faculty App

    Find the value of k for which the equation x2 + k(2x + k − 1) + 2 = 0 has real and equal roots. 
    Solution

    The given equation is x2+k(2x+k−1)+2=0.
    ⇒x2+2kx+k(k−1)+2=0
    So, a = 1, b = 2k, c = k(k − 1) + 2
    We know D=b2−4ac
    ⇒D=(2k)2−4×1×[k(k−1)+2]
    ⇒D=4k2−4[k2−k+2]
    ⇒D=4k2−4k2+4k−8
    ⇒D=4k−8=4(k−2)
    For equal roots, D = 0
    Thus, 4(k − 2) = 0
    So, k = 2.

    Question 355
    CBSEENMA10009657
    Wired Faculty App

    If the equation (1 + m2) x2 + 2mcx + c2 – a2 = 0 has equal roots then show that c2 = a2 (1 + m2). 
    Solution

    Given quadratic equation: (1 + m2)x2 + 2mcx + (c2 – a2) = 0
    The given equation has equal roots, therefore
    D = b2 − 4ac = 0 ..... (1)
    From the above equation, we have
    a = (1 + m2)
    b = 2mc
    and c = (c2 – a2)
    Putting the values of a, b and c in (1), we get
    D = (2mc)2 − 4(1 + m2) (c2 – a2) = 0
    ⇒ 4m2c2 − 4 (c2 + c2m2 − a2 − a2m2) = 0
    ⇒ 4m2c2 − 4c2 − 4c2m2 + 4a2 + 4a2m2 = 0
    ⇒ −4c2 + 4a2 + 4a2m2 = 0
    ⇒ 4c2 = 4a2 + 4a2m2
    ⇒ c2 = a2 + a2m2
    ⇒ c2 = a2(1 + m2)
    Hence, proved.

    Question 356
    CBSEENMA10009668
    Wired Faculty App

    Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream. 
    Solution

    Let the speed of the stream be x km/h.
    It is given that the speed of a boat in still water is 15 km/h.
    Now,
    Speed of the boat upstream = Speed of the boat in still water − Speed of the stream = (15 − x) km/h
    Speed of the boat downstream = Speed of the boat in still water + Speed of the stream = (15 + x) km/h
    We know that
    Time=Distance/Speed
    Time is taken for upstream journey + Time taken for the downstream journey = 4 h 30 min
    therefore space fraction numerator 30 over denominator 15 minus straight x end fraction space plus fraction numerator 30 over denominator 15 plus straight x end fraction space equals space 4 1 half rightwards double arrow space 30 open square brackets fraction numerator open parentheses 15 plus straight x close parentheses plus open parentheses 15 minus straight x close parentheses over denominator open parentheses 15 plus straight x close parentheses open parentheses 15 minus straight x close parentheses end fraction close square brackets space equals space 9 over 2 rightwards double arrow space 30 space open parentheses fraction numerator 30 over denominator 225 minus straight x squared end fraction close parentheses space equals space 9 over 2 rightwards double arrow space 225 minus straight x squared space equals space fraction numerator 30 space straight x 30 space straight x 2 over denominator 9 end fraction rightwards double arrow space 225 minus straight x squared space equals space 200 rightwards double arrow space straight x squared space equals space 225 minus 200 space equals space 25 rightwards double arrow space straight x space equals space plus-or-minus 5

    Since speed can not be negative, therefore, x = 5.
    Thus, the speed of the stream is 5 km/h.

    Question 357
    CBSEENMA10009682
    Wired Faculty App

    If x = 3 is one root of the quadratic equation x2-2kx -6 =0, the find the value of k.
    Solution

    x = 3 is one of the root of x2-2kx -6 =0

    (3)2 -2k(3) - 6 =0

    9-6k - 6 = 0
    3 - 6k = 0
    3 = 6k
    k = 3/6 = 1/2

    Question 358
    CBSEENMA10009696
    Wired Faculty App

    A plane left 30 minutes late than its scheduled time and in order to reach the destination 1500 km away in time, it had to increase its speed by 100 km/h from the usual speed. Find its usual speed.
    Solution

    Let the usual speed of the plane be x km/hr

    Time taken to cover 1500 km with usual speed, t1 = 1500xhr

    Time taken to cover 1500 km with speed of (x +100) km/hr, t2= 1500x + 100 hrs

    Difference between t1 - t2 =30 min = 1/2

    ∴ 1500x = 1500x + 100 + 121500x -1500x  + 100 = 121500x + 100 - xx(x + 100) = 12150000 x 2 = x(x + 100)x2 + 100 x -300000 = 0solving equation,x = -600 or x = 500

    But speed can't be negative
    Hence, usual speed 500 km/hr.

    Question 359
    CBSEENMA10009708
    Wired Faculty App

    A motor boat whose speed is 18 km/hr in still water 1 hr more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
    Solution

    Let the speed of stream be x km/hr

    Now, for upstream,speed = (18-x) km/hr

    ∴ time taken = 2418 -xhr

    Now, for downstream;speed = (18 +x) km/hr

    ∴ time taken = 2418 +xhr

    Given that, 

    2418-x =2418 + x +1-1 = 2418 +x - 2418-x-1 = 24 [ (18-x) - (18 +x)(18)2 -x2- 1 = 24 [-2x]324 -x2-324 + x2 = - 48 xx2 + 48 x -324 = 0x2 + 54x -6x - 324 = 0(x +54)(x-6) =0x = - 54 or x = 6x = -54 km/hr x = 6

    Speed can never be negative, -54 km/hr

    hence speed of the stream 6 km/hr

    Question 360
    CBSEENMA10009709
    Wired Faculty App

    A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr more than its original speed.  It takes 3 hours to complete the total journey, what is the original average speed ?
    Solution

    Let x be the original average speed of the train for 63 km.

    Then, (x + 6) will be the new average speed for the remaining 72 km.

    Total time taken to complete the journey is 3 hrs.

    ∴ 63x + 72(x + 6) = 3∵ Time =Distancespeed∴ 63x +378 + 72xx (x+ 6) = 3⇒ 135 x + 378 = 3x2 + 18x⇒ x2 - 39x -126 = 0⇒ (x-42)(x+3) = 0⇒ x = 42or x  = -3

    Since speed can not be negative.
    Therefore x = 42 km/hr.

    Question 361
    CBSEENMA10009720
    Wired Faculty App

    Solve the following quadratic equation for x;43x2 + 5x - 23 = 0 
    Solution

    43 x2 + 5x -23 = 0⇒ 43 x2  + 8x - 3x - 23 = 0⇒4x ( 3 x + 2 ) - 3 (3 x + 2) = 0⇒(4x - 3) (3x + 2 ) = 0∴ x = 34   or  x = -23

    Question 362
    CBSEENMA10009724
    Wired Faculty App

    For what values of k, the roots of the quadratic equation
    (k + 4) x2 + (k + 1)x + 1 = 0 are equal?
    Solution

       ( k+4) x2 + (k + 1 ) x +1 = 0a = k +4,  b = k + 1,  c= 1For equal roots, discriminant,  D = 0⇒b2- 4ac = 0⇒( k + 1 )2 - 4( k + 4 ) x 1=0⇒k2+ 2k +1 -4k -16 = 0⇒k2 - 2k - 15 = 0⇒k2 -5k + 3k - 15 = 0⇒k( k - 5 ) + 3 ( k - 5 ) = 0⇒( k - 5 ) ( k + 3 ) = 0⇒k = 5 or k = -3Thus, for k = 5 or  k = -3, the given quadratic equation has equal roots.

    Question 363
    CBSEENMA10009730
    Wired Faculty App

    Solve that following for x:            12a+b+2x = 12a + 1b + 12x

     
    Solution

    12a+b+2x = 12a +1b +12x⇒12a+b+2x - 12x =  12a +1b⇒2x-2a-b-2x2x(2a+b+2x) =b+2a2ab⇒-2a-b2x(2a+b+2x)  = b+2a2ab⇒-1x(2a+b+2x) =1ab  ⇒2x2 +2ax+bx+ab=0⇒2x(x+a)+b(x+a)=0⇒(2x+b) (x+a)=0⇒2x+b=0  or  x+a=0⇒2x=-b  or  x= -a⇒x=-b2 or   x= -a

    Question 364
    CBSEENMA10009758
    Wired Faculty App

    Find the values of k for which the quadratic equation

    9x2 - 3kx + k = 0 has equal roots.
    Solution

    Given Quadratic equation  9x2 - 3kx + k = 0 has equal roots.

    Let β be the equal roots of the equationThus 2β = 3k9 = k3      ( Sum of the roots is equal to  -ba )We get β = k6And we also know that  β2 = k9    (Product of the roots is equal to ca )     k236  = k9For K≠ 0,  k36 = 19Thus K= 4

    Question 365
    CBSEENMA10009763
    Wired Faculty App

    Solve for x:
       

    16x - 1 = 15x+1;     x ≠ 0, -1
    Solution

    16x -1 = 15x+116-xx = 15x+115x = 16x + 16 - x2 - x16 = x2x = 4

    Question 366
    CBSEENMA10009771
    Wired Faculty App

    A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
    Solution

    let speed of stream = x km/h

    Speed of boat in steel water = 18 km/h

    speed of boat in upstream = (18 - x )  km/h

    speed of boat in downstream = (18 + x )  km/h

    Distance = 24 km

    As per question, 

    24km18-x = 24km18+x + 1x2 + 48x - 324 = 0x2  + 54x - 6x -324 = 0x( x + 54 ) - 6 ( x+ 54) =0x-6 = 0 or  x+ 54 = 0x = 6  or  -54Hence, the speed of stream = 6 km/h

     

    Question 367
    CBSEENMA10009773
    Wired Faculty App

    Solve for x:

      x-3x-4 + x-5x-6 = 103;      x ≠ 4, 6
    Solution

    x-3x-4 + x-5x-6 = 103x-3 x-6 +x-4 x-5x-4 x-6 = 1032x2 - 9x + 19x2 - 10x + 24 = 1032x2 - 23x + 63 = 0 x= 7 or    x = 92

    Question 368
    CBSEENMA10009787
    Wired Faculty App

    Find the value of p, for which one root of the quadratic equation px2 – 14x + 8= 0 is 6 times the other.
    Solution

    Given, px2 -14x +8 =0Here, a = p,  b =  -14,  c = 8Let α and β be the roots of the given quadratic equation.Then,  β = 6αNow, sum of the roors = -ba⇒α + β = -(-14)p⇒α + β = 14p⇒α + 6 α = 14p⇒ 7α = 14p⇒ α = 2p  ...........(i)Product of the roots = ca⇒ αβ = 8p⇒α x 6α = 8p⇒ 6α2 = 8p ⇒ 3α2 = 4p⇒3 x 2p2= 4p  ............From (i)⇒3 x 4p2 = 4p⇒p = 3

    Question 369
    CBSEENMA10009797
    Wired Faculty App

    If the roots of the equation (a2 + b2) x2 + 2(ac + bd) x + (c2 + d2 ) = 0 are
    equal, prove that   ab = cd.
    Solution

    We have,

    (a2 + b2) x2 + 2(ac + bd) x + (c2 + d2 ) = 0 

    The discriminant of the given equation is given by

    ⇒ D = -2 ac + bd2 - 4 x a2 + b2 x c2 + d2⇒ D = 4 (ac + bd)2 - 4 x a2c2+ a2d2 + b2c2 + b2d2  ⇒ D = 4 a2c2 +  b2d2 + 2abcd - 4 x a2c2+ a2d2 + b2c2 + b2d2⇒ D =  4 x (a2c2 +  b2d2 + 2abcd  - a2c2- a2d2 - b2c2 - b2d2)⇒ D = 4 x ( 2abcd - a2d2 - b2c2 )⇒ D = -4 x    ( ad) 2 +  bc 2 - 2 ( ad )  (bc )⇒ D= -4 ( ad - bc )2The given equation will have equal roots, if  D = 0⇒ -4 ( ad - bc )2 = 0⇒   ( ad - bc )2  = 0⇒    ad - bc = 0⇒    ad = bc⇒  ab = cd

    Question 370
    CBSEENMA10009805
    Wired Faculty App

    Solve for x:

    x - 12x + 1 + 2x + 1x - 1 = 2,    Where x≠ -12, 1
    Solution

    x - 12x + 1 + 2x + 1x - 1 = 2(x - 1)2 + ( 2x + 1 )2( 2x + 1) ( x - 1) = 2⇒ x2 - 2x + 1 + 4x2 + 4x + 12x2 - 2x + x -1 = 2⇒ 5x2 + 2x + 22x2 - x - 1 = 2⇒ 5x2 + 2x + 2 = 4x2 -2x - 2⇒ 5x2 + 2x + 2 - 4x2 +2x + 2 = 0⇒ x2+ 4x + 4  = 0⇒ x2+ 2x + 2x + 4  = 0⇒ x(x + 2) + 2(x + 2) = 0⇒ ( x + 2) ( x + 2) = 0⇒ ( x + 2)2 = 0⇒ x + 2 = 0⇒ x = -2

    Question 371
    CBSEENMA10009806
    Wired Faculty App

    A takes 6 days less than B to do a work. If both A and B working together can do it in 4 days, how many days will B take to finish it?
    Solution

    Suppose B alone takes x days to to finish the work.

    Then, A alone can finish it in (x-6) days.

    (A's one days work) + (B's one day work) = 1x - 6 + 1x

    And, ( A+B)'s one day's work = 14

    ∴1x - 6 + 1x = 14⇒x + x - 6x(x - 6) = 14⇒2x - 6x2 - 6x = 14⇒8x - 24 = x2 - 6x⇒x2 - 6x - 8x + 24 = 0⇒x2 - 14x + 24 = 0⇒x2 - 12x - 2x + 24 = 0⇒ x(x - 12) -2(x - 12) = 0⇒(x-12) (x-2) = 0⇒x - 12 = 0  or  x - 2 = 0⇒ x = 12   or   x = 2

    But, x cannot be less than 6.

    So,  x = 12

    Hence, B alone can finish the work in 12 days.

    Question 372
    CBSEENMA10009814
    Wired Faculty App

    If 1 is a root of the equations ay2 + ay + 3 = 0 and y2 + y + b = 0, then ab equals

    • 3

    • -72

    • 6

    • -3
    Solution

    A.

    3

    It is given that 1 is the root of the equations 

    ay2 + ay + 3 = 0     and    y2 + y + b = 0.

    Therefore, y = 1 will satisfy both the equations.

     

    ∴ a(1)2 + a(1) + 3 = 0⇒ a + a + 3 = 0⇒2a + 3 = 0⇒a = -32Also, (1)2 + (1) + b = 0⇒ 1 + 1 + b = 0⇒ b = -2∴  ab = -32 x  -2 = 3

     

    Question 373
    CBSEENMA10009824
    Wired Faculty App

    Find the values (s) of k so that the quadratic equation  3x2 - 2kx + 12 = 0 has equal roots.
    Solution

    Given quadratic equation is  3x2 - 2kx + 12 = 0

    Here  a = 3,  b = -2k,   c = 12

    The quadratic equation will have equal roots if ∆ = 0.

     ∴  b2 - 4ac = 0

    Putting the values of  a, b  and  c  we get 

     

    = ( -2k )2 - 4 (3) (12) = 0

    ⇒ 4k 2 - 144 = 0

    ⇒  4k 2 = 144 

    ⇒ k2 = 1444⇒ k = 36 Considering square root on both sides,     k = 36 = ± 6

    Therefore, the required values of k are  6  and  -6.

    Question 374
    CBSEENMA10009830
    Wired Faculty App

    Solve for x:  4x2 – 4ax + (a2 – b2) = 0


                                       OR


    Solve for x:  3x2 - 6x + 2 = 0
    Solution

    = 4x2 - 4ax + ( a2 - b2 ) = 0⇒  4x2 - 4ax +  a2  - b2 = 0⇒ (2x)2 - 2 x 2ax + a2 - b2 = 0⇒ (2x - a)2 - b2 = 0⇒ (2x - a ) - b (2x - a ) + b = 0⇒ (2x - a ) - b = 0         or     (2x - a ) + b = 0 ⇒ 2x = a+b       or       2x = a - b⇒ x = a + b2       or      x = a - b2

                                     OR

     

    = 3x2 - 26x + 2 = 0⇒ 3x2 - 6x -  6x + 2 = 0⇒ 3 3x - 2 - 2 3x - 2 = 0⇒ 3x - 2 3x - 2 = 0⇒  3x - 22 = 0∴  3x - 2 = 0⇒  3x = 2⇒ x =  2 3⇒ x =  2 x  3 32⇒ x = 63

    Question 375
    CBSEENMA10009838
    Wired Faculty App

    A shopkeeper buys some books for Rs. 80. If he had bought 4 more books for the same amount, each book would have cost Rs. 1 less. Find the number of books he bought.


                                                OR


    The sum of two number is 9 and the sum of their reciprocals is 12. Find the numbers.
    Solution

    Total cost of books = Rs.80

    Let the number of books = x

    So the cost of each book = Rs 80x

    Cost of each book if he buy 4 more books = Rs 80x + 4

    As per given in equations:

     

    80x - 80x + 4 = 1⇒ 80x + 320 - 80xx( x + 4) = 1⇒  320x 2+ 4x = 1⇒ x2 + 4x - 320 = 0⇒ (x + 20) ( x- 16) = 0⇒ x = -20   or   x = 16

    Since number of books cannot be negative,

    so the number of books he brought is 16.

     

                                       OR

     

    Let the frist number be x then the second number be 9 - x as the sum of both  number is 9.

    Now the sum of their reciprocal is 12, therefor

     =  1x + 19 - x = 12⇒ 9 - x + xx( 9 - x ) = 12⇒ 99x - x2 = 12⇒  18= 9x - x2 ⇒  x2 - 9x + 18 = 0⇒  ( x- 6 ) ( x - 3 ) = 0⇒  x = 6   or   x = 3

    If  x = 6 then other number is 3.

    And, if x = 3 then other number is 6.

    Hence numbers are 3 and 6.

     

     

     

    Mock Test Series

    Sponsor Area

    Sponsor Area

    NCERT Book Store

    NCERT Sample Papers

    Entrance Exams Preparation

    20