Question
Represent the following problem situations in the form of quadratic equations:
The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
Solution
Let breadth of the rectangle = x m Then, length of the rectangle = (2x + 1) m
∵ Area of the rectangle = (2x + 1) x m2
According to the given condition,
(2x + 1)x = 528 ⇒ 2x2 + x – 528 = 0
which is a quadratic equation in x.
Solving this equation by factorisation method, we get
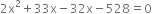





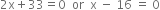


But breadth cannot be -ve.
∴ x = 16
Hence, breadth of the rectangle = 16 m and length of the rectangle = 2 x 16 + 1 = 33 m.
∵ Area of the rectangle = (2x + 1) x m2
According to the given condition,
(2x + 1)x = 528 ⇒ 2x2 + x – 528 = 0
which is a quadratic equation in x.
Solving this equation by factorisation method, we get
But breadth cannot be -ve.
∴ x = 16
Hence, breadth of the rectangle = 16 m and length of the rectangle = 2 x 16 + 1 = 33 m.





