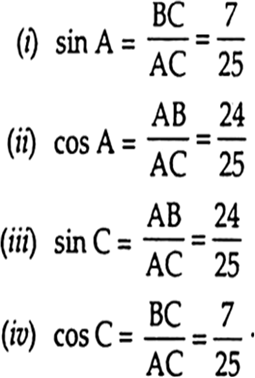Wiredfaculty Logo

For Daily Free Study Material Join wiredfaculty Whatsapp Group | Download Android App | Ncert Book Download

Mathematics Chapter 9 Some Applications Of Trigonometry

    • Sponsor Area

    NCERT Solution For Class 10 Mathematics

    Some Applications Of Trigonometry Here is the CBSE Mathematics Chapter 9 for Class 10 students. Summary and detailed explanation of the lesson, including the definitions of difficult words. All of the exercises and questions and answers from the lesson's back end have been completed. NCERT Solutions for Class 10 Mathematics Some Applications Of Trigonometry Chapter 9 NCERT Solutions for Class 10 Mathematics Some Applications Of Trigonometry Chapter 9 The following is a summary in Hindi and English for the academic year 2021-2022. You can save these solutions to your computer or use the Class 10 Mathematics.

    Question 1
    CBSEENMA10007606
    Wired Faculty App

    In ΔABC, right angled at B. AB = 24 cm, BC = 7 cm. Determine:
    (i) sin A cos A,
    (ii) sin C, cos C.

    Solution

    Let AB = 24 cm
    BC = 7cm Using Pythagoras theorem, we have
    AC2 = AB2 + BC2
    = (24 cm)2+ (7 cm)2
    = 576 cm2 + 49 cm2
    = 625 cm2
    So, AC = 25 cm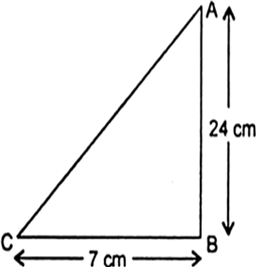

    Now,

    Question 2
    CBSEENMA10007607
    Wired Faculty App

    In the given figure, find tan P - cot R.

    Solution

    Let
    PQ = 12K
    and
    PR = 13K
    Using Pythagoras theorem, we have
    PR2 = PQ2 + QR2
    ⇒(13K)2 = (12K)2 + QR2
    ⇒169K2 = 144K2 + QR2
    ⇒QR2 = 169K2 - 144K2
    ⇒QR2 = 25K2
    So, QR = 5K

    Now, 
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Therefore,
    tanP minus cotR space equals space 5 over 12 minus 5 over 12 equals 0.

    Question 3
    CBSEENMA10007608
    Wired Faculty App

    If sinA space equals space 3 over 4 comma space calculate cos A and tan A.
    Solution
    Let us draw a right angle triangle, right angled at B.
    We know that:
    space sin space straight A space equals space 3 over 4 space equals space BC over AC
     Let BC = 3K,  AC = 4K
    where K is a positive number.

    Using Pythagoras theorem, we have
                     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow        space space space space space space left parenthesis 4 straight K right parenthesis squared space equals space AB squared plus left parenthesis 3 straight K right parenthesis squared
    rightwards double arrow              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow              space AB squared space equals space 16 straight K squared minus 9 straight K squared
    rightwards double arrow               <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow               <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Now,  cosA space equals space AB over AC equals fraction numerator square root of 7 straight K over denominator 4 straight K end fraction space equals fraction numerator square root of 7 over denominator 4 end fraction
    and    tanA space equals space BC over AB equals fraction numerator 3 straight K over denominator square root of 7 straight K end fraction equals fraction numerator 3 over denominator square root of 7 end fraction.
    Question 4
    CBSEENMA10007609
    Wired Faculty App

    Given 15 cot A = 8, find sin A and sec A.

    Solution
    Let us draw a right triangle ABC, right angled at B.
    It is given that:
    15 cot A = 8
    rightwards double arrow              space space cotA space equals space 8 over 15 equals AB over BC

    Let
    AB = 8K, BC = 15K
    Using Pythagoras theorem, we have
    AC2 = AB2 + BC2 = (8K)2 + (15K)2
    = 64K2 + 225K2
    = 289K2
    So,
    AC = 17K
    Now,
    AC = 17K
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 5
    CBSEENMA10007610
    Wired Faculty App

    Given space secθ space equals space 13 over 12 comma space  calculate all other trigonometric ratios.
    Solution
    Let us draw a right angle triangle, right angled at B.
    We know that:
      secθ space equals space 13 over 12 equals AC over AB
    Let AB = 12 K,   AC = 13K
    where K is a positive number.

    Using Pythagoras theorem, we have
    AC2 = AB2 + BC2
    ⇒(13 K)2 = (12 K)2 + BC2
    ⇒169 K2 = 144 K2 + BC2
    ⇒BC2 = 169 K2-144 K2
    BC2 = 25 K2 rightwards double arrow BC = 5 K.
    Now, 

    and cosecθ space equals space AC over BC equals fraction numerator 13 straight K over denominator 5 straight K end fraction equals 13 over 5.

    Question 6
    CBSEENMA10007611
    Wired Faculty App

    If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

    Solution
    Let us consider two right angle triangles right angled at Q and S respectively.
    Now,
    cosA space equals space AS over AR
    cosB space equals space BQ over BP
    But cos A = cos B (given)
    ∴           AS over AR equals BQ over BP
    rightwards double arrow        AS over BQ space equals space AR over BP
    Let         AS over BQ equals AR over BP equals straight K

    In ΔRAS,
    Using Pythagoras theorem, we have
    RS space equals space square root of AR squared minus AS squared end root space space space space space space space equals space square root of left parenthesis straight K times BP right parenthesis squared minus left parenthesis straight K. BQ right parenthesis squared end root space space space space space space space space equals space square root of left parenthesis straight K squared times BP squared minus straight K squared times BQ right parenthesis squared end root space space space space space space space equals space square root of straight K squared left parenthesis BP squared minus BQ squared right parenthesis end root space space space space space space equals space straight K square root of left parenthesis BP squared minus BQ squared right parenthesis end root
    In APBQ,
    Using Pythagoras theorem, we have
    PQ space equals space square root of BP squared minus BQ squared end root
    So, RS over PQ equals fraction numerator straight K. square root of BP squared minus BQ squared end root over denominator square root of BP squared minus BQ squared end root end fraction equals straight K space space... left parenthesis ii right parenthesis
    Comparing (i) and (ii), we get
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    So, by using SSS similar condition
                        space increment RSA space tilde space increment PQB
    ∴                           angle straight A space equals space angle straight B.
    Question 7
    CBSEENMA10007612
    Wired Faculty App

    If cot θ = 7 over 8 comma evaluate: 
    fraction numerator left parenthesis 1 plus sinθ right parenthesis space left parenthesis 1 minus sinθ right parenthesis over denominator left parenthesis 1 plus cosθ right parenthesis space left parenthesis 1 minus cosθ right parenthesis end fraction
    Solution
    Consider a right angle triangle, right angled at B and ∠ACB = θ.
    Here, space cotθ space equals space BC over AB space equals space 7 over 8
    BC = 7K
    Let BC = 7K
    AB = 8K
    Using Pythagoras theorem, we have
             <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
                        equals 64 straight K squared plus 49 straight K squared space equals space 113 straight K squared
    rightwards double arrow         AC space equals space square root of 113 straight K

    Now,
    sinθ space equals space AB over AC space equals space fraction numerator 8 straight K over denominator square root of 113 straight K end fraction equals fraction numerator 8 over denominator square root of 113 end fraction cosθ space equals space BC over AC space equals space fraction numerator 7 straight K over denominator square root of 113 straight K end fraction equals fraction numerator 7 over denominator square root of 113 end fraction
    Now, 
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
                                  space space equals space fraction numerator 1 minus open parentheses begin display style fraction numerator 8 over denominator square root of 113 end fraction end style close parentheses squared over denominator 1 minus open parentheses begin display style fraction numerator 7 over denominator square root of 113 end fraction end style close parentheses squared end fraction equals fraction numerator 1 minus begin display style 64 over 113 end style over denominator 1 minus begin display style 49 over 113 end style end fraction
                                     equals space fraction numerator begin display style fraction numerator 113 minus 64 over denominator 113 end fraction end style over denominator begin display style fraction numerator 113 minus 49 over denominator 113 end fraction end style end fraction equals 49 over 64.
                   
    Question 8
    CBSEENMA10007613
    Wired Faculty App

    If 3 cot A = 4, check whether
    fraction numerator 1 minus tan squared straight A over denominator 1 plus tan squared straight A end fraction equals cos squared straight A space minus space sin squared straight A or not.

    Solution
    Let us draw a right triangle right angled at B.
    We have,
    3 cot A = 4
    rightwards double arrow                 cotA space equals space 4 over 3 space equals space AB over BC
    Let AB = 4K and BC = 3K

    Using Pythagoras theorem, we have
    AC2 = AB2 + BC2
    = (4K)2 + (3K)2
    = 16K2 + 9K2 = 25 K2
    So, AC = 5K
    tan space straight A space equals space BC over AB space equals space fraction numerator 3 straight K over denominator 4 straight K end fraction space equals space 3 over 4
    Now, <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    and sinA space equals space BC over AC equals fraction numerator 3 straight K over denominator 5 straight K end fraction space equals space 3 over 5
         L.H.S. = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
                  space space equals space fraction numerator 1 minus open parentheses begin display style 3 over 4 end style close parentheses squared over denominator 1 plus open parentheses begin display style 3 over 4 end style close parentheses squared end fraction space equals space fraction numerator 1 minus begin display style 9 over 16 end style over denominator 1 plus begin display style 9 over 16 end style end fraction
                     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Now, 
    R.H.S. = cos squared straight A space minus space sin squared straight A
               equals space open parentheses 4 over 5 close parentheses squared minus open parentheses 3 over 5 close parentheses squared equals space 16 over 25 minus 9 over 25 space equals space fraction numerator 16 minus 9 over denominator 25 end fraction space equals space 7 over 25
    Hence, L.H.S. = R.H.S.
    or space fraction numerator 1 minus tan squared straight A over denominator 1 plus tan squared straight A end fraction equals cos squared straight A space minus space sin squared straight A.

    Question 9
    CBSEENMA10007614
    Wired Faculty App

    In triangle ABC, right angled at B, if <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> find the value of :
    (i) sin A cos C + cos A sin C 
    (ii) cos A .cos C - sin A.sin C.

    Solution

    We have,
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Let <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Using Pythagoras theorem, we have
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    AC = 2K
    So,
    AC = 2K

       space sin space straight A space equals space BC over AC equals fraction numerator straight K over denominator 2 straight K end fraction equals 1 half space sin space straight C space equals space AB over AC equals fraction numerator square root of 3 straight K over denominator 2 straight K end fraction equals fraction numerator square root of 3 over denominator 2 end fraction Now comma space cos space straight A space equals space AB over AC space equals space fraction numerator square root of 3 straight K over denominator 2 straight K end fraction equals fraction numerator square root of 3 over denominator 2 end fraction
    and , cos space straight C space equals space BC over AC equals fraction numerator straight K over denominator 2 straight K end fraction equals 1 half
    Now,
    (i) sin A cos C + cos A sin C
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    (ii) cos A. cos C - sin A .sin C
    equals space fraction numerator square root of 3 over denominator 2 end fraction cross times 1 half minus 1 half cross times fraction numerator square root of 3 over denominator 2 end fraction equals space fraction numerator square root of 3 over denominator 4 end fraction minus fraction numerator square root of 3 over denominator 4 end fraction space equals space 0.

    Question 10
    CBSEENMA10007615
    Wired Faculty App

    In ΔPQR, right angled at Q. PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.

    Solution

     We have,
    Let
    PR + QR = 25 cm ..(i)
    PR = x cm
    QR = (25 - x) cm.
    Using Pythagoras theorem, we have
    PR2 = PQ2 + RQ2
    ⇒x2 = (5Y + (25 - x)2
    x2 = 25 + 625 + x2 - 50x
    ⇒50x = 650
    ⇒x = 13 cm
     

    Now,
    PR = x = 13 cm QR = (25 - x) = 12 cm
    and
    PQ = 5 cm
    Now,
    PQ = 5 cm
    sin space straight P space equals space RQ over PR space equals space 12 over 13. CosP space equals space PQ over PR space equals space 5 over 13.
    and <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 11
    CBSEENMA10007616
    Wired Faculty App

    State whether the following are true or false. Justify your answer.
    (i) The value of tan A is always less than 1.
    (ii) sec A = 12/5 for some value of angle A.
    (iii) cos A is the abbreviation used for the cosecant of angle A.
    (iv) cot A is the product of cot and A.
    (v) sin θ= 4/3 for some angle 6.

    Solution

    (i) False, since space tanA space equals space Perpendicular over Base and perpendicular may  be longer than base.
    (ii) True, since <pre>uncaught exception: <b>file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/35/96/ec5690fd6e7cbf9b256641ccf1bd.ini): failed to open stream: Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php at line #12file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/35/96/ec5690fd6e7cbf9b256641ccf1bd.ini): failed to open stream: Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php line 12<br />#0 [internal function]: _hx_error_handler(2, 'file_put_conten...', '/home/config_ad...', 12, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php(12): file_put_contents('/home/config_ad...', 'mml=<math xmlns...') #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(48): sys_io_File::saveContent('/home/config_ad...', 'mml=<math xmlns...') #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(112): com_wiris_util_sys_Store->write('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #6 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #7 {main}</pre> and hypotenuse being the longest side may be times the base.
    (iii) False, since cos A is the abbreviation used for the cosine of angle A.
    (iv) False, since cot A is used as an abbreviation for 'the cotangent of the angle A'.
    (v) False, since the hypotenuse is the longest side in a right triangle. As such the value of sin A is always less than 1 (or, in particular equal to 1).

    Question 12
    CBSEENMA10007617
    Wired Faculty App

    Evaluate:
    sin 60° cos 30° + sin 30° cos 60°

    Solution
    sin 60°. cos 30° + sin 30°. cos 60°
    = fraction numerator square root of 3 over denominator 2 end fraction cross times fraction numerator square root of 3 over denominator 2 end fraction plus 1 half cross times 1 half
    equals space open parentheses fraction numerator square root of 3 over denominator 2 end fraction close parentheses squared plus open parentheses 1 half close parentheses squared
    equals space 3 over 4 plus 1 fourth equals space fraction numerator 3 plus 1 over denominator 4 end fraction equals 4 over 4 equals 1.
    Question 13
    CBSEENMA10007618
    Wired Faculty App

    Evaluate:
    2 tan2 45° + cos2 30° - sin2 60°

    Solution
    2 tan2 45° + cos2 30° - sin2 60°
    equals space 2 left parenthesis 1 right parenthesis squared plus open parentheses fraction numerator square root of 3 over denominator 2 end fraction close parentheses squared minus open parentheses fraction numerator square root of 3 over denominator 2 end fraction close parentheses squared equals space 2 plus 3 over 4 minus 3 over 4 space equals space 2.
    Question 14
    CBSEENMA10007623
    Wired Faculty App

    Evaluate:
    fraction numerator cos space 45 degree over denominator sec space 30 degree space plus space cosec space 30 degree end fraction.

    Solution
    fraction numerator cos space 45 degree over denominator sec space 30 degree plus cosec space 30 degree end fraction
    equals space fraction numerator begin display style fraction numerator 1 over denominator square root of 2 end fraction end style over denominator begin display style fraction numerator 2 over denominator square root of 3 end fraction end style plus begin display style 2 over 1 end style end fraction space equals space fraction numerator begin display style fraction numerator 1 over denominator square root of 2 end fraction end style over denominator begin display style fraction numerator 2 plus 2 square root of 3 over denominator square root of 3 end fraction end style end fraction
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #57mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 57<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 57, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(57): mkdir('/home/config_ad...', 511) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    equals space fraction numerator 2 square root of 6 minus 2 square root of 18 over denominator 8 minus 24 end fraction equals fraction numerator 2 square root of 6 minus 6 square root of 2 over denominator negative 16 end fraction equals space fraction numerator 2 left parenthesis square root of 6 minus 3 square root of 2 right parenthesis over denominator negative 16 end fraction equals fraction numerator 3 square root of 2 minus square root of 6 over denominator 8 end fraction.
    Question 17
    CBSEENMA10007639
    Wired Faculty App

    Choose the correct option and justify your choice:
    sin 2A = 2 sin A is true when A = 
    (A) 0°         (B) 30°         (C) 45°       (D) 60°
    Solution

    (iii) If A = 0
    Then, L.H.S. = sin 2A = sin 2(0)
    = sin 0° = 0
    R.H.S. = 2 sin A = 2 sin 0°
    = 2 x 0 = 0
    Ans. (A).

    Sponsor Area

    Question 19
    CBSEENMA10007657
    Wired Faculty App

    If tan left parenthesis straight A plus straight B right parenthesis space equals square root of 3 space space and space tan left parenthesis straight A minus straight B right parenthesis space equals space fraction numerator 1 over denominator square root of 3 end fraction semicolon 0 degree less than straight A plus straight B less or equal than 90 degree semicolon space space space straight A greater than straight B. Find A and B.
    Solution
    tan left parenthesis straight A plus straight B right parenthesis space equals space square root of 3
    ⇒A + B = 60° ...(i)
    and
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #57mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 57<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 57, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(57): mkdir('/home/config_ad...', 511) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    ⇒A-B = 30° ...(ii)
    Solving (i) and (ii), we get
    A = 45° and B = 15°.
    Question 20
    CBSEENMA10007658
    Wired Faculty App

    State whether the following are true false. Justify your answer.
    sin (A + B) = sin A + sin B.

    Solution
     Take A = 30° and B = 30°.
    Then sin (A + B) = sin (30°+ 30°)
    equals sin 60 degree space equals space fraction numerator square root of 3 over denominator 2 end fraction
    and sin A + sin B = sin 30° + sin 30°
    equals 1 half plus 1 half equals 1
    So, sin (A + B) ≤θ sin A + sin B.
    Hence, this statement is false.
    Question 21
    CBSEENMA10007659
    Wired Faculty App

    State whether the following are true false. Justify your answer.
    The value of sin θ increases as θ increases.

    Solution
    True as it is clear form the ready reference table.
    Question 22
    CBSEENMA10007660
    Wired Faculty App

    State whether the following are true false. Justify your answer.
    The value of cos θ increases as θ increases.

    Solution
    False as we observe from the ready reference table that the value of cosθ decreases as θ increases.
    Question 23
    CBSEENMA10007661
    Wired Faculty App

    State whether the following are true false. Justify your answer.
    sin θ = cos θ for all values of θ.

    Solution

    Take straight theta space equals space 60 degree
    Then sinθ space equals space sin 60 degree space equals space fraction numerator square root of 3 over denominator 2 end fraction
    and cosθ space equals space cos space 60 degree space equals space 1 half
    So, sin θ ≤θ cos θ
    Hence, this statement is false.

    Question 24
    CBSEENMA10007662
    Wired Faculty App

    State whether the following are true false. Justify your answer.
    cot A is not defined for A = 0°.

    Solution
    True as it is clear from the ready reference table.
    Question 25
    CBSEENMA10007663
    Wired Faculty App

    Evaluate:
    fraction numerator sin space 18 degree over denominator cot space 72 degree end fraction

    Solution
    fraction numerator sin space 18 degree over denominator cot space 72 degree end fraction space equals space fraction numerator sin space left parenthesis 90 degree minus 72 degree right parenthesis over denominator cos space 72 degree end fraction space equals space fraction numerator cos space 72 degree over denominator cot space 72 degree end fraction space space space space space space space space space space space space space space space space space space equals space 1. space space space space space space space space space space space space space space space space space space space space space space space space space left square bracket because space space sin space left parenthesis 90 degree minus straight theta right parenthesis space equals space cos space straight theta right square bracket
    Question 26
    CBSEENMA10007665
    Wired Faculty App

    Evaluate:
    fraction numerator tan space 26 degree over denominator cot space 64 degree end fraction

    Solution
    fraction numerator tan space 26 degree over denominator cot space 64 degree end fraction equals fraction numerator tan thin space left parenthesis 90 degree minus 64 degree right parenthesis over denominator cot space 64 degree end fraction space equals space fraction numerator cot space 64 degree over denominator cot space 64 degree end fraction space equals space 1 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left square bracket space because space space tan space left parenthesis 90 degree minus straight theta right parenthesis space equals space cosθ right square bracket
    Question 27
    CBSEENMA10007666
    Wired Faculty App

    Evaluate:
    cos space 48 degree space minus space sin space 42 degree

    Solution

    cos 48° - sin 42°
    = cos (90° - 42°) - sin 42° = sin 42° - sin 42° = 0.

    Question 28
    CBSEENMA10007667
    Wired Faculty App

    Evaluate:
    cosec space 31 degree space minus space sec space 59 degree.

    Solution

    cosec 31° - sec 59°
    = cosec (90°-59°)-sec 59°
    = sec 59° - sec 59° = 0.

    Question 29
    CBSEENMA10007669
    Wired Faculty App

    Show that:
    tan 48° tan 23° tan 42° tan 67° = 1.
    Solution

    LHS
    = tan 48° . tan 23°. tan 42° . tan 67°
    = tan 48° . tan 42° . tan 23° . tan 67°
    = tan (90° - 42°). tan 42°. tan (90° - 67°). tan 67°
    = cot 42° . tan 42° . cot 67° . tan 67°
    = 1 x 1 = 1 = RHS Proved.

    Question 30
    CBSEENMA10007675
    Wired Faculty App

    Show that:
    cos 38° cos 52° - sin 38° sin 52° = 0.
    Solution

    LHS
    = cos 38° . cos 52° - sin 38° . sin 52°
    = cos (90°-52°). cos 52°-sin (90° - 52°). sin 52°
    = sin 52° . cos 52° - cos 52° . sin 52°
    = 0 = RHS Proved.

    Question 31
    CBSEENMA10007678
    Wired Faculty App

    If tan 2A = cot (A - 18°), where 2A is an acute angle, find the value of A.

    Solution

    tan 2A = cot (A - 18°) =
    rightwards double arrow cot (90° - 2A) = cot (A-18°)
    ⇒90° - 2A = A - 18°
    ⇒-3A = -108°
    ⇒A = 36°.

    Question 32
    CBSEENMA10007680
    Wired Faculty App

    If tan A = cot B, prove that A + B = 90°. 

    Solution
    We have,
    tan A = cot B ⇒ cot (90° - A) = cot B
    ⇒90° - A = B
    ⇒90° = A + B or A + B = 90°
    Question 33
    CBSEENMA10007682
    Wired Faculty App

    If sec 4A = cosec (A - 20°), where 4A is an acute angle, find the value of A.

    Solution

    We have,
    sec 4A = cosec (A - 20°)
    cosec (90° - 4A) = cosec (A - 20°)
    ⇒90° - 4A = A - 20°
    ⇒-5 A = -110°
    ⇒A = 22°.

    Question 34
    CBSEENMA10007687
    Wired Faculty App

    If A, B and C are interior angles of ΔABC, then show that
              space sin space open parentheses fraction numerator straight B plus straight C over denominator 2 end fraction close parentheses space equals space cos straight A over 2.

    Solution
     In ΔABC, we have
                straight A plus straight B plus straight C space equals space 180 degree
    rightwards double arrow space space space space space space space space space space space space space space space space space space space straight B plus straight C space equals space 180 degree space space minus straight A rightwards double arrow space space space space space space space space space space space space space space space space space space space fraction numerator straight B plus straight C over denominator 2 end fraction space equals space 90 degree minus straight A over 2 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left square bracket dividing space both space side space by space 2 right square bracket
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #57mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 57<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 57, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(57): mkdir('/home/config_ad...', 511) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 35
    CBSEENMA10007690
    Wired Faculty App

    Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.

    Solution

    sin 67° + cos 75°
    = sin (90° - 23°) + cos (90° - 15°) = cos 23° + sin 15°.

    Question 36
    CBSEENMA10007695
    Wired Faculty App

    Express the trigonometric ratios sin A sec A, and tan A in terms of cot A.

    Solution
    cot squared straight A space plus space 1 space equals cosec squared straight A
    rightwards double arrow            <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #57mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 57<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 57, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(57): mkdir('/home/config_ad...', 511) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    This gives <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #57mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 57<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 57, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(57): mkdir('/home/config_ad...', 511) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Hence,      sinA space equals space 1 over cosecA equals fraction numerator 1 over denominator square root of cot squared straight A plus 1 end root end fraction
                     secA space equals space 1 over cosA space equals space cosecA over cotA
                                equals space fraction numerator square root of cot squared straight A plus 1 end root over denominator cotA end fraction
    and  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #57mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 57<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 57, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(57): mkdir('/home/config_ad...', 511) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 38
    CBSEENMA10007714
    Wired Faculty App

    Evaluate:
    fraction numerator sin squared 63 degree plus sin squared 27 degree over denominator cos squared 17 degree plus cos squared 73 degree end fraction.

    Solution
    fraction numerator sin squared left parenthesis 90 degree minus 27 degree right parenthesis plus sin squared 27 degree over denominator cos squared left parenthesis 90 degree minus 73 degree right parenthesis plus cos squared 73 degree end fraction
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    [Using sin2 A + cos2 A = 1]
    space equals space 1 over 1 equals 1
    Question 39
    CBSEENMA10007717
    Wired Faculty App

    Evaluate:
    Solution

    sin (90° - 65°). cos 65° + cos (90° - 65°). sin 65°
    = cos65°. cos 65° + sin 65° sin 65°
    = cos2 65° + sin2 65° [Using sin2 A + cos2 A = 1]
    = 1.

    Sponsor Area

    Question 43
    CBSEENMA10007732
    Wired Faculty App

    Choose the correct option and Justify your choice.
    space fraction numerator 1 plus tan squared straight A over denominator 1 plus cot squared straight A end fraction equals
    (A) sec squared straight A      (B) -1     (C) cot squared straight A     (D) tan squared straight A

    Solution
    fraction numerator 1 plus tan squared straight A over denominator 1 plus cot squared straight A end fraction space equals space fraction numerator sec squared straight A over denominator cosec squared straight A end fraction
                        equals space fraction numerator begin display style fraction numerator 1 over denominator cos squared straight A end fraction end style over denominator begin display style fraction numerator 1 over denominator sin squared straight A end fraction end style end fraction space equals space fraction numerator 1 over denominator cos squared straight A end fraction cross times fraction numerator sin squared straight A over denominator 1 end fraction
                        equals space fraction numerator sin squared straight A over denominator cos squared straight A end fraction space equals space tan squared straight A.
    Hence, correct option is (D).
    Question 44
    CBSEENMA10007734
    Wired Faculty App

    Prove the following identities where the angles involved are acute angles for which the expressions are defined.
    space space left parenthesis cosecθ space minus space cotθ right parenthesis squared space equals space fraction numerator 1 minus cosθ over denominator 1 plus cosθ end fraction.

    Solution
    left parenthesis cosecθ minus cotθ right parenthesis squared space equals space fraction numerator 1 minus cosθ over denominator 1 plus cosθ end fraction
    L.H.S. = left parenthesis cosecθ space minus space cotθ right parenthesis squared
               = open parentheses 1 over sinθ minus cosθ over sinθ close parentheses squared
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    equals space fraction numerator left parenthesis 1 minus cosθ right parenthesis squared over denominator sin squared straight theta end fraction equals space fraction numerator left parenthesis 1 minus cosθ right parenthesis squared over denominator 1 minus cos squared straight theta end fraction
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Hence, L.H.S. = R.H.S.
    Question 47
    CBSEENMA10007744
    Wired Faculty App

    Prove the following identities where the angles involved are acute angles for which the expressions are defined.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    fraction numerator 1 plus secA over denominator secA end fraction equals fraction numerator sin squared straight A over denominator 1 minus cosA end fraction
    L.H.S. = fraction numerator 1 plus secA over denominator secA end fraction

             equals space fraction numerator 1 plus begin display style 1 over cosA end style over denominator begin display style 1 over cosA end style end fraction space equals space fraction numerator begin display style fraction numerator cosA plus 1 over denominator cosA end fraction end style over denominator begin display style 1 over cosA end style end fraction
              <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    R.H.S. = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
               equals space fraction numerator left parenthesis 1 plus cosA right parenthesis thin space left parenthesis 1 minus cosA right parenthesis over denominator left parenthesis 1 minus cosA right parenthesis end fraction equals space 1 plus space cosA
    Hence, L.H.S. = R.H.S. ALTERNATIVE METHOD:
     straight R. straight H. straight S. equals fraction numerator sin squared straight A over denominator 1 minus cosA end fraction equals fraction numerator 1 minus cos squared straight A over denominator 1 minus cosA end fraction space space space space space space space space space space space space equals space fraction numerator left parenthesis 1 plus cosA right parenthesis space left parenthesis 1 minus cosA right parenthesis over denominator left parenthesis 1 minus cosA right parenthesis end fraction space space space space space space space space space space space equals space 1 plus space cosA space equals space 1 plus 1 over secA space space space space space space space space space space equals space fraction numerator secA space plus space 1 over denominator secA end fraction space equals space fraction numerator 1 plus secA over denominator secA end fraction space space space space space space space space equals straight R. straight H. straight S comma space space Hence comma space space straight L. straight H. straight S. space equals space space straight R. straight H. straight S.
    Question 48
    CBSEENMA10007750
    Wired Faculty App

    Prove the following identities where the angles involved are acute angles for which the expressions are defined.
    fraction numerator cos space straight A minus sin space straight A plus 1 over denominator cos space straight A plus sin space straight A minus 1 end fraction equals cosec space straight A plus cot space straight A.

    Solution
    fraction numerator cosA minus sinA plus 1 over denominator cosA plus sinA minus 1 end fraction space equals space cosecA plus cotA
               L.H.S. = fraction numerator cosA minus sinA plus 1 over denominator cosA plus sinA minus 1 end fraction
    Dividing N' and D' by sin A, we get
                          space equals space fraction numerator begin display style fraction numerator cosA minus sinA plus 1 over denominator sinA end fraction end style over denominator begin display style fraction numerator cosA plus sinA minus 1 over denominator sinA end fraction end style end fraction

                    space space space space equals space fraction numerator begin display style cosA over sinA minus sinA over sinA plus 1 over sinA end style over denominator begin display style cosA over sinA plus sinA over sinA minus 1 over sinA end style end fraction
                     equals space fraction numerator cotA minus 1 plus cosecA over denominator cotA plus 1 minus cosecA end fraction equals space fraction numerator cotA plus cosecA minus 1 over denominator cotA minus cosecA plus 1 end fraction equals space fraction numerator left parenthesis cotA plus cosecA right parenthesis minus left parenthesis cosec squared straight A minus cot squared straight A right parenthesis over denominator cotA minus cosecA plus 1 end fraction equals space fraction numerator left parenthesis cotA plus cosecA right parenthesis minus left parenthesis cosecA plus cotA right parenthesis space left parenthesis cosecA minus cotA right parenthesis over denominator cotA minus cosecA plus 1 end fraction equals space fraction numerator left parenthesis cotA plus cosecA right parenthesis left parenthesis 1 minus cosecA plus cotA right parenthesis over denominator left parenthesis cotA minus cosecA plus 1 right parenthesis end fraction equals space cot space straight A space plus space cosec space straight A space equals space straight R. straight H. straight S. space Hence comma space straight L. straight H. straight S. space equals space straight R. straight H. straight S.
                 
                       
    Question 50
    CBSEENMA10007831
    Wired Faculty App

    Prove the following identities where the angles involved are acute angles for which the expressions are defined.
    fraction numerator sinθ minus 2 sin cubed straight theta over denominator 2 cos cubed straight theta minus cosθ end fraction equals space space tanθ

    Solution
    straight L. straight H. straight S. equals fraction numerator sinθ minus 2 sin cubed straight theta over denominator 2 cos cubed straight theta minus cosθ end fraction
               equals fraction numerator sinθ left parenthesis 1 minus 2 sin squared straight theta right parenthesis over denominator cosθ left parenthesis 2 cos squared straight theta minus 1 right parenthesis end fraction
      equals sinθ over cosθ cross times open square brackets fraction numerator left square bracket 1 minus 2 left parenthesis 1 minus cos squared straight theta right parenthesis right square bracket over denominator 2 cos squared straight theta minus 1 end fraction close square brackets equals space tanθ space. space open square brackets fraction numerator 1 minus 2 plus 2 cos squared straight theta over denominator 2 cos squared straight theta minus 1 end fraction close square brackets equals space tanθ space cross times space open parentheses fraction numerator 2 space cos squared straight theta minus 1 over denominator 2 space cos squared space straight theta space minus 1 end fraction close parentheses equals space tanθ space equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
    Question 51
    CBSEENMA10007832
    Wired Faculty App

    Prove the following identities where the angles involved are acute angles for which the expressions are defined.
    (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2A + cot2A

    Solution

    (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2A + cot2 A
    L.H.S.
    = (sin A + cosec A)2 + (cos A + sec A)2
    = (sin2 A + cosec2 A + 2 sin A. cosec A + cos2 A + sec2 A + 2 cos A. sec A
    = (sin2 A + cos2 A) + 2 sin A. cosec A + 2 cos A. sec A + cosec2 A + sec2 A
    = 1 + 2 + 2 + (cot2 A + 1) + (tan2 A + 1)
    = 5 + 1 + 1 + cot2 A + tan2 A
    = 7 + tan2 A + cot2 A = R.H.S.
    Hence, L.H.S. = R.H.S.

    Question 54
    CBSEENMA10007837
    Wired Faculty App

    Write the value of sin2 69° + sin2 21°. 

    Solution

    sin2 69° + sin2 21° = sin2 (90 - 21°) + sin2 21°
    = cos2 21° +sin2 21° = 1. 1

    Question 55
    CBSEENMA10007838
    Wired Faculty App

    If sin θ = 1/3, then find the value of (2 cot2θ+ 2).

    Solution
     2cot2 θ + 2 =2 (cosec2θ - 1) + 2
    = 2 cosec2 θ -2 + 2
    = 2 cosec2 θ
    fraction numerator 2 over denominator sin squared straight theta end fraction space equals space fraction numerator 2 over denominator 1 divided by 9 end fraction space space equals space 18.
    Question 56
    CBSEENMA10007839
    Wired Faculty App

    In ΔABC, ∠B = 90°
    3 sin A = 3/5 , what is the value cos C.

    Solution
    We have, ∠B = 90°
    and
    sinA space equals space 3 over 5 space equals space BC over AC
    Now,
    cosC space equals space BC over AC equals 3 over 5

    Question 57
    CBSEENMA10007840
    Wired Faculty App

    If 15 cot θ = 8, then find the value of
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    We have,
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Now,    space fraction numerator left parenthesis 1 minus sinθ right parenthesis thin space left parenthesis 1 plus sin space straight theta right parenthesis over denominator left parenthesis 1 plus cosθ right parenthesis thin space left parenthesis 1 minus cosθ right parenthesis end fraction space equals space fraction numerator 1 minus sin squared straight theta over denominator 1 minus cos squared straight theta end fraction
    equals space fraction numerator cos squared straight theta over denominator sin squared straight theta end fraction space equals space cot squared straight theta space equals space open parentheses 8 over 15 close parentheses squared space equals space 64 over 225 Ans.
    Question 58
    CBSEENMA10007841
    Wired Faculty App

    Simplify:  fraction numerator sin cubed straight theta plus cos cubed straight theta over denominator sinθ plus cosθ end fraction plus sinθ. space cosθ
    Solution
    fraction numerator sin cubed straight theta plus cos cubed straight theta over denominator sinθ plus cosθ end fraction plus sinθ. cosθ
    equals space fraction numerator left parenthesis sinθ plus cosθ right parenthesis space left parenthesis sin squared straight theta plus cos squared straight theta minus sinθ. cosθ right parenthesis over denominator left parenthesis siinθ plus cosθ right parenthesis end fraction
                                                     plus sinθ. space cosθ
                            [∴ <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>]
    = (1 - sinθ cosθ) + sinθ. cosθ [∴ sin2θ + cos2θ = I ] = 1.Ans.
    Question 59
    CBSEENMA10007842
    Wired Faculty App

    Write the value of sin (65° + θ) -cos (25° - θ).

    Solution

    sin (65° + θ ) - cos (25° - θ)
    = cos [90° - (65° + θ)] - cos (25° - θ)
    = cos (90° - 65° - θ) - cos (25° - θ)
    = cos (25° - θ) - cos (25° - θ) = 0.

    Question 60
    CBSEENMA10007843
    Wired Faculty App

    Write the value of fraction numerator 5 over denominator cot squared straight theta end fraction minus fraction numerator 5 over denominator cos squared straight theta end fraction.

    Solution
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 61
    CBSEENMA10007844
    Wired Faculty App

    Express sin 84° + tan 59°, in terms of trigonometric ratio of angle between 0° and 45°.

    Solution

    sin 84° + tan 59°
    = sin (90° -6°) + tan (90° -31°) = cos 6° + cot 31°.

    Question 62
    CBSEENMA10007845
    Wired Faculty App

    In ΔABC, write cos fraction numerator straight B plus straight C over denominator 2 end fraction in terms of angle A.

    Solution
    cos space fraction numerator straight B plus straight C over denominator 2 end fraction space equals space cos open parentheses fraction numerator 180 degree minus straight A over denominator 2 end fraction close parentheses equals space cos space open parentheses fraction numerator 180 degree over denominator 2 end fraction minus straight A over 2 close parentheses space equals space cos open parentheses 90 degree minus straight A over 2 close parentheses space equals space sin straight A over 2
    Question 63
    CBSEENMA10007846
    Wired Faculty App

    Express tan A in terms of sin A.

    Solution
    space tanA space equals space fraction numerator sin space straight A over denominator cos space straight A end fraction space equals space fraction numerator sinA over denominator square root of 1 minus sin squared straight A end root end fraction.
    Question 64
    CBSEENMA10007847
    Wired Faculty App

    Without using trigonometric tables, evaluate:
    fraction numerator 7 space cos space 70 degree over denominator 2 space sin space 20 degree end fraction plus 3 over 2 fraction numerator space cos 55 degree. cosec 35 degree over denominator tan space 5 degree. space tan 45 degree. space tan 85 degree. space tan 65 degree end fraction

    Solution
    fraction numerator 7 space cos 70 degree over denominator 2 space sin space 20 degree end fraction plus 3 over 2 fraction numerator cos 55 degree space. space cosec space 35 degree over denominator tan space 5 degree space tan space 25 degree space tan 45 degree space. space tan 85 degree. space tan space 65 degree end fraction equals space fraction numerator 7 space cos left parenthesis 90 degree minus 20 degree right parenthesis over denominator 2 space sin space 20 degree end fraction plus 3 over 2 fraction numerator cos space left parenthesis 90 degree minus 35 degree right parenthesis. space cosec space 35 degree over denominator tan left parenthesis 90 degree minus 85 degree right parenthesis. space tan space 85 degree space. space tan space left parenthesis 90 degree space minus 65 degree right parenthesis. space tan space 65 degree space cross times space 1 end fraction equals space fraction numerator 7 sin space 20 degree over denominator 2 sin space 20 degree end fraction plus 3 over 2 fraction numerator sin 35 degree. cosec 35 degree over denominator cot space 85 degree. space tan 85 degree. space cot space 65 degree. space tan space 65 degree end fraction equals space 7 over 2 plus 3 over 2 space equals space 10 over 2 space equals space 5.
    Question 65
    CBSEENMA10007848
    Wired Faculty App

    If sin θ = cos θ, then write the value of θ. 0°<θ<90°.

    Solution

    sin θ = cos θ
    ⇒ cos (90-θ) = cos θ
    ⇒90-θ = θ
    ⇒2θ = 90 ⇒ θ = 45°.

    Question 66
    CBSEENMA10007849
    Wired Faculty App

    Write the value of 3 cos 52°. cos 38° - 3 sin 52°. sin 38°.°°

    Solution

    = 3 cos (90° - 38°). cos 38°
    =3 sin (90°-38°). sin 38°
    = 3 sin 38° . cos 38° - 3 cos 38° . sin 38°
    = 0.

    Question 67
    CBSEENMA10007850
    Wired Faculty App

    Write the simplest value of 
    sinθ over cosecθ plus cosθ over secθ.

    Solution
    sinθ over cosecθ plus cosθ over secθ space equals space sinθ space times space fraction numerator 1 over denominator cosec space straight theta end fraction plus space cosθ. space 1 over secθ equals space sin squared straight theta space plus space cos squared straight theta space equals space 1.
    Question 69
    CBSEENMA10007853
    Wired Faculty App

    Evaluate:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    space fraction numerator tan space 65 degree over denominator cot space 25 degree end fraction space equals space fraction numerator tan left parenthesis 90 degree minus 25 degree right parenthesis over denominator cot space 25 degree end fraction space equals space fraction numerator cot space 25 degree over denominator cot space 25 degree end fraction space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left square bracket because space left parenthesis tan space left parenthesis 90 degree minus straight theta right parenthesis space equals space cot space straight theta right square bracket space space space space space space space space space space space space space space space space space space space space equals space 1.
    Question 70
    CBSEENMA10007855
    Wired Faculty App

    Evaluate:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    fraction numerator tan space 34 degree over denominator cot space 56 degree end fraction space equals space fraction numerator tan left parenthesis 90 degree minus 56 degree right parenthesis over denominator cot 56 degree end fraction space equals space fraction numerator cot space 56 degree over denominator cot space 56 degree end fraction space equals space 1.
    Question 71
    CBSEENMA10007857
    Wired Faculty App

    Evaluate:
    sin 38° - cos 52°.

    Solution

    sin 38° - cos 52°.
                         = sin (90° - 52°) - cos 52°
                         = cos 52° - cos 52° = 0

    Question 72
    CBSEENMA10007858
    Wired Faculty App

    Evaluate:
    sin 25° - cos 65°

    Solution

    sin 25° - cos 65°.
                         = sin (90° - 65°) - cos 65°
                         = cos 65° - cos 65° = 0.

    Question 73
    CBSEENMA10007860
    Wired Faculty App

    Evaluate:
    cot 34° - tan 56°

    Solution
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 74
    CBSEENMA10007861
    Wired Faculty App

    Evaluate:
     cosec25°-sec65°.

    Solution

     cosec25°-sec65°
                  equals space cosec left parenthesis 90 degree space minus space 65 degree right parenthesis space minus sec space 65 degree equals space sec space 65 degree space minus space sec space 65 degree space equals space 0. space

    Question 75
    CBSEENMA10007863
    Wired Faculty App

    Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.

    Solution

    cot 85° + cos 75°
    = cot (90° - 5°) + cos (90° - 15°)
    = tan 5° + sin 15°.

    Question 76
    CBSEENMA10007864
    Wired Faculty App

    Express trigonometric ratio sin A in terms of cot A.
    Solution
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 77
    CBSEENMA10007865
    Wired Faculty App

    Write the simplest value of
    fraction numerator cos squared straight theta over denominator sinθ end fraction plus sinθ.

    Solution
    space space fraction numerator cos squared straight theta plus sin squared straight theta over denominator sinθ end fraction space equals space 1 over sinθ space equals space cosecθ.
    Question 78
    CBSEENMA10007868
    Wired Faculty App

    Evaluate: fraction numerator 2 space sin squared 63 degree plus 1 plus 2 sin squared 27 degree over denominator 3 cos squared 17 degree minus 2 plus 3 cos squared 73 degree end fraction.
    Solution
    Question 79
    CBSEENMA10007870
    Wired Faculty App

    What is the maximum value of space 1 over secθ ?

    Solution

    The maximum value of <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> is 1.

    Sponsor Area

    Question 80
    CBSEENMA10007871
    Wired Faculty App

    If tanA space equals space 3 over 4 and straight A plus straight B space equals space 90 degree, then what is the value of cot B?
    Solution

    It is given that: tanA space equals space 3 over 4    ...(i)
    and A + B = 90°
    ⇒ A = 90° - B ...(ii)
    Putting the value of (ii) in (i), we get
     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow             cotB space equals space 3 over 4. Ans. 

    Question 81
    CBSEENMA10007872
    Wired Faculty App

    If sin θ = cos θ, find the value of θ.

    Solution

    we have, sin θ = cos θ
    cos (90° -θ) = cos θ
    ⇒ 90° - θ = θ
    ⇒ 2θ = 90°
    ⇒ θ = 45°

    Question 82
    CBSEENMA10007873
    Wired Faculty App

    If tan θ = cot (30° + θ), find the value of θ.

    Solution

    we have, tan θ = cot (30° + θ)
    cot (90°-θ) = cot (30°+ θ)
    ⇒90° - θ = 30° + θ
    2θ = 60°
    ⇒ θ = 30°

    Question 83
    CBSEENMA10007876
    Wired Faculty App

    If sin 3θ = cos (θ - 6°) and θ-6° are acute angles, find the value of θ.

    Solution
    we have, sin 3θ = cos (θ - 6°)
    ⇒ cos (90°-3θ) = cos (θ-6°)
    ⇒90°-3θ = θ-6°
    ⇒84° = 4θ
    ⇒ θ = 21°
    Question 84
    CBSEENMA10007878
    Wired Faculty App

    Given that  <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> what is the value of <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    We have
    tanθ space equals space fraction numerator 1 over denominator square root of 3 end fraction rightwards double arrow space space cot space straight theta space equals space fraction numerator square root of 3 over denominator 1 end fraction
    Now,  
                      space tan squared straight theta plus 1 space equals sec squared straight theta
    rightwards double arrow       <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    rightwards double arrow                1 third plus 1 space equals sec squared straight theta
    rightwards double arrow         sec squared straight theta space equals space 4 over 3
    and     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    space space rightwards double arrow space space space open parentheses fraction numerator square root of 3 over denominator 1 end fraction close parentheses squared plus 1 space equals space cosec squared straight theta space space rightwards double arrow space space space space space space space space space space space 3 plus 1 space equals space cosec squared straight theta space space rightwards double arrow space space space space space space space cosec squared straight theta space equals space 4
    Now, 
              space fraction numerator cosec squared straight theta minus sec squared straight theta over denominator cosec squared straight theta plus sec squared straight theta end fraction
              space space space equals space fraction numerator 4 minus begin display style 4 over 3 end style over denominator 4 plus begin display style 4 over 3 end style end fraction space equals space fraction numerator begin display style fraction numerator 12 minus 4 over denominator 3 end fraction end style over denominator begin display style fraction numerator 12 plus 4 over denominator 3 end fraction end style end fraction space equals space fraction numerator begin display style 8 over 3 end style over denominator begin display style 16 over 3 end style end fraction space equals space 8 over 16 space equals space 1 half.
        
    Question 85
    CBSEENMA10007879
    Wired Faculty App

    If tanθ space equals space 4 over 3 comma what is the value of fraction numerator sinθ plus cosθ over denominator sinθ minus cosθ end fraction ?
    Solution
    Let us draw a right angle triangle, right angled at B.
    We know that
    tan squared straight theta space equals space 4 over 3 equals AB over AC
    Let,AB -4K. BC -3K
    Where K is positive number.
    Using pythagoras theorem, we have
    ⇒ AC2 = AB2 + BC2
    = (4K)2 + (3K)2
    = 16K2 + 9K2
    = 25 K2
    So AC = 5K
    Now, AB = 4K, BC =  3K and AC = 5K
    Therefore,

    fraction numerator sinθ plus cosθ over denominator sinθ minus cosθ end fraction space equals space fraction numerator begin display style AB over AC end style plus begin display style BC over AC end style over denominator begin display style AB over AC end style minus begin display style BC over AC end style end fraction
    equals space fraction numerator begin display style fraction numerator 4 straight K over denominator 5 straight K end fraction end style plus begin display style fraction numerator 3 straight K over denominator 5 straight K end fraction end style over denominator begin display style fraction numerator 4 straight K over denominator 5 straight K end fraction end style minus begin display style fraction numerator 3 straight K over denominator 5 straight K end fraction end style end fraction space equals space fraction numerator begin display style 4 over 5 end style plus begin display style 3 over 5 end style over denominator begin display style 4 over 5 end style minus begin display style 3 over 5 end style end fraction space equals space fraction numerator begin display style fraction numerator 4 plus 3 over denominator 5 end fraction end style over denominator begin display style fraction numerator 4 minus 3 over denominator 5 end fraction end style end fraction space equals space fraction numerator 7 minus 4 over denominator 1 end fraction
    Question 86
    CBSEENMA10007881
    Wired Faculty App

    If space tanA space equals space 5 over 12 comma find the value of (sinA + cosA) secA.
    Solution
    Let us consider a right triangle right angled at B.
    We have,
    rightwards double arrow space space tanA space equals space 5 over 12 space equals space AB over BC
    If AB = 5K,  BC = 12K
    Then,
    space AC squared equals AB squared plus BC squared space equals space left parenthesis 5 straight K right parenthesis squared plus left parenthesis 12 straight K right parenthesis squared space space space space space space space space space space equals space 25 straight K squared plus 144 straight K squared space equals space 169 straight K squared
    So, AC = 13K
    Now,
               sinA space equals space AB over AC equals fraction numerator 5 straight K over denominator 13 straight K end fraction equals 5 over 13 cosA space equals space BC over AC equals fraction numerator 12 straight K over denominator 13 straight K end fraction space equals 12 over 13
    secA space equals space AC over BC equals fraction numerator 13 straight K over denominator 12 straight K end fraction equals 13 over 12
    Therefore,
    left parenthesis sinA plus cosA right parenthesis space secA space equals space open parentheses 5 over 13 plus 12 over 13 close parentheses cross times 13 over 12 equals space open parentheses fraction numerator 5 plus 12 over denominator 13 end fraction close parentheses cross times 13 over 12 space equals space 17 over 13 cross times 13 over 12 space equals space 17 over 12.
    Question 87
    CBSEENMA10007883
    Wired Faculty App

    If cosA space equals space 7 over 25 comma find the value of (tanA + cotA).
    Solution
    Using some figure, we have,
    cosA space equals space 7 over 25 space equals space BC over AC
    Let,  BC = 7K,    AC = 25K
    Then,                
                  space AB squared space equals space AC squared plus BC squared space space space space space space space equals space left parenthesis 25 straight K right parenthesis squared plus left parenthesis 7 straight K right parenthesis squared space space space space space space space equals space 625 straight K squared minus 49 straight K squared space space space space space space space equals space 576 straight K squared space space space space space space space equals 24 straight K squared semicolon space space So space AB space equals space 24 straight K
    Now,          tanA space equals space AB over BC equals fraction numerator 24 straight K over denominator 7 straight K end fraction equals 24 over 7
                       space space cotA space equals space BC over AB space equals space fraction numerator 7 straight K over denominator 24 straight K end fraction equals 7 over 24
    Therefore, tanA plus cotA space equals space 24 over 7 plus 7 over 24 space space space space space space space space space space space space space space space space space space space space space space equals space fraction numerator 576 plus 49 over denominator 168 end fraction space space space space space space space space space space space space space space space space space space space space space equals space 625 over 18
    Question 88
    CBSEENMA10007884
    Wired Faculty App

    If cotθ space equals space 15 over 8 comma then evaluate  "<pre
    Solution
    fraction numerator left parenthesis 2 plus 2 sinθ right parenthesis thin space left parenthesis 1 minus sinθ right parenthesis over denominator left parenthesis 1 plus cosθ right parenthesis thin space left parenthesis 2 minus 2 cosθ right parenthesis end fraction equals space fraction numerator 2 left parenthesis 1 plus sinθ right parenthesis thin space left parenthesis 1 minus sinθ right parenthesis over denominator 2 left parenthesis 1 plus cosθ right parenthesis space left parenthesis 1 minus cosθ right parenthesis end fraction equals space fraction numerator 1 minus sin squared straight theta over denominator 1 minus cos squared straight theta end fraction space equals space fraction numerator cos squared straight theta over denominator sin squared straight theta end fraction space equals space cot squared straight theta equals space open parentheses 15 over 8 close parentheses squared space equals space 225 over 64 space Ans. space
    Question 89
    CBSEENMA10007886
    Wired Faculty App

    If secA space equals space 15 over 7 space and space straight A plus straight B space equals space 90 degree comma space find the value of cosec B.
    Solution
    We have,
              A + B = 90°   rightwards double arrow space space straight A space equals space 90 degree minus straight B       ...(i)
    Now,    secA space equals space 15 over 7
    rightwards double arrow space space space sec left parenthesis 90 degree minus straight B right parenthesis space equals space 15 over 17 space space space space space space space space left square bracket using space left parenthesis straight i right parenthesis right square bracket rightwards double arrow space space space space space space space space space space space space cosecB space equals space 15 over 7 Ans. space
    Question 90
    CBSEENMA10007888
    Wired Faculty App

    Evaluate:
    fraction numerator sec left parenthesis 90 degree minus straight theta right parenthesis times cosecθ space minus space tan left parenthesis 90 degree minus straight theta right parenthesis space cotθ plus left parenthesis cos squared 35 degree plus cos squared 55 degree right parenthesis over denominator tan 5 degree space tan space 15 degree space tan space 45 degree space tan space 75 degree space tan space 85 degree end fraction.
    Solution
    fraction numerator cosecθ. space cosecθ space minus space cotθ. cotθ plus open square brackets cos squared left parenthesis 90 degree minus 55 degree right parenthesis plus cos squared 55 degree close square brackets over denominator tan 5 degree. space tan 85 degree space tan 15 degree space tan space 75 degree space tan space 45 degree end fraction
     = fraction numerator cosec squared straight theta minus cot squared straight theta plus open square brackets sin squared 55 degree plus cos squared 55 degree close square brackets over denominator tan space left parenthesis 90 degree minus 85 degree right parenthesis. space tan space 85 degree space tan left parenthesis 90 degree minus space 75 degree right parenthesis space tan space 75 degree end fraction

    = fraction numerator 1 plus 1 over denominator cot space 85 degree. space tan 85 degree space tan left parenthesis 90 degree minus 75 degree right parenthesis space tan space 75 degree end fraction
    = fraction numerator 2 over denominator 1.1 end fraction space equals space 2 over 1 space equals space 2.
    Question 91
    CBSEENMA10007891
    Wired Faculty App

    Evaluate:
    fraction numerator sin space 10 degree over denominator cos space 80 degree end fraction.

    Solution

    Solution not provided.
    Ans. 1

    Question 92
    CBSEENMA10007892
    Wired Faculty App

    Evaluate:
    space fraction numerator tan space 19 degree over denominator cot space 71 degree end fraction

    Solution

    Solution not provided.
    Ans. 1

    Question 93
    CBSEENMA10007894
    Wired Faculty App

    Evaluate:
    fraction numerator sec space 16 degree over denominator cosec space 74 degree end fraction

    Solution

    Solution not provided.
    Ans. 1

    Question 94
    CBSEENMA10007895
    Wired Faculty App

    Evaluate:
    space fraction numerator tan space 42 degree over denominator cot space 48 degree end fraction

    Solution

    Solution not provided.
    Ans. 1

    Question 95
    CBSEENMA10007897
    Wired Faculty App

    Evaluate:
    fraction numerator cos space 38 degree over denominator sin space 52 degree end fraction

    Solution

    Solution not provided.
    Ans. 1

    Question 96
    CBSEENMA10007898
    Wired Faculty App

    Evaluate:
    space space space open parentheses fraction numerator sin space 10 degree over denominator cos space 80 degree end fraction close parentheses squared plus open parentheses fraction numerator cos space 80 degree over denominator sin space 10 degree end fraction close parentheses squared

    Solution

    Solution not provided.
    Ans. 2

    Question 97
    CBSEENMA10007899
    Wired Faculty App

    Evaluate:
    space space fraction numerator sec space 11 degree over denominator cosec space 79 degree end fraction

    Solution

    Solution not provided.
    Ans. 1

    Question 98
    CBSEENMA10007900
    Wired Faculty App

    Evaluate:
    fraction numerator sin space 21 degree over denominator cos space 69 degree end fraction

    Solution

    Solution not provided.
    Ans. 1

    Question 99
    CBSEENMA10007901
    Wired Faculty App

    Evaluate:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution

    Solution not provided.
    Ans. 1/2

    Question 100
    CBSEENMA10007902
    Wired Faculty App

    Evaluate:
    open parentheses fraction numerator sin space 27 degree over denominator cos space 63 degree end fraction close parentheses squared space minus space open parentheses fraction numerator cos space 63 degree over denominator sin space 27 degree end fraction close parentheses squared

    Solution

    Solution not provided.
    Ans. 0

    Question 101
    CBSEENMA10007903
    Wired Faculty App

    If sin 3θ = cos (θ - 6°), where 3θ and (θ - 6°)  are acute angles. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 24°

    Question 102
    CBSEENMA10007905
    Wired Faculty App

    If sin (θ +24°) = cos θ, where θ and (θ + 24°) is an acute angle. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 33°

    Question 103
    CBSEENMA10007906
    Wired Faculty App

    If cos (2θ + 54°) = sin 4θ, where (2θ + 54°) and 4θ is an acute angle. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 12°

    Question 104
    CBSEENMA10007908
    Wired Faculty App

    If cos 2θ = sin θ, where 2θ and 4θ are acute angles. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 15°

    Question 105
    CBSEENMA10007909
    Wired Faculty App

    If sin 4θ = cos (θ - 10°), where 4θ and (θ -10°) are acute angles. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 20°

    Question 106
    CBSEENMA10007910
    Wired Faculty App

    If sin θ = cos (θ - 45°), where θ and (θ - 45°) are acute angles. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 671/2° 

    Question 107
    CBSEENMA10007911
    Wired Faculty App

    If tan 2θ - cot (θ + 6°), where 2θ and θ + 6° are acute angles. Find the value of θ.

    Solution

    Solution not provided.
    Ans.  28°

    Question 108
    CBSEENMA10007912
    Wired Faculty App

    If sin 5θ = cos 4θ, where 5θ and 4θ are acute angles. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 10°

    Question 109
    CBSEENMA10007913
    Wired Faculty App

    If tan 5θ = cot 4θ, where 5θ and 4θ are acute angles. Find the value of θ.

    Solution

    Solution not provided.
    Ans. 10°

    Question 110
    CBSEENMA10007915
    Wired Faculty App

    Express the following in terms of trigonometric ratios of angles lying between 0° and 45°
    cosec 54° + sin 72° 

    Solution

    Solution not provided.
    Ans. sec 36° + cos 18°

    Question 111
    CBSEENMA10007916
    Wired Faculty App

    Express the following in terms of trigonometric ratios of angles lying between 0° and 45°
    sin 89° + tan 89°

    Solution

    Solution not provided.
    Ans. cos 1° + cot 1°

    Question 112
    CBSEENMA10007917
    Wired Faculty App

    Express the following in terms of trigonometric ratios of angles lying between 0° and 45°
    cosec 69° + cot 69°

    Solution

    Solution not provided.
    Ans. sec 21° + tan 21°

    Question 113
    CBSEENMA10007918
    Wired Faculty App

    Express the following in terms of trigonometric ratios of angles lying between 0° and 45°
    cos 75° + cot 75°

    Solution

    Solution not provided.
    Ans. sin 15° + tan 15°

    Question 114
    CBSEENMA10007920
    Wired Faculty App

    Express the following in terms of trigonometric ratios of angles lying between 0° and 45°
    cos 70° + cot 70°

    Solution

    Solution not provided.
    Ans. sin 20° + tan 20°.

    Question 115
    CBSEENMA10007923
    Wired Faculty App

    In ΔABC, right angled at c,if <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> find the value of sinA. cosB + cosA. sinB

    Solution
    Let us consider a triangle ABC, right angled at C. we have,
    tanA space equals space fraction numerator 1 over denominator square root of 3 end fraction equals BC over AC ref space BC space equals space straight K comma space AC space equals space square root of 3 straight K end root
    then,
           AB squared equals AC squared plus BC squared space equals space left parenthesis square root of 3 straight K right parenthesis squared plus left parenthesis straight K right parenthesis squared equals space 3 straight K squared plus straight K squared space space space space space space space equals space 4 straight K squared space equals space 2 straight K

    Now, 
    sinA space equals space BC over AB equals fraction numerator straight K over denominator 2 straight K end fraction equals 1 cosB space equals space BC over AB equals fraction numerator straight K over denominator 2 straight K end fraction equals 1 half cosA space equals space AC over AB equals fraction numerator square root of 3 straight K over denominator 2 straight K end fraction equals fraction numerator square root of 3 over denominator 2 end fraction comma sinB space equals space AC over AB equals fraction numerator square root of 3 straight K over denominator 2 straight K end fraction equals fraction numerator square root of 3 over denominator 2 end fraction
    Therefore,
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 116
    CBSEENMA10007926
    Wired Faculty App

    If ∠ZB and ∠Q are acute angles such that sin B = sin Q, then prove that ∠B = ∠Q.

    Solution
    Let us consider two right angle triangles right angled at C and R respectively.
    sinB space equals space AC over AB
    Now,
      
    and     <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
       But sin space straight B space equals space sin space straight Q space left parenthesis given right parenthesis
    ∴        AC over AB equals PR over PQ
    rightwards double arrow space space space space space space space space AC over PR equals AB over PQ
    Let      <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>        ...(i)
    In ΔABC,
    Using Pythagoras theorem, we have
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    In increment PQR comma
    Using Pythagoras theorem, we have
                          QR space equals space square root of PQ squared minus PR squared end root
    So,           BC over QR equals fraction numerator straight K square root of PQ squared minus PR squared end root over denominator square root of PQ squared minus PR squared end root end fraction equals straight K space space space... left parenthesis ii right parenthesis
    Comparing (i) and (ii), we get
                     AC over PR equals AB over PQ equals BC over QR
    So, by using SSS similar condition
    ∴          space space increment ACB space tilde space increment PRQ
                    angle straight B space equals space angle straight Q.
       
    Question 117
    CBSEENMA10007930
    Wired Faculty App

    In ΔABC right angled at A, given ∠B = 30°, AC = 3 cm. Find AB, BC and ∠ACB.

    Solution
    Given: ∠B = 30°, ∠A = 90° and AC = 3 cm

     In increment ABC comma
         angle straight A plus angle straight B plus angle straight C space equals space 180 degree
    rightwards double arrow space space space 90 degree plus 30 degree plus angle straight C space equals space 180 degree rightwards double arrow space space space space 120 degree space plus space angle straight C space equals space 180 degree rightwards double arrow space space space space space space space space space space space space space space space space space space angle straight C space equals space 60 degree
    Now,    space space tan space 30 degree space equals space AC over AB
    rightwards double arrow         fraction numerator 1 over denominator square root of 3 end fraction equals 3 over AB
    rightwards double arrow           AB space equals space 3 square root of 3 space cm
    and sin space 30 degree space equals space AC over BC
    rightwards double arrow space space space space space space space space space space space 1 half space equals space 3 over BC rightwards double arrow space space space space space space space space space space space BC space equals space 6 space cm space Hence comma space space space space space angle straight C space equals space 60 degree comma space space AB space equals space 3 square root of 3 space cm comma and space space space space space space space space space space space space space BC space equals space 6 space cm.

    Question 118
    CBSEENMA10007931
    Wired Faculty App

    Find the value of sin 30° geometrically. 

    Solution

    Consider an equilateral ΔABC.
    Since each angle in a equilateral A is 60°.
    ∴ ∠A = ∠B = ∠C = 60°
    Draw a perpendicular from A on side BC.
    Now, ΔABD= ΔACD => BD = DC
    and ΔBAD = ΔCAD [C.P.C.T.]

    Let AB = 2a. Then, BD space equals space 1 half BC space equals space straight a
    In right ΔADB, by Pythagoras theorem.
    AD squared plus BD squared space equals space AB squared space space rightwards double arrow space space AD squared space equals space AB squared minus BD squared space equals space left parenthesis 2 straight a right parenthesis squared minus straight a squared space equals 3 straight a squared space rightwards double arrow space space space AD squared space equals space 3 straight a squared space rightwards double arrow space space AD space equals space straight a square root of 3
    Now, in right ΔADB,
    sin space 30 degree space equals space BD over AB equals fraction numerator straight a over denominator 2 straight a end fraction equals 1 half.

    Question 119
    CBSEENMA10007935
    Wired Faculty App

    Find the value of tan 60°, geometrically.

    Solution
    Consider an equilateral ΔABC. Since each angle in en equilateral triangle is 60°.

    ∴    angle straight A space equals space angle straight B space equals space LC space equals space 60 degree
    Draw a perpendicular AD from A to BC
    Now in space increment ABD space and space increment ACD
                          space angle ADB space equals space angle ADC          [Each = 90 degree]
                           angle ABD space equals space angle ACD           [Each = <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>]
                             AD = AD                              [Common]
    ∴            <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>    [AAS congruency]
    ∴                   BD = DC       [C.P.C.T.]
    Let             AB space equals space 2 straight a space rightwards double arrow space BC space equals space 2 straight a
    Then,     BD space equals space 1 half BC space equals space straight a
    and             <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
            rightwards double arrow         space space AD space equals space straight a square root of 3
      Now, in right increment ADB comma
             tan space 60 degree space equals space AD over BD equals fraction numerator straight a square root of 3 over denominator straight a end fraction equals square root of 3.

    Sponsor Area

    Question 120
    CBSEENMA10007937
    Wired Faculty App

    If sin thin space left parenthesis straight A minus straight B right parenthesis space equals space 1 half comma space space space space space cos space left parenthesis straight A plus straight B right parenthesis space equals space 1 half comma space space space 0 degree less than straight A plus straight B less or equal than 90 degree comma space space straight A greater than straight B. Find A and B.
    Solution

    sin (A-B) = 1 half
    rightwards double arrow          straight A minus straight B space equals space 30 degree             ...(i)
          cos left parenthesis straight A plus straight B right parenthesis space equals space 1 half
    rightwards double arrow           <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>            ...(ii)   
    Solving (i) and (ii), we get
                         straight A equals 45 degree space and space straight B space equals space 15 degree.

    Question 121
    CBSEENMA10007938
    Wired Faculty App

    Evaluate:
    sin 60°. cos 30° - cos 60°. sin 30°.

    Solution
    sin 60°. cos 30° - cos 60°. sin 30°
    space equals space fraction numerator square root of 3 over denominator 2 end fraction cross times fraction numerator square root of 3 over denominator 2 end fraction minus 1 half cross times 1 half space equals space 3 over 4 minus 1 fourth space equals 2 over 4 equals 1 half.
    Question 122
    CBSEENMA10007939
    Wired Faculty App

    Evaluate:
    cos 30°. cos 45° - sin 30°. sin 45°

    Solution
    cos 30°. cos 45° - sin 30°. sin 45°
                           = fraction numerator square root of 3 over denominator 2 end fraction cross times fraction numerator 1 over denominator square root of 2 end fraction minus 1 half cross times fraction numerator 1 over denominator square root of 2 end fraction equals space fraction numerator square root of 3 over denominator 2 square root of 2 end fraction minus fraction numerator 1 over denominator 2 square root of 2 end fraction space equals space fraction numerator square root of 3 minus 1 over denominator 2 square root of 2 end fraction cross times fraction numerator square root of 2 over denominator square root of 2 end fraction equals space fraction numerator square root of 6 minus square root of 2 over denominator 4 end fraction.
    Question 123
    CBSEENMA10007940
    Wired Faculty App

    Evaluate:
    tan2 30° + tan2 45° + cos2 60°

    Solution

    tan2 30° + tan2 45° + cos2 60°
      equals space open parentheses fraction numerator 1 over denominator square root of 3 end fraction close parentheses squared plus left parenthesis 1 right parenthesis squared plus open parentheses 1 half close parentheses squared space equals space 1 third plus 1 plus 1 fourth equals space fraction numerator 4 plus 12 plus 3 over denominator 12 end fraction equals 19 over 12.

    Question 124
    CBSEENMA10007941
    Wired Faculty App

    Evaluate:
    cos 60°. cos 30° - sin 60°. sin 30°.

    Solution

    cos 60°. cos 30° - sin 60°. sin 30°.
     = 1 half cross times fraction numerator square root of 3 over denominator 2 end fraction minus fraction numerator square root of 3 over denominator 2 end fraction cross times 1 half equals fraction numerator square root of 3 over denominator 4 end fraction minus fraction numerator square root of 3 over denominator 4 end fraction equals 0.

    Question 125
    CBSEENMA10007944
    Wired Faculty App

    Evaluate:
    cos 45°.cos 30° + sin 45°. sin 30°

    Solution
    cos 45°.cos 30° + sin 45°. sin 30°
    equals space fraction numerator 1 over denominator square root of 2 end fraction cross times fraction numerator square root of 3 over denominator 2 end fraction plus fraction numerator 1 over denominator square root of 2 end fraction cross times 1 half equals fraction numerator square root of 3 over denominator 2 square root of 2 end fraction plus fraction numerator 1 over denominator 2 square root of 2 end fraction equals space fraction numerator square root of 3 plus 1 over denominator 2 square root of 2 end fraction cross times fraction numerator square root of 2 over denominator square root of 2 end fraction space equals space fraction numerator square root of 2 left parenthesis square root of 3 plus 1 right parenthesis over denominator 4 end fraction space equals space fraction numerator square root of 6 plus square root of 2 over denominator 4 end fraction.
    Question 126
    CBSEENMA10007956
    Wired Faculty App

    Evaluate:
    sin2 30° + 2 cos2 60° + tan2 45°

    Solution

    sin2 30° + 2 cos2 60° + tan2 45°
    space equals space open parentheses 1 half close parentheses squared plus 2 open parentheses 1 half close parentheses squared plus left parenthesis 1 right parenthesis squared space equals space 1 fourth plus 2 cross times 1 fourth plus 1 space equals space 1 fourth plus 1 half plus 1 space equals space fraction numerator 1 plus 2 plus 4 over denominator 4 end fraction equals 7 over 4.

    Question 127
    CBSEENMA10007958
    Wired Faculty App

    Evaluate:
    fraction numerator sin space 30 degree over denominator cos space 45 degree end fraction plus fraction numerator tan squared 45 degree over denominator sec space 60 degree end fraction minus fraction numerator sin space 60 degree over denominator cot space 45 degree end fraction minus fraction numerator cos space 30 degree over denominator sin space 90 degree end fraction
    Solution
    fraction numerator sin space 30 degree over denominator cos space 45 degree end fraction plus fraction numerator tan squared 45 degree over denominator sec space 60 degree end fraction minus fraction numerator sin space 60 degree over denominator cot space 45 degree end fraction minus fraction numerator cos space 30 degree over denominator sin space 90 degree end fraction
    equals space fraction numerator begin display style 1 half end style over denominator begin display style fraction numerator 1 over denominator square root of 2 end fraction end style end fraction plus fraction numerator left parenthesis 1 right parenthesis squared over denominator 2 end fraction minus fraction numerator begin display style fraction numerator square root of 3 over denominator 2 end fraction end style over denominator 1 end fraction minus fraction numerator begin display style fraction numerator square root of 3 over denominator 2 end fraction end style over denominator 1 end fraction space equals space fraction numerator square root of 2 over denominator 2 end fraction plus 1 half minus fraction numerator square root of 3 over denominator 2 end fraction minus fraction numerator square root of 3 over denominator 2 end fraction equals space fraction numerator square root of 2 plus 1 minus square root of 3 minus square root of 3 over denominator 2 end fraction space equals space fraction numerator square root of 2 plus 1 minus 2 square root of 3 over denominator 2 end fraction.
    Question 129
    CBSEENMA10007960
    Wired Faculty App

    Evaluate:
    space space space space space space fraction numerator sin space 15 degree. space cot space 75 degree space plus space cos space 15 degree. space sin space 75 degree over denominator tan space 5 degree. space tan space 30 degree. space tan space 35 degree space tan 55 degree. space tan space 85 degree end fraction
    Solution
    fraction numerator sin space 15 degree. space cos space 75 degree space plus space cos space 15 degree. space sin space 75 degree over denominator tan space 5 degree. space tan space 30 degree. space tan space 35 degree. space tan space 55 degree. space tan space 85 degree end fraction
    equals space fraction numerator sin space 15 degree. space cos left parenthesis 90 degree minus 15 degree right parenthesis space plus space cos space 15 degree. space sin left parenthesis 90 degree minus 15 degree right parenthesis over denominator begin display style fraction numerator 1 over denominator square root of 3 end fraction end style. tan space 5 degree. space tan space 35 degree. space tan space left parenthesis 90 degree minus 35 degree right parenthesis. space tan space left parenthesis 90 degree minus 5 degree right parenthesis end fraction
    equals space fraction numerator sin space 15 degree. space sin space 15 degree space plus space cos space 15 degree. space cos space 15 degree over denominator begin display style fraction numerator 1 over denominator square root of 3 end fraction end style. space tan space 5 degree. space tan space 35 degree. space cot space 35 degree. space cot space 5 degree end fraction equals space fraction numerator square root of 3 left parenthesis sin squared 15 degree plus cos squared 15 degree right parenthesis over denominator open parentheses tan space 5 degree. space begin display style fraction numerator 1 over denominator tan space 5 degree end fraction end style close parentheses space left parenthesis tan space 35 degree. space tan space 35 degree right parenthesis end fraction equals space fraction numerator square root of 3 cross times 1 over denominator 1 cross times 1 end fraction space equals space square root of 3
    Question 130
    CBSEENMA10007961
    Wired Faculty App

    Evaluate without using trigonometric tables
    space tan space 7 degree. space tan space 23 degree. space tan space 60 degree. space tan space 67 degree. space tan space 83 degree space plus space fraction numerator cot space 54 degree over denominator tan space 36 degree end fraction plus sin space 20 degree. space sec space 70 degree space minus space 2.

    Solution
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    equals space tan space 7 degree space. space tan space 83 degree space. space tan space 23 degree. space tan space 67 degree. space tan space 60 degree plus fraction numerator cot space 54 degree over denominator tan space 36 degree end fraction plus sin space 20 degree. space sec space 70 degree space minus 2 equals space tan space left parenthesis 90 degree space minus 83 degree right parenthesis. space tan space 83 degree. space space tan space left parenthesis 90 degree minus 67 degree right parenthesis. space tan space 67 degree. space tan space 60 degree space plus space fraction numerator cot left parenthesis 90 degree minus 36 degree right parenthesis over denominator tan space 36 degree end fraction plus space sin space 20 degree. space sec space left parenthesis 90 degree minus 20 degree right parenthesis minus 2
    space space space equals space cot space 83 degree. space tan space 83 degree. space cot space 67 degree. space tan space 67 degree. space tan space 60 degree space plus space fraction numerator tan space 36 degree over denominator tan space 36 degree end fraction plus sin space 20 degree. space cosec space 20 degree space minus 2 space space space equals space 1 cross times 1 cross times square root of 3 plus 1 plus 1 minus 2 space equals space square root of 3 space Ans. space
    Question 131
    CBSEENMA10007962
    Wired Faculty App

    Evaluate without using trigonometric tables:
    fraction numerator 3 space cos space 55 degree over denominator 7 space sin space 35 degree end fraction minus fraction numerator 4 left parenthesis cos space 70 degree. space cosec space 20 degree right parenthesis over denominator 7 left parenthesis tan space 5 degree. space tan space 25 degree. space tan space 45 degree. space space tan space 65 degree. space tan space 85 degree right parenthesis end fraction.

    Solution
    fraction numerator 3 space cos space 55 degree over denominator 7 space sin space space 35 degree end fractionspace minus space fraction numerator 4 left parenthesis cos space 70 degree. space cosec space 20 degree right parenthesis over denominator 7 left parenthesis tan space 5 degree. space tan space 25 degree. space tan space 45 degree. space tan space 65 degree. space tan space 85 degree right parenthesis end fraction
    fraction numerator 3 space cos space left parenthesis 90 degree space minus 35 degree right parenthesis over denominator 7 space sin space 35 degree end fraction minus fraction numerator 4 left square bracket cos space left parenthesis 90 degree minus 20 degree right parenthesis. space cosec space 20 degree right square bracket over denominator 7 left square bracket tan space left parenthesis 90 degree minus 85 degree right parenthesis. space tan space 85 degree. space tan space left parenthesis 90 degree minus 65 degree right parenthesis. space tan space 65 degree. space tan space 45 degree end fraction.

    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

     
    Question 132
    CBSEENMA10007963
    Wired Faculty App

    Evaluate:
    space 2 over 3 cosec squared 58 degree space minus space 2 over 3 space cot space 58 degree space tan space 32 degree space minus space 5 over 3 space tan space 13 degree. space tan space 37 degree. space tan space 45 degree. space tan space 53 degree. space tan 77 degree.
    Solution
    2 over 3 cosec squared 58 degree minus 2 over 3 space cot space 58 degree space tan 32 degree space minus space 5 over 3 tan 13 degree. tan 37 degree. tan 45 degree. tan space 53 degree. space tan 77 degree
    space space equals space 2 over 3 cosec squared 58 degree space minus space 2 over 3 space cot space 58 degree. space tan left parenthesis 90 degree minus 58 degree right parenthesis minus 5 over 3 left parenthesis space tan space 13 degree. space tan space 77 degree right parenthesis space left parenthesis tan space 37 degree. space tan space 53 degree right parenthesis.
    equals space 2 over 3 cosec squared 58 degree space minus space 2 over 3. space cot squared 58 degree space minus space 5 over 3 left square bracket tan space 13 degree. space tan left parenthesis 90 degree minus 13 degree right parenthesis right square bracket space left square bracket tan space 37 degree. space tan left parenthesis 90 degree minus 37 degree right parenthesis right square bracket space space space space equals space 2 over 3 left parenthesis cosec squared 58 degree space minus space cot squared 58 degree right parenthesis space minus space 5 over 3 space space space space space space space space space space space space space space space space space space space space space space space left square bracket left parenthesis tan space 13 degree. space cot space 13 degree right parenthesis space left parenthesis tan space 37 degree. space cot space 37 degree right parenthesis right square bracket space equals space 2 over 3 cross times 1 minus 5 over 3 left square bracket 1 cross times 1 right square bracket equals space space 2 over 3 minus 5 over 3 space equals space fraction numerator 2 minus 5 over denominator 3 end fraction equals negative 3 over 3 equals negative 1 space space Ans. space
    Question 135
    CBSEENMA10007972
    Wired Faculty App

    Evaluate without using trigonometric tables:
    space space 2 open parentheses fraction numerator cos squared 20 degree plus cos squared 70 degree over denominator sin squared 25 degree plus sin squared 65 degree end fraction close parentheses minus tan space 45 degree plus space tan space 13 degree space tan space 23 degree space tan space 30 degree space tan space 67 degree space tan space 77 degree

    Solution
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre> equals space 2 open square brackets fraction numerator sin space squared space 70 degree plus cos space squared 70 degree over denominator cos squared space 65 degree plus sin squared space 65 degree end fraction close square brackets minus 1 plus tan left parenthesis 90 degree minus 77 degree right parenthesis. space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space tan space 77 degree space. space tan space left parenthesis 90 degree minus 67 degree right parenthesis. space tan space space 67 degree space. space fraction numerator 1 over denominator square root of 3 end fraction
    equals space 2 open parentheses 1 over 1 close parentheses minus 1 plus cot space 77 degree. space tan space 77 degree space. space cot space 67 degree space. space tan space 67 degree space fraction numerator 1 over denominator square root of 3 end fraction equals space 2 minus 1 plus 1.1. space fraction numerator 1 over denominator square root of 3 end fraction equals 2 minus 1 plus fraction numerator 1 over denominator square root of 3 end fraction equals space 1 plus fraction numerator 1 over denominator square root of 3 end fraction space equals space fraction numerator square root of 3 plus 1 over denominator square root of 3 end fraction
    Question 136
    CBSEENMA10007973
    Wired Faculty App

    Without using the trigonometric tables, evaluate the following:
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    fraction numerator sin left parenthesis 90 degree minus 72 degree right parenthesis over denominator cos 72 degree end fraction plus square root of 3 space left square bracket space tan left parenthesis 90 degree minus 80 degree right parenthesis space cross times space tan space 80 degree space cross times space tan left parenthesis 90 degree space minus 50 degree right parenthesis space cross times space tan space 50 degree space cross times space tan space 30 degree right square bracket
                             equals fraction numerator cos space 72 degree over denominator cos space 72 degree end fraction plus square root of 3
    left parenthesis cot space 80 degree space cross times space tan space 80 degree space cross times space cot space 50 degree plus space tan space 50 degree space cross times space fraction numerator 1 over denominator square root of 3 end fraction right parenthesis space equals space 1 plus square root of 3 left parenthesis 1 cross times fraction numerator 1 over denominator square root of 3 end fraction right parenthesis equals space 1 plus fraction numerator square root of 3 over denominator square root of 3 end fraction space equals space 1 plus 1 space equals space 2
    Question 137
    CBSEENMA10007975
    Wired Faculty App

    Without using trigonometric tables, evaluate.
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Solution
    fraction numerator cos space 58 degree over denominator sin space 32 degree end fraction plus fraction numerator sin space 22 degree over denominator cos space 68 degree end fraction minus fraction numerator cos space 38 degree. space cosec space 52 degree over denominator tan space 18 degree. space tan space 35 degree. space tan 60 degree. space tan 72 degree. space tan 55 degree end fraction
    equals space fraction numerator cos space left parenthesis 90 degree space minus 32 degree right parenthesis over denominator sin space 32 degree end fraction plus fraction numerator sin space 22 degree over denominator cos space left parenthesis 90 degree minus 22 degree right parenthesis end fraction minus fraction numerator cos space 38 degree. space cosec space left parenthesis 90 degree minus 38 degree right parenthesis over denominator tan space 18 degree. space tan space 35 degree. space left parenthesis square root of 3 right parenthesis. space tan space left parenthesis 90 degree minus 18 degree right parenthesis. space tan space left parenthesis 90 degree minus 35 degree right parenthesis end fraction space
    space equals space fraction numerator sin space 32 degree over denominator sin space 32 degree end fraction plus fraction numerator sin space 22 degree over denominator sin space 22 degree end fraction minus fraction numerator cos space 38 degree. space sec space 38 degree over denominator square root of 3 left parenthesis tan space 18 degree. space tan space 35 degree. space cot space 18 degree. space cot space 35 degree right parenthesis end fraction
    <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>
    Question 138
    CBSEENMA10007976
    Wired Faculty App

    Express the ratios cos A, tan A, cot A and sec A in terms of sin A.

    Solution

         because space space sin squared straight A space plus space cos squared straight A space equals space 1 rightwards double arrow space space space space space space space space cos squared straight A space equals space 1 minus sin squared straight A rightwards double arrow space space space space space space space space cosA space equals space plus-or-minus square root of 1 minus sin squared straight A end root
    This gives,    cos space straight A space equals space square root of 1 minus sin squared straight A end root
    Hence,      
                    tanA space equals space sinA over cosA equals fraction numerator sinA over denominator square root of 1 minus sin squared straight A end root end fraction cotA space equals space cosA over sinA space equals space fraction numerator square root of 1 minus sin squared straight A end root over denominator sinA end fraction
    and          <pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

    Question 139
    CBSEENMA10007983
    Wired Faculty App

    Prove the following identities:
    secA space left parenthesis 1 minus sinA right parenthesis thin space left parenthesis secA plus tanA right parenthesis space equals 1.

    Solution

    sec A (1 - sin A) (sec A + tan A) = 1
    L.H.S. = sec A (1 - sin A) (sec A + tan A)
                equals space 1 over cosA cross times left parenthesis 1 minus sinA right parenthesis space cross times space open parentheses 1 over cosA plus sinA over cosA close parentheses equals space open parentheses fraction numerator 1 minus sinA over denominator cosA end fraction close parentheses space open parentheses fraction numerator 1 plus sinA over denominator cosA end fraction close parentheses equals space fraction numerator left parenthesis 1 minus sinA right parenthesis thin space left parenthesis 1 plus sinA right parenthesis over denominator cos squared straight A end fraction space equals space fraction numerator 1 minus sin squared straight A over denominator cos squared straight A end fraction equals space fraction numerator cos squared straight A over denominator cos squared straight A end fraction space equals space 1 space equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.

    Question 140
    CBSEENMA10007984
    Wired Faculty App

    Prove the following identities:
    fraction numerator cot space straight A minus cos space straight A over denominator cot space straight A plus cos space straight A end fraction equals fraction numerator cosecA space minus 1 over denominator cosecA plus 1 end fraction.

    Solution
    Question 141
    CBSEENMA10007985
    Wired Faculty App

    Prove the following identities:
    fraction numerator sinθ minus cosθ plus 1 over denominator sinθ plus cosθ minus 1 end fraction space equals space fraction numerator 1 over denominator secθ minus tanθ end fraction.

    Solution
    fraction numerator sinθ minus cosθ plus 1 over denominator sinθ plus cosθ minus 1 end fraction equals fraction numerator 1 over denominator secθ minus tanθ end fraction

    Hence, L.H.S. = R.H.S.
    Question 142
    CBSEENMA10007986
    Wired Faculty App

    Prove the following identities:
    (1 + cot θ- cosec θ) (1 + tan θ+ sec θ) = 2.

    Solution

    (1 + cot θ- cosec θ) (1 + tan θ+ sec θ) = 2.

    Hence, L.H.S. = R.H.S. Proved.

    Question 143
    CBSEENMA10007987
    Wired Faculty App

    If cotA space equals space straight b over straight a comma space prove that:  fraction numerator 2 space secA space plus space 1 over denominator cos space straight A space plus space 2 end fraction equals space fraction numerator square root of straight a squared plus straight b squared end root over denominator straight b end fraction.
    Solution

    Solution not provided.

    Question 144
    CBSEENMA10007988
    Wired Faculty App

    If sinA space equals space straight m over straight n comma space find fraction numerator tanA plus 4 over denominator 4 space cotA space plus 1 end fraction.
    Solution

    Solution not provided.
    Ans. fraction numerator straight m over denominator square root of straight x squared minus straight m squared end root end fraction

    Question 148
    CBSEENMA10007994
    Wired Faculty App

    If tanθ space equals space 4 over 3 comma find the value of fraction numerator 2 space sin space straight theta space minus space 3 space cosθ over denominator 2 space sin space straight theta space plus space 3 space cos space straight theta end fraction.
    Solution

    Solution not provided.
    Ans. fraction numerator negative 1 over denominator 17 end fraction

    Question 149
    CBSEENMA10007995
    Wired Faculty App

    If 16 space cot space straight theta space equals space 12 comma find the value of fraction numerator sinθ plus cosθ over denominator sinθ minus cosθ end fraction.
    Solution

    Solution not provided.
    Ans. 7

    Question 150
    CBSEENMA10007996
    Wired Faculty App

    If cot space straight theta space equals space 12 over 5 comma space show that tan squared straight theta minus sin squared straight theta space equals space sin squared space straight theta. space tan squared straight theta
    Solution

    Solution not provided.

    Question 151
    CBSEENMA10007997
    Wired Faculty App

    If sin space straight A space equals space 1 half comma show that 3 space cosA space minus space 4 space cos cubed straight A space equals space 0.
    Solution

    Solution not provided.

    Question 152
    CBSEENMA10007998
    Wired Faculty App

    If 3 space cot space straight theta space equals space 2 comma find the value of fraction numerator 4 space sin space straight theta space minus space 3 space cos space straight theta over denominator 2 space sin space straight theta space plus space 6 space cos space straight theta end fraction.
    Solution

    Solution not provided.
    Ans.  1 third

    Question 153
    CBSEENMA10008002
    Wired Faculty App

    If tan space straight theta space equals space 4 over 5 comma find the value of fraction numerator 5 space sinθ space minus space 3 space cosθ over denominator 5 space sinθ space plus space 2 space cos space straight theta end fraction.
    Solution

    Solution not provided.
    Ans. 1 over 6

    Question 154
    CBSEENMA10008004
    Wired Faculty App

    If sin space straight theta space equals space fraction numerator square root of 3 over denominator 2 end fraction comma find other trigonometric ratios.
    Solution

    Solution not provided.
    Ans. cosθ space equals space 1 half semicolon space tanθ space equals space fraction numerator square root of 3 over denominator 1 end fraction semicolon space cotθ space equals space fraction numerator 1 over denominator square root of 3 end fraction semicolon space secθ space equals space 2 semicolon space cosecθ space equals space fraction numerator 2 over denominator square root of 3 end fraction

    Question 155
    CBSEENMA10008005
    Wired Faculty App

    If tan space straight theta space equals space square root of 2 minus 1 comma show that sin space straight theta. space cos space straight theta space equals space fraction numerator square root of 2 over denominator 4 end fraction.
    Solution

    Solution not provided.

    Question 156
    CBSEENMA10008006
    Wired Faculty App

    In right-triangle ABC, right angled at B, if cotA space equals space 4 over 3. Show that fraction numerator cos squared straight A minus sin squared straight A over denominator cos space straight A end fraction equals fraction numerator 1 minus tan squared straight A over denominator secA end fraction.

    Solution

    Solution not provided.

    Question 157
    CBSEENMA10008008
    Wired Faculty App

    Consider ΔACB, right-angled at C, in which AC = 4 units, BC = 3 units and ΔABC = θ. Determine the values of:
     left parenthesis straight i right parenthesis space cos squared straight theta plus sin squared straight theta space as space equals space 1 left parenthesis ii right parenthesis space cos squared straight theta space minus space sin squared straight theta space as space equals space fraction numerator negative 7 over denominator 25 end fraction.

    Solution

    Solution not provided.
    Ans. (i) 1,  (ii) fraction numerator negative 7 over denominator 25 end fraction

    Question 161
    CBSEENMA10008015
    Wired Faculty App

    If sin space straight theta space equals space 3 over 4 comma prove that : square root of fraction numerator cosec squared straight theta minus 1 over denominator sec squared straight theta minus 1 end fraction end root space equals space fraction numerator square root of 7 over denominator 3 end fraction.
    Solution

    Solution not provided.

    Question 162
    CBSEENMA10008016
    Wired Faculty App

    Evaluate the following:
    sin 60°. cos 45° + cos 60° sin 45°
    Solution

    Solution not provided.
    Ans. fraction numerator square root of 3 plus 1 over denominator 2 square root of 2 end fraction semicolon

    Question 163
    CBSEENMA10008018
    Wired Faculty App

    Evaluate the following:
    sin 30°. cos 45° + cos 30° sin 45°
    Solution

    Solution not provided.
    Ans.  fraction numerator square root of 3 plus 1 over denominator 2 square root of 2 end fraction semicolon

    Question 164
    CBSEENMA10008020
    Wired Faculty App

    Evaluate the following:
    3 cos2 30° + sec2 30° + 2 cos 0° + 3 sin 90° - tan2 60°
    Solution

    Solution not provided.
    Ans.  67 over 12 semicolon

    Question 165
    CBSEENMA10008021
    Wired Faculty App

    Evaluate the following:
    sin2 60° + sec2 30° + sin 90° + 3 cos 0° - tan2 60°
    Solution

    Solution not provided.
    Ans.  49 over 12 semicolon

    Question 166
    CBSEENMA10008023
    Wired Faculty App

    Evaluate the following:
    fraction numerator 4 space sin space 30 degree space plus space cos squared 45 degree minus 4 cos squared 60 degree over denominator 2 space sin space 30 degree. space cosec space 30 degree plus tan squared 45 degree end fraction.
    Solution

    Solution not provided.
    Ans.  1

    Question 167
    CBSEENMA10008024
    Wired Faculty App

    If cos (A - B) = 1, sin (A + B) = 1. Find A and B.

    Solution

    Solution not provided.
    Ans.  straight A space equals space 45 degree comma space space straight B space equals space 45 degree

    Question 168
    CBSEENMA10008026
    Wired Faculty App

    If tan (A + B) = 1,  tan (A - B) = 1. Find A and B.

    Solution

    Solution not provided.
    Ans.  straight A space equals space 45 degree comma space space straight B space equals space 45 degree

    Question 169
    CBSEENMA10008027
    Wired Faculty App

    If sin left parenthesis straight x minus straight y right parenthesis space equals space 1 half space and space cos left parenthesis straight x plus straight y right parenthesis space equals space 1 half. Find x and y.
    Solution

    Solution not provided.
    Ans.  straight x equals 45 degree comma space straight y space equals space 15 degree.

    Question 170
    CBSEENMA10008029
    Wired Faculty App

    Find the value of x in the following:
     If tan 3.x = sin 45° . cos 45° + sin 30°

    Solution

    Solution not provided.
    Ans.   15 degree

    Question 171
    CBSEENMA10008030
    Wired Faculty App

    Find the value of x in the following:
     If sin 2.x = sin 60° . cos 30° - cos 60° . sin 30°

    Solution

    Solution not provided.
    Ans.   15 degree

    Question 172
    CBSEENMA10008031
    Wired Faculty App

    Find the value of x in the following:
    If cos (40° + x) = sin 30°.

    Solution

    Solution not provided.
    Ans.   20 degree

    Question 173
    CBSEENMA10008033
    Wired Faculty App

     Determine x, if fraction numerator straight x space sin squared 30 degree. space cos squared space 60 degree over denominator 4 space cos to the power of 2 space end exponent 45 degree end fraction space equals space fraction numerator 3 space sin squared 45 degree plus 2 cos squared 30 degree over denominator sin squared 90 degree minus 4 cos squared 45 degree end fraction.

    Solution

    Solution not provided.
    Ans.   -96

    Question 174
    CBSEENMA10008035
    Wired Faculty App

    If sin left parenthesis straight A plus straight B plus straight C right parenthesis equals space 1 comma space space tan space left parenthesis straight A minus straight B right parenthesis space equals space fraction numerator 1 over denominator square root of 3 end fraction space and space sec left parenthesis straight A plus straight C right parenthesis space equals 2 comma find A, B and C when they are acute.
    Solution

    Solution not provided.
    Ans.   angle straight A equals 60 degree semicolon space angle straight B space equals space 30 degree semicolon space angle straight C space equals space 0.

    Question 175
    CBSEENMA10008036
    Wired Faculty App

    If sin left parenthesis straight A plus 2 straight B right parenthesis space equals space fraction numerator square root of 3 over denominator 2 end fraction space and space cos space left parenthesis straight A plus 4 straight B right parenthesis. Find A and B.
    Solution

    Solution not provided.


    Question 177
    CBSEENMA10008038
    Wired Faculty App

    If A = B = 60°, verify that
    cos (A - B) = cos A . cos B + sin A. sin B

    Solution

    Solution not provided.


    Question 178
    CBSEENMA10008039
    Wired Faculty App

    If A = B = 60°, verify that
    sin (A - B) = sin A . cos B - cos A . sin B

    Solution

    Solution not provided.


    Question 179
    CBSEENMA10008040
    Wired Faculty App

    If A = B = 60°, verify that
    tan left parenthesis straight A minus straight B right parenthesis space equals space fraction numerator tanA minus tanB over denominator 1 plus tanA. space tanB end fraction.

    Solution

    Solution not provided.


    Question 180
    CBSEENMA10008041
    Wired Faculty App

    If A = 30° and B = 60°, verify that
    sin (A + B) = sin A . cos B + cos A . sin B

    Solution

    Solution not provided.


    Question 181
    CBSEENMA10008042
    Wired Faculty App

    If A = 30° and B = 60°, verify that
    cos (A + B) = cos A . cos B - sin A . sin B.

    Solution

    Solution not provided.


    Question 182
    CBSEENMA10008043
    Wired Faculty App

    If A and B are acute angles sum that tan space straight A space equals space 1 half comma space tanB space equals space 1 third space and space tan left parenthesis straight A plus straight B right parenthesis space equals space fraction numerator tanA plus tanB over denominator 1 minus tanA. space tanB end fraction comma space find A + B.

    Solution

    Solution not provided.
    Ans. 45 degree


    Question 183
    CBSEENMA10008045
    Wired Faculty App

    If θ = 30°, verify that
    tan space 2 straight theta space equals space fraction numerator 2 space tanθ over denominator 1 minus tan squared straight theta end fraction

    Solution

    Solution not provided.


    Question 184
    CBSEENMA10008046
    Wired Faculty App

    If θ = 30°, verify that
    cos 3θ = 4 cos3θ - 3 cosθ.

    Solution

    Solution not provided.


    Question 185
    CBSEENMA10008047
    Wired Faculty App

    If θ = 30°, verify that
    sin space 2 straight theta space equals space fraction numerator 2 tanθ over denominator 1 minus tan squared straight theta end fraction

    Solution

    Solution not provided.


    Question 186
    CBSEENMA10008048
    Wired Faculty App

    If θ = 30°, verify that
    cos space 2 straight theta space equals space fraction numerator 1 minus tan squared straight theta over denominator 1 plus tan squared straight theta end fraction.

    Solution

    Solution not provided.


    Question 187
    CBSEENMA10008049
    Wired Faculty App

    Evaluate:
    fraction numerator sin space 70 degree over denominator cos space 20 degree end fraction plus fraction numerator cos space 20 degree over denominator sin space 70 degree end fraction minus 2 space cos space 70 degree. space cosec space 20 degree.

    Solution

    Solution not provided.
    Ans. 0


    Question 188
    CBSEENMA10008050
    Wired Faculty App

    Evaluate:
    fraction numerator cos space 70 degree over denominator sin space 20 degree end fraction plus fraction numerator cos space 55 degree cross times cosec space 35 degree over denominator tan space 5 degree cross times tan space 25 degree cross times tan space 45 degree cross times tan space 65 degree cross times tan space 55 degree end fraction

    Solution

    Solution not provided.
    Ans. 2


    Question 189
    CBSEENMA10008051
    Wired Faculty App

    Evaluate:
    2 open parentheses fraction numerator cos squared 20 degree plus cos squared 70 degree over denominator sin squared 25 degree plus sin squared 65 degree end fraction close parentheses minus tan 45 degree plus tan 13 degree. space tan 23 degree. space tan space 30 degree. space tan space 67 degree comma space tan 77 degree.

    Solution

    Solution not provided.
    Ans. fraction numerator square root of 3 plus 1 over denominator square root of 3 end fraction


    Question 190
    CBSEENMA10008053
    Wired Faculty App

    Evaluate:
    fraction numerator cos space 70 degree over denominator sin space 20 degree end fraction plus fraction numerator cos space 59 degree over denominator sin space 31 degree end fraction minus 8 space sin squared 30.

    Solution

    Solution not provided.
    Ans. 0


    Question 191
    CBSEENMA10008054
    Wired Faculty App

    Evaluate:
    fraction numerator cos space 70 degree over denominator sin space 20 degree end fraction plus fraction numerator cos space 55 degree. space cosec space 35 degree over denominator tan space 65 degree. space tan space 25 degree end fraction minus tan space 45 degree. space tan space 5 degree. space tan space 85 degree.

    Solution

    Solution not provided.
    Ans. 1


    Question 192
    CBSEENMA10008055
    Wired Faculty App

    Evaluate:
    fraction numerator 2 space sin space 68 degree over denominator cos space 22 degree end fraction minus fraction numerator 2 space cot space 15 degree over denominator 5 space tan space 75 degree end fraction minus fraction numerator 3 space tan space 45 degree. space tan space 20 degree. space tan space 40 degree. space tan space 50 degree. space tan space 70 degree over denominator 5 end fraction

    Solution

    Solution not provided.
    Ans. 1


    Question 193
    CBSEENMA10008056
    Wired Faculty App

    Show that:
    tan 20°. tan 35°. tan 45°. tan 55° tan 70° = 1
    Solution

    Solution not provided.



    Question 194
    CBSEENMA10008057
    Wired Faculty App

    Show that:
    sin 63°. cos 27° + cos 63°. sin 27° = 1
    Solution

    Solution not provided.



    Question 195
    CBSEENMA10008058
    Wired Faculty App

    Show that:
    sin 63°. cos 27° + cos 63°. sin 27° = 1
    Solution
    Solution not provided.
    Question 196
    CBSEENMA10008059
    Wired Faculty App

    Show that:
    sin 20°. tan 70°. tan 60°. sec 70°. tan 20° = square root of 3.
    Solution
    Solution not provided.
    Question 197
    CBSEENMA10008060
    Wired Faculty App

    Show that:
    cos 38°. cos 52° - sin 38°. sin 52° = 0
    Solution
    Solution not provided.
    Question 198
    CBSEENMA10008061
    Wired Faculty App

    Show that:
    tan 48°. tan 23°. tan 42°. tan 67° = 1.
    Solution
    Solution not provided.
    Question 202
    CBSEENMA10008065
    Wired Faculty App

    If A, B, C are interior angles of a triangle ABC, prove that tan open parentheses fraction numerator straight B plus straight C over denominator 2 end fraction close parentheses equals space space cot straight A over 2.

    Solution
    Solution not provided.

    Question 203
    CBSEENMA10008066
    Wired Faculty App

    If A, B, C are interior angles of a triangle ABC. Prove that cot open parentheses fraction numerator straight B plus straight C over denominator 2 end fraction close parentheses equals space space tan straight A over 2.

    Solution
    Solution not provided.

    Question 204
    CBSEENMA10008068
    Wired Faculty App

    If A, B, C are interior angles of a triangle ABC. Prove that cos open parentheses fraction numerator straight A plus straight C over denominator 2 end fraction close parentheses space equals space sin straight B over 2.

    Solution
    Solution not provided.

    Question 205
    CBSEENMA10008069
    Wired Faculty App

    If A, B, C are interior angles of a increment ABC Prove that sec open parentheses fraction numerator straight A plus straight B over denominator 2 end fraction close parentheses space equals space cosec straight C over 2.

    Solution
    Solution not provided.

    Question 206
    CBSEENMA10008070
    Wired Faculty App

    If A, B, C are interior angles of a ΔABC, show that
    (i)   sin space fraction numerator straight B plus straight C over denominator 2 end fraction equals space cos straight A over 2.
    (ii)   cos fraction numerator straight B plus straight C over denominator 2 end fraction equals sin straight A over 2.

    Solution
    Solution not provided.

    Question 207
    CBSEENMA10008072
    Wired Faculty App

    If A, B, C are interior angles of a ΔABC, show that
    (i)   cos squared straight A over 2 plus cos squared open parentheses fraction numerator straight B plus straight C over denominator 2 end fraction close parentheses equals 1.
    (ii) 1 plus tan squared open parentheses fraction numerator straight B plus straight C over denominator 2 end fraction close parentheses space equals space cosec squared straight A.

    Solution
    Solution not provided.

    Question 209
    CBSEENMA10008075
    Wired Faculty App

    Prove the following identities:
    tan θ + cot θ = sec θ. cosec θ

    Solution
    Solution not provided.

    Question 210
    CBSEENMA10008076
    Wired Faculty App

    Prove the following identities:
    fraction numerator tanθ plus sinθ over denominator tanθ minus sinθ end fraction equals fraction numerator secθ plus 1 over denominator secθ minus 1 end fraction

    Solution
    Solution not provided.

    Question 211
    CBSEENMA10008077
    Wired Faculty App

    Prove the following identities:
    fraction numerator cosθ over denominator cosecθ plus 1 end fraction plus fraction numerator cosθ over denominator cosecθ minus 1 end fraction equals space space 2 tanθ

    Solution
    Solution not provided.

    Question 212
    CBSEENMA10008079
    Wired Faculty App

    Prove the following identities:
    fraction numerator left parenthesis 1 minus sinθ right parenthesis squared plus left parenthesis 1 minus sinθ right parenthesis squared over denominator 2 space cos squared straight theta end fraction space equals space fraction numerator 1 plus sin squared straight theta over denominator 1 minus sin squared straight theta end fraction.

    Solution
    Solution not provided.

    Question 213
    CBSEENMA10008087
    Wired Faculty App

    Prove the following identities:
    square root of fraction numerator 1 plus sinθ over denominator 1 minus sinθ end fraction end root space equals space secθ plus tanθ

    Solution
    Solution not provided.

    Question 214
    CBSEENMA10008088
    Wired Faculty App

    Prove the following identities:
    square root of fraction numerator 1 plus cosβ over denominator 1 minus cosβ end fraction end root space equals space cosecβ plus cotβ

    Solution
    Solution not provided.

    Question 215
    CBSEENMA10008089
    Wired Faculty App

    Prove the following identities:
    square root of fraction numerator 1 minus sinθ over denominator 1 plus sinθ end fraction end root equals space space secθ plus tanθ

    Solution
    Solution not provided.

    Question 216
    CBSEENMA10008092
    Wired Faculty App

    Prove the following identities:
    square root of fraction numerator secθ minus 1 over denominator secθ plus 1 end fraction end root plus square root of fraction numerator secθ plus 1 over denominator secθ minus 1 end fraction end root space equals space 2 space cosecθ

    Solution
    Solution not provided.

    Question 217
    CBSEENMA10008093
    Wired Faculty App

    Prove the following identities:
    square root of fraction numerator 1 plus cosθ over denominator 1 minus cosθ end fraction end root plus square root of fraction numerator 1 minus cosθ over denominator 1 plus cosθ end fraction end root space equals space 2 space cosec space straight theta

    Solution
    Solution not provided.

    Question 218
    CBSEENMA10008097
    Wired Faculty App

    Prove the following identities:
    fraction numerator tan space straight theta over denominator 1 minus cotθ end fraction plus fraction numerator cot space straight theta over denominator 1 minus tanθ end fraction space equals space 1 plus tanθ plus cotθ space equals space 1 plus secθ. space cosecθ

    Solution
    Solution not provided.

    Question 219
    CBSEENMA10008098
    Wired Faculty App

    Prove the following identities:
    fraction numerator sinθ plus cosθ over denominator sinθ minus cosθ end fraction plus fraction numerator sinθ minus cosθ over denominator sinθ plus cosθ end fraction space equals space fraction numerator 2 over denominator sin squared straight theta plus cos squared straight theta end fraction equals fraction numerator 2 over denominator 2 sin squared straight theta minus 1 end fraction

    Solution
    Solution not provided.

    Question 220
    CBSEENMA10008100
    Wired Faculty App

    Prove the following identities:
    fraction numerator sinA minus sinB over denominator cosA plus cosB end fraction plus fraction numerator cosA minus cosB over denominator sinA plus sinB end fraction equals 0

    Solution
    Solution not provided.

    Question 221
    CBSEENMA10008104
    Wired Faculty App

    Prove the following identities:
    (1 + cot θ - cosec θ) (1 + tan θ + sec) = 2

    Solution
    Solution not provided.

    Question 222
    CBSEENMA10008111
    Wired Faculty App

    Prove the following identities:
    fraction numerator sin space straight theta over denominator cot space straight theta plus cosecθ end fraction space equals space 2 plus fraction numerator sinθ over denominator cotθ minus cosecθ end fraction.

    Solution
    Solution not provided.

    Question 223
    CBSEENMA10008113
    Wired Faculty App

    Prove the following identities:
    sin6 θ + cos6 θ + 3 sin2 θ . cos2 θ = 1

    Solution

    Solution not provided.

    Question 226
    CBSEENMA10008116
    Wired Faculty App

    Prove the following identities:
    cot squared straight A open parentheses fraction numerator secA minus 1 over denominator 1 plus sinA end fraction close parentheses plus sec squared straight A open parentheses fraction numerator sinA minus 1 over denominator 1 plus secA end fraction close parentheses equals 0

    Solution

    Solution not provided.

    Question 227
    CBSEENMA10008117
    Wired Faculty App

    Prove the following identities:
    fraction numerator cosA over denominator 1 minus sinA end fraction plus fraction numerator sinA over denominator 1 minus cosA end fraction plus 1 space equals space fraction numerator sinA. space cosA over denominator left parenthesis 1 minus sinA right parenthesis space left parenthesis 1 minus cosA right parenthesis end fraction.

    Solution

    Solution not provided.

    Question 228
    CBSEENMA10008118
    Wired Faculty App

    Prove the following identities:
    (sin4 θ + cos4 θ) = 1 - 2 sin2 θ . cos2 θ

    Solution

    Solution not provided.

    Question 229
    CBSEENMA10008119
    Wired Faculty App

    Prove the following identities:
    (sin4 θ - sec2 θ) = tan4 θ + tan2 θ

    Solution

    Solution not provided.

    Question 231
    CBSEENMA10008124
    Wired Faculty App

    Prove the following identities:
     fraction numerator cos squared straight theta over denominator 1 minus tanθ end fraction plus fraction numerator sin cubed straight theta over denominator sinθ minus cosθ end fraction equals 1 plus sinθ. space cosθ

    Solution

    Solution not provided.

    Question 233
    CBSEENMA10008126
    Wired Faculty App

    Evaluate:
    sin 63°. cos 27° + cos 63° . sin 27°

    Solution

    Solution not provided.

    Question 234
    CBSEENMA10008127
    Wired Faculty App

    Evaluate:
    fraction numerator sin squared 20 degree plus sin squared 70 degree over denominator cos squared 20 degree plus cos squared 70 degree end fraction plus fraction numerator sin left parenthesis 90 degree minus straight theta right parenthesis. sinθ over denominator tanθ end fraction plus fraction numerator cos left parenthesis 90 degree minus straight theta right parenthesis. space cosθ over denominator cotθ end fraction

    Solution

    Solution not provided.

    Question 235
    CBSEENMA10008128
    Wired Faculty App

    Evaluate:
    cosθ. space sinθ space minus space fraction numerator sinθ. space cos left parenthesis 90 degree minus straight theta right parenthesis. space cosθ over denominator sec left parenthesis 90 degree minus straight theta right parenthesis end fraction minus fraction numerator cosθ. space sin left parenthesis 90 degree minus straight theta right parenthesis. space sinθ over denominator cosec left parenthesis 90 degree minus straight theta right parenthesis end fraction

    Solution

    Solution not provided.

    Question 236
    CBSEENMA10008129
    Wired Faculty App

    Evaluate:
    cos left parenthesis 40 degree plus straight theta right parenthesis space minus space sin left parenthesis 50 degree minus straight theta right parenthesis plus fraction numerator cos squared 40 degree plus cos squared 50 degree over denominator sin squared 40 degree plus sin squared 50 degree end fraction

    Solution

    Solution not provided.

    Question 237
    CBSEENMA10008130
    Wired Faculty App

    Evaluate:
    fraction numerator cos squared 20 degree plus cos squared 70 degree over denominator sin squared 59 degree plus sin squared 31 degree end fraction plus sin space 35 degree. space sec space 55 degree.

    Solution

    Solution not provided.

    Question 238
    CBSEENMA10008131
    Wired Faculty App

    Evaluate:
    sin 47°. cos 43° + cos 47° . sin 43°

    Solution

    Solution not provided.
    Ans. 1

    Question 239
    CBSEENMA10008132
    Wired Faculty App

    Evaluate:
    sin 47° . cos 43° + cos 47° . sin 43°

    Solution

    Solution not provided.
    Ans. -2

    Question 240
    CBSEENMA10008133
    Wired Faculty App

    Evaluate:
    sin 35°.cos 55° + cos 35°. sin 55°

    Solution

    Solution not provided.
    Ans. 1

    Question 241
    CBSEENMA10008134
    Wired Faculty App

    Evaluate:
    sin 63°.cos 27° + cos 63°. sin 27°

    Solution

    Solution not provided.
    Ans. 1

    Question 242
    CBSEENMA10008135
    Wired Faculty App

    Evaluate:
    sin 48° . sec 42° + cos 48° . cosec 42°.

    Solution

    Solution not provided.
    Ans. 2

    Question 243
    CBSEENMA10008136
    Wired Faculty App

    If cos squared straight alpha space minus space sin 2 straight alpha space equals space tan squared straight beta comma then prove that cos space straight beta space equals space fraction numerator 1 over denominator square root of 2 cosα end fraction.
    Solution

    Solution not provided.

    Question 244
    CBSEENMA10008137
    Wired Faculty App

    If cosec θ - sin θ = m3 and sec θ - cos θ = n3 then prove that m4n2 + m2n4 = 1.

    Solution

    Solution not provided.

    Question 245
    CBSEENMA10008138
    Wired Faculty App

    Simplify:
    fraction numerator sin space 73 degree over denominator cos space 17 degree end fraction plus 3 fraction numerator sec space 31 degree over denominator cosec space 59 degree end fraction minus 2 fraction numerator left parenthesis sin squared 41 degree plus sin squared 49 degree right parenthesis over denominator sec squared 20 degree minus cot squared 70 degree plus 3 tan squared 30 degree end fraction.

    Solution

    Solution not provided.
    Ans. 3

    Question 246
    CBSEENMA10008139
    Wired Faculty App

    If cosec θ - sin θ = a, sec θ - cos θ = b. Prove that a2 b2 (a2 + b2 + 3) = 1.

    Solution

    Solution not provided.

    Question 247
    CBSEENMA10008140
    Wired Faculty App

    Show that (sec θ - cosec θ) (1+ tan θ + cot θ) = sec a2.tan θ - cosec θ.cot θ.

    Solution

    Solution not provided.

    Question 248
    CBSEENMA10008141
    Wired Faculty App

    If cosec θ - sin θ = a, sec θ - cos θ = b. Prove that a2 b2 (a2 + b2 + 3) = 1.

    Solution

    Solution not provided.

    Question 249
    CBSEENMA10008142
    Wired Faculty App

    If secθ space equals space straight x plus fraction numerator 1 over denominator 4 straight x end fraction comma Prove that secθ plus tanθ space equals space 2 straight x space or space fraction numerator 1 over denominator 2 straight x end fraction.

    Solution

    Solution not provided.

    Question 250
    CBSEENMA10008143
    Wired Faculty App

    Show that fraction numerator cosec space straight theta space plus space cotθ over denominator cosecθ space minus space cotθ end fraction space equals space 1 plus 2 cot squared straight theta plus 2 cosecθ. space cotθ
    Solution

    Solution not provided.

    Question 251
    CBSEENMA10008144
    Wired Faculty App

    If secθ space equals space straight x plus fraction numerator 1 over denominator 4 straight x end fraction comma prove that secθ plus tanθ space equals space 2 space straight x space or space fraction numerator 1 over denominator 2 straight x end fraction.
    Solution

    Solution not provided.

    Question 252
    CBSEENMA10008145
    Wired Faculty App

    Show that fraction numerator cosecθ plus cotθ over denominator cosecθ minus cotθ end fraction equals 1 plus 2 cot squared straight theta plus 2 cosecθ. space cotθ
    Solution

    Solution not provided.

    Question 254
    CBSEENMA10008147
    Wired Faculty App

    If cosθ plus sinθ space equals space square root of 2 space cosθ comma show that cosθ minus sinθ space equals space square root of 2 space sin space straight theta.
    Solution

    Solution not provided.

    Question 257
    CBSEENMA10008150
    Wired Faculty App

    If sin space straight theta plus space cos space straight theta space equals space square root of 2 space cos left parenthesis 90 degree minus straight theta right parenthesis. Determine cot space straight theta.
    Solution

    Solution not provided.
    Ans. square root of 2 minus 1

    Question 258
    CBSEENMA10008151
    Wired Faculty App

    If tanθ space equals space 1 space space and space sinβ space equals space fraction numerator 1 over denominator square root of 2 end fraction. Find the value of cos (θ + β), if θ and β are both acute angles.
    Solution

    Solution not provided.
    Ans. 0 degree.

    Question 259
    CBSEENMA10008152
    Wired Faculty App

    If fraction numerator cos space straight alpha over denominator cos space straight beta end fraction space equals space straight m space and space fraction numerator cos space straight beta over denominator sin space straight beta end fraction space equals space straight n comma show that left parenthesis straight m squared plus straight n squared right parenthesis space cos squared straight beta space equals space straight n squared.
    Solution

    Solution not provided.

    Question 260
    CBSEENMA10008153
    Wired Faculty App

    If x = a cos θ – b sin θ;   y = a sin θ + b cos θ. Prove that x2+ y2 = a2 + b2

    Solution

    Solution not provided.

    Question 262
    CBSEENMA10008155
    Wired Faculty App

    If tan θ + sin θ = m and tan θ – sin θ = n, show that straight m squared minus straight n squared space equals space 4 square root of mn.

    Solution

    Solution not provided.

    Question 265
    CBSEENMA10008158
    Wired Faculty App

    If straight x over straight a cos space straight theta space plus space straight y over straight b sinθ space equals space 1 and straight x over straight a sinθ space minus space straight y over straight b cosθ space equals space 1 comma Prove that straight x squared over straight a squared plus straight y squared over straight b squared equals 2.
    Solution

    Solution not provided.

    Question 266
    CBSEENMA10008159
    Wired Faculty App

    If straight x equals acos cubed straight theta comma space space straight y equals bsin cubed straight theta comma prove that open parentheses straight x over straight a close parentheses to the power of 2 divided by 3 end exponent plus open parentheses straight y over straight b close parentheses to the power of 2 divided by 3 end exponent space equals space 1.
    Solution

    Solution not provided.

    Question 268
    CBSEENMA10008161
    Wired Faculty App

    If sec θ + tan θ = p show that fraction numerator straight p squared minus 1 over denominator straight p squared plus 1 end fraction space equals space sinθ.

    Solution

    Solution not provided.

    Question 269
    CBSEENMA10008162
    Wired Faculty App

    If tan B + sin B = m and tan B – sin B = n, prove that (m2 – n2)2 = 16 mn.

    Solution

    Solution not provided.

    Question 270
    CBSEENMA10008163
    Wired Faculty App

    If cosθ plus sinθ space equals space square root of 2 space cosθ
    show that cosθ minus sinθ space equals space square root of 2 space sinθ.
    Solution

    Solution not provided.

    Question 272
    CBSEENMA10008165
    Wired Faculty App

    If sin θ + sin2 θ = 1. Prove that cos2 θ + cos2 θ = 1

    Solution

    Solution not provided.

    Question 273
    CBSEENMA10008166
    Wired Faculty App

    If 3 sin θ + 5 cos θ = 5, prove that 5 sin θ – 3 cos θ = ± 3.

    Solution

    Solution not provided.

    Question 274
    CBSEENMA10008167
    Wired Faculty App

    Prove fraction numerator cos cubed straight theta plus sin cubed straight theta over denominator cosθ plus sinθ end fraction plus fraction numerator cos cubed straight theta minus sin cubed straight theta over denominator cosθ minus sinθ end fraction equals 2.
    Solution

    Solution not provided.

    Question 275
    CBSEENMA10008168
    Wired Faculty App

    In the given Fig. ABC is a right angled triangle. D is the mid-point of B. Show that tanθ over tanφ equals 1 half.

    Solution

    Solution not provided.

    Question 276
    CBSEENMA10008169
    Wired Faculty App

    Prove that: fraction numerator sinθ over denominator secθ plus tanθ minus 1 end fraction plus fraction numerator cosθ over denominator cosecθ plus cotθ minus 1 end fraction equals 1.
    Solution

    Solution not provided.

    Question 278
    CBSEENMA10008171
    Wired Faculty App

    Evaluate: tan 35°. tan 40°. tan 45°. tan 50°. tan 55°.

    Solution

    Solution not provided.

    Question 279
    CBSEENMA10008172
    Wired Faculty App

    Show that: open parentheses cosecθ minus sinθ close parentheses space left parenthesis secθ. space cosθ right parenthesis space equals space fraction numerator 1 over denominator tanθ plus cotθ end fraction.

    Solution

    Solution not provided.

    Question 280
    CBSEENMA10008173
    Wired Faculty App

    Show that fraction numerator sinθ minus 2 sin cubed straight theta over denominator 2 space cos cubed straight theta minus cosθ end fraction space equals space tanθ.

    Solution

    Solution not provided.

    Question 281
    CBSEENMA10008174
    Wired Faculty App

    Show that 2 sec2 θ – sec4 θ – 2 cosec2 θ + cosec4θ = cot4 θ – tan4 θ.

    Solution

    Solution not provided.

    Question 282
    CBSEENMA10008175
    Wired Faculty App

    Show that: fraction numerator cosA over denominator 1 minus tanA end fraction plus fraction numerator sinA over denominator 1 minus cotA end fraction equals sinA plus cosA.

    Solution

    Solution not provided.

    Question 283
    CBSEENMA10008176
    Wired Faculty App

    Prove that fraction numerator sin space straight theta over denominator 1 plus cosθ end fraction plus fraction numerator 1 plus cosθ over denominator sinθ end fraction space equals space 2 space cosecθ.
    Solution

    Solution not provided.

    Question 284
    CBSEENMA10008177
    Wired Faculty App

    If 3 tan θ = 4. Find the value of fraction numerator 2 space sin space straight theta space plus space 3 space cos space straight theta over denominator 2 space sin space straight theta space minus space 3 space cos space straight theta end fraction.

    Solution

    Solution not provided.
    Ans. -17

    Question 285
    CBSEENMA10008178
    Wired Faculty App

    Prove that: (sin θ + sec θ)2 + (cos θ + cosec θ)2 = (1 + sec θ. cosec θ)2.

    Solution

    Solution not provided.

    Question 286
    CBSEENMA10008179
    Wired Faculty App

    If 4 tan θ = 3, find the value of fraction numerator 4 space sin space straight theta space minus space 2 space cosθ over denominator 4 space sinθ space plus space 3 space cosθ end fraction.

    Solution

    Solution not provided.
    Ans. 1 over 6

    Question 287
    CBSEENMA10008180
    Wired Faculty App

    Prove that:
    fraction numerator cos squared straight theta over denominator 1 minus tanθ end fraction plus fraction numerator sin cubed straight theta over denominator sin space straight theta space minus space cos space straight theta end fraction space equals space 1 plus sinθ. space cosθ.

    Solution

    Solution not provided.

    Question 288
    CBSEENMA10008181
    Wired Faculty App

    Prove that: fraction numerator cos squared 20 degree plus cos squared 70 degree over denominator sin squared 20 degree space plus space sin squared 70 degree end fraction plus sin squared 64 degree plus cos 64 degree. space sin space 26 degree space equals space 2.

    Find the value of sin2 θ – cos2 θ.

    Solution

    Solution not provided.

    Question 289
    CBSEENMA10008182
    Wired Faculty App

    If square root of 3 space tan space straight theta space equals space 3 space sin space straight theta. Find the value of sin2 θ – cos2 θ.
    Solution

    Solution not provided.
    Ans. 1 third.

    Question 290
    CBSEENMA10008183
    Wired Faculty App

    Prove that:
    fraction numerator tanθ plus secθ minus 1 over denominator tanθ minus secθ plus 1 end fraction equals fraction numerator 1 plus sinθ over denominator cosθ end fraction.
    Solution

    Solution not provided.

    Question 291
    CBSEENMA10008184
    Wired Faculty App

    If tanθ space equals space 4 over 5 comma find the value of fraction numerator 2 space sinθ minus 3 cosθ over denominator 4 sinθ minus 9 cosθ end fraction.
    Solution

    Solution not provided.
    Ans. 7 over 29

    Question 293
    CBSEENMA10008186
    Wired Faculty App

    Prove the identity:  fraction numerator sinθ plus 1 minus cosθ over denominator cosθ minus 1 plus sinθ end fraction equals fraction numerator 1 plus sinθ over denominator cosθ end fraction.

    Solution

    Solution not provided.

    Question 294
    CBSEENMA10008187
    Wired Faculty App

    Prove the identity: (1 – sin θ + cos θ)2 = 2(1 + cos θ) (1 – sin θ).

    Solution

    Solution not provided.

    Question 295
    CBSEENMA10008188
    Wired Faculty App

    Evaluate:  4 left parenthesis sin to the power of 4 30 degree plus cos to the power of 4 60 degree right parenthesis minus 2 over 3 left parenthesis sin squared 60 degree minus cos squared 45 degree right parenthesis plus 1 half tan squared 60 degree

    Solution

    Solution not provided.
    Ans. 11 over 6

    Question 296
    CBSEENMA10008189
    Wired Faculty App

    Prove the identity:  square root of fraction numerator 1 plus cosθ over denominator 1 minus cosθ end fraction end root plus square root of fraction numerator 1 minus cosθ over denominator 1 plus cosθ end fraction end root space equals space 2 space cosecθ.

    Solution

    Solution not provided.

    Question 297
    CBSEENMA10008190
    Wired Faculty App

    Prove the identity:  square root of fraction numerator 1 plus sinθ over denominator 1 minus sinθ end fraction end root plus square root of fraction numerator 1 minus sinθ over denominator 1 plus sinθ end fraction end root space equals space 2 space secθ.

    Solution

    Solution not provided.

    Question 298
    CBSEENMA10008191
    Wired Faculty App

    Evaluate: 1 fourth open square brackets cot to the power of 4 30 degree minus cosec to the power of 4 60 degree close square brackets plus 3 over 2 left square bracket sec squared 45 degree minus tan squared 30 degree minus 5 cos squared 60 degree right square bracket.

    Solution

    Solution not provided.
    Ans. 11 over 6.

    Question 299
    CBSEENMA10008192
    Wired Faculty App

    Show that: fraction numerator tanθ plus secθ minus 1 over denominator tanθ minus secθ plus 1 end fraction equals fraction numerator 1 plus sinθ over denominator cos space straight theta end fraction.

    Solution

    Solution not provided.

    Question 301
    CBSEENMA10008194
    Wired Faculty App

    Without using trigonometric table, evaluate:
    cos space left parenthesis 40 degree plus straight theta right parenthesis minus sin left parenthesis 50 degree minus straight theta right parenthesis plus fraction numerator cos squared 40 degree plus cos squared 50 degree over denominator sin squared 40 degree plus sin squared 50 degree end fraction

    Solution

    Solution not provided.
    Ans. 1

    Question 302
    CBSEENMA10008195
    Wired Faculty App

    Evaluate: fraction numerator 2 space sin space 68 degree over denominator cos space 22 degree end fraction minus fraction numerator 2 space cot space 15 degree over denominator 5 space tan space 75 degree end fraction minus fraction numerator 3 space tan space 45 degree space tan space 20 degree space tan space 40 degree space tan space 50 degree space tan space 70 degree over denominator 5 end fraction
    Solution

    Solution not provided.
    Ans. 1

    Question 303
    CBSEENMA10008196
    Wired Faculty App

    Prove that: fraction numerator tanθ over denominator 1 minus cotθ end fraction plus fraction numerator cot space straight theta over denominator 1 minus tanθ end fraction space equals space 1 plus tanθ plus cotθ.
    Solution

    Solution not provided.

    Question 304
    CBSEENMA10008197
    Wired Faculty App

    Evaluate:
    fraction numerator 3 space tan space 25 degree. space tan space 40 degree. space tan space 50 degree. space tan space 65 degree. space minus space begin display style 1 half end style tan squared 60 degree over denominator 4 left parenthesis cos squared 29 degree space plus space cos squared 61 degree right parenthesis end fraction
    Solution

    Solution not provided.
    Ans. 3 over 8

    Question 305
    CBSEENMA10008198
    Wired Faculty App

    Evaluate:
    fraction numerator sin space 70 degree over denominator cos space 20 degree end fraction plus fraction numerator cosec space 36 degree over denominator sec space 54 degree end fraction minus fraction numerator 2 space cos space 43 degree. space cosec space 47 degree over denominator tan space 10 degree. space tan space 40 degree. space tan space 50 degree. space tan space 80 degree end fraction.
    Solution

    Solution not provided.

    Question 306
    CBSEENMA10008199
    Wired Faculty App

    Prove that: fraction numerator cosecA over denominator cosecA minus 1 end fraction plus fraction numerator cosecA over denominator cosecA plus 1 end fraction equals 2 plus 2 space tan squared straight A.
    Solution

    Solution not provided.

    Question 307
    CBSEENMA10008200
    Wired Faculty App

    Evaluate: fraction numerator secθ. space cosec space left parenthesis 90 degree minus straight theta right parenthesis space minus space tanθ. space cot space left parenthesis 90 degree minus straight theta right parenthesis plus sin squared 55 degree space plus space sin squared 55 degree over denominator tan space 10 degree. space tan space 20 degree. space tan space 60 degree. space tan space 70 degree. space tan space 80 degree end fraction
    Solution

    Solution not provided.
    Ans. fraction numerator 2 square root of 3 over denominator 3 end fraction

    Question 308
    CBSEENMA10008201
    Wired Faculty App

    Prove that:fraction numerator sinθ plus cosθ over denominator sinθ minus cosθ end fraction plus fraction numerator sinθ minus cosθ over denominator sinθ plus cosθ end fraction equals fraction numerator 2 space sec squared straight theta minus 1 over denominator tan squared straight theta minus 1 end fraction.
    Solution

    Solution not provided.


    Question 309
    CBSEENMA10008202
    Wired Faculty App

    Evaluate:
    fraction numerator sec squared left parenthesis 90 degree minus straight theta right parenthesis minus cot squared straight theta over denominator 2 left parenthesis sin squared space 25 degree space plus space sin squared space 65 degree right parenthesis end fraction plus fraction numerator 2 cos squared space 60 degree. space tan squared space 28 degree. space tan to the power of 2 space end exponent 62 degree over denominator 3 space left parenthesis sec squared space 43 degree space minus space cot squared space 47 degree right parenthesis end fraction

    Solution

    Solution not provided.
    Ans. 2 over 3


    Question 310
    CBSEENMA10008203
    Wired Faculty App

    Prove that: fraction numerator 1 plus cosθ over denominator 1 minus cosθ end fraction equals space left parenthesis cosecθ plus cotθ right parenthesis squared
    Solution

    Solution not provided.


    Question 311
    CBSEENMA10008204
    Wired Faculty App

    If 2 tanθ = 1. Find the value of fraction numerator 3 space cosθ plus 2 sinθ over denominator 2 cosθ minus sinθ end fraction

    Solution

    Solution not provided
    Ans. 8 over 3

    Question 312
    CBSEENMA10008205
    Wired Faculty App

    Prove that fraction numerator sinθ minus 2 sin cubed straight theta over denominator 2 cos cubed straight theta minus cosθ end fraction
    Solution

    Solution not provided.

    Question 313
    CBSEENMA10008206
    Wired Faculty App

    Prove that fraction numerator cosA over denominator 1 minus tanA end fraction plus fraction numerator sinA over denominator 1 minus cotA end fraction equals sinA plus cosA

    Solution

    Solution not provided.

    Question 314
    CBSEENMA10008207
    Wired Faculty App

    Prove that: (1 + cotθ – cosecθ) (1 + tanθ + secθ) = 2

    Solution

    Solution not provided.

    Question 315
    CBSEENMA10008208
    Wired Faculty App

    Prove that fraction numerator tanA plus secA minus 1 over denominator tanA minus secA plus 1 end fraction equals fraction numerator 1 plus sinA over denominator cosA end fraction

    Solution

    Solution not provided.

    Question 316
    CBSEENMA10008209
    Wired Faculty App

    Without using trigonometric tables, evaluate the following: 
    11 over 7. fraction numerator sin space 70 degree over denominator cos space 20 degree end fraction minus 4 over 7. space fraction numerator cos space 53 degree. space cosec space 37 degree over denominator tan space 15 degree. space tan space 35 degree. space tan space 55 degree. space tan space 75 degree end fraction

    Solution

    Solution not provided.

    Question 317
    CBSEENMA10008210
    Wired Faculty App

    Without using trigonometric tables, evaluate the following: 
    fraction numerator sin space 18 degree over denominator cos space 72 degree end fraction plus square root of 3 left square bracket tan space 10 degree space. space tan space 30 degree. space tan space 40 degree. space tan space 50 degree. space tan space 80 degree right square bracket

    Solution

    Solution not provided.
    Ans. 2

    Question 318
    CBSEENMA10008211
    Wired Faculty App

    Without using trigonometric tables, evaluate the following: 
    left parenthesis sin squared 25 degree space plus space sin squared 65 degree right parenthesis space plus space square root of 3 left parenthesis tan 5 degree. space tan 15 degree. space tan 30 degree. space tan 75 degree. space tan 85 degree. right parenthesis

    Solution

    Solution not provided.
    Ans. 2

    Question 320
    CBSEENMA10008213
    Wired Faculty App

    Without using trignometric tables, find the value of the following:
    open parentheses fraction numerator tan 20 degree over denominator cosec 70 degree end fraction close parentheses squared plus open parentheses fraction numerator cot space 20 degree over denominator sec space 70 degree end fraction close parentheses squared plus 2 tan 15 degree. space tan 45 degree. space tan 75 degree

    Solution

    Solution not provided.
    Ans. 3

    Question 321
    CBSEENMA10008214
    Wired Faculty App

    Without using trignometric tables, evaluate the following:
    fraction numerator cosec squared 65 degree minus tan squared 25 degree over denominator sin squared 17 degree plus sin squared 73 degree end fraction plus fraction numerator 1 over denominator square root of 3 end fraction left parenthesis tan space 10 degree. space tan space 30 degree. space tan space 80 degree. right parenthesis

    Solution

    Solution not provided.
    Ans. 4 over 3

    Question 322
    CBSEENMA10008215
    Wired Faculty App

    Without using trignometric tables, evaluate the following:
    2 open parentheses fraction numerator cos 58 degree over denominator sin 32 degree end fraction close parentheses minus square root of 3 open parentheses fraction numerator cos 35 degree. space cosec 52 degree over denominator tan space 15 degree. space tan 60 degree. space tan 75 degree end fraction close parentheses

    Solution

    Solution not provided.
    Ans. 1

    Question 323
    CBSEENMA10008216
    Wired Faculty App

    If sin3θ = cos (θ–6°) and 3θ and θ–6° are acute angles, find the value of θ.

    Solution

    Solution not provided.
    Ans. θ = 24°

    Question 324
    CBSEENMA10008217
    Wired Faculty App

    If 3 space cotθ space equals space 4 comma find the value of fraction numerator 5 space sin space straight theta space minus space 3 space cos space straight theta over denominator 5 space sinθ space plus space 3 space cosθ end fraction.
    Solution

    Solution not provided.
    Ans. 1 over 9

    Question 325
    CBSEENMA10008218
    Wired Faculty App

    If tanA space equals space 5 over 12 comma find the value of left parenthesis sinA plus cosA right parenthesis space secA.
    Solution

    Solution not provided.
    Ans. 17 over 12

    Question 326
    CBSEENMA10008219
    Wired Faculty App

    If sec4A = cosec (A - 20) where 4A is an acute angle, find the value of A.

    Solution

    Solution not provided.
    Ans. 22 degree

    Question 327
    CBSEENMA10008220
    Wired Faculty App

    In a ΔABC, right angled at C, if tanA space equals space fraction numerator 1 over denominator square root of 3 end fraction comma find the value of sinA.cosB+cosA.sinB.

    Solution

    Solution not provided.
    Ans. 1

    Question 328
    CBSEENMA10008221
    Wired Faculty App

    If sec2A = cosec (A - 42)where 2A is an acute angle, find the value of A.

    Solution

    Solution not provided.
    Ans. 44 degree

    Question 329
    CBSEENMA10008222
    Wired Faculty App

    In ΔABC, right angled at A, if tanC space equals space square root of 3 comma find the value of sinB.cosC+cosB sinC.

    Solution

    Solution not provided.
    Ans. 1

    Question 330
    CBSEENMA10008223
    Wired Faculty App

    Prove that: fraction numerator cotA minus cosA over denominator cotA plus cosA end fraction equals fraction numerator cosecA minus 1 over denominator cosecA plus 1 end fraction
    Solution

    Solution not provided.

    Question 331
    CBSEENMA10008224
    Wired Faculty App

    Prove that: (1+cotA-cosecA) (1+tanA+secA) = 2

    Solution

    Solution not provided.

    Question 332
    CBSEENMA10008225
    Wired Faculty App

    Prove that: (sinθ + cosecθ)2 + (cosθ + secθ)2 = 7 + tan2θ + cot2θ.

    Solution

    Solution not provided.

    Question 333
    CBSEENMA10008226
    Wired Faculty App

    Prove that: sinθ (1+tanθ) + cos θ (1+cotθ) = secθ + cosecθ

    Solution

    Solution not provided.

    Question 334
    CBSEENMA10008227
    Wired Faculty App

    If 7 space sin squared straight theta space plus space 3 space cos squared straight theta space equals space 4. Show that tanθ space equals space fraction numerator 1 over denominator square root of 3 end fraction
    Solution

    Solution not provided.

    Question 335
    CBSEENMA10008228
    Wired Faculty App

    Prove that fraction numerator cosθ minus sinθ plus 1 over denominator cosθ plus sinθ minus 1 end fraction equals cosecθ plus cotθ
    Solution

    Solution not provided.

    Question 336
    CBSEENMA10008229
    Wired Faculty App

    Prove that: open parentheses cosecθ minus sinθ close parentheses space left parenthesis sinθ minus cosθ right parenthesis space equals space fraction numerator 1 over denominator tanθ plus cotθ end fraction
    Solution

    Solution not provided.

    Question 337
    CBSEENMA10008230
    Wired Faculty App

    Prove that: fraction numerator cosecA over denominator cosecA minus 1 end fraction plus fraction numerator cosecA over denominator cosecA plus 1 end fraction equals 2 sec squared straight A
    Solution

    Solution not provided.

    Question 338
    CBSEENMA10008231
    Wired Faculty App

    Prove that: fraction numerator 1 over denominator secA plus tanA end fraction minus 1 over cosA equals 1 over cosA minus fraction numerator 1 over denominator secA minus tanA end fraction
    Solution

    Solution not provided.

    Question 339
    CBSEENMA10008232
    Wired Faculty App

    If sinθ equals 1 third comma find the value of (2 cot2 θ = 2).
    Solution

    Solution not provided.
    Ans. 18

    Question 340
    CBSEENMA10008233
    Wired Faculty App

    Simplify:  fraction numerator sin cubed straight theta plus cos cubed straight theta over denominator sinθ plus cosθ end fraction plus sinθ. space cosθ
    Solution

    Solution not provided.
    Ans. 1

    Question 341
    CBSEENMA10008234
    Wired Faculty App

    Find the value of sin 30° geometrically.

    Solution

    Solution not provided.
    Ans. 1 half

    Question 342
    CBSEENMA10008235
    Wired Faculty App

    Without using trigonometric table, evaluate: 
    fraction numerator cos space 58 degree over denominator sin space 32 degree end fraction plus fraction numerator sin space 22 degree over denominator cos space 68 degree end fraction minus fraction numerator cos space 38 degree. space cosec 32 degree over denominator tan 18 degree. tan 35 degree. space tan 60 degree. space tan space 72 degree. tan 55 degree end fraction

    Solution

    Solution not provided.
    Ans. fraction numerator 2 square root of 3 minus 1 over denominator square root of 3 end fraction

    Question 343
    CBSEENMA10008236
    Wired Faculty App

    If sec2 θ = (1 + sin θ) (1 – sin θ) = k, then find the value of k.

    Solution

    Solution not provided.
    Ans. k = 1

    Question 344
    CBSEENMA10008237
    Wired Faculty App

    If cot space straight theta space equals space 15 over 8 comma then evaluate fraction numerator left parenthesis 2 plus 2 sinθ right parenthesis space left parenthesis 1 minus sinθ right parenthesis over denominator left parenthesis 1 plus cosθ right parenthesis space left parenthesis 2 minus 2 cosθ right parenthesis end fraction
    Solution

    Solution not provided.
    Ans. 225 over 64

    Question 345
    CBSEENMA10008238
    Wired Faculty App

    Find the value of tan 60°, geometrically.

    Solution

    Solution not provided.
    Ans. square root of 3

    Question 346
    CBSEENMA10008239
    Wired Faculty App

    Evaluate: 2 over 3 cosec squared 58 degree minus 2 over 3 cot space 58 degree. space tan space 32 degree minus 5 over 3 space tan space 13 degree. space tan 37 degree. space tan space 45 degree. tan 53 degree. space tan 77 degree.
    find the value of cosec B.

    Solution

    Solution not provided.
    Ans. -1

    Question 347
    CBSEENMA10008240
    Wired Faculty App

    If secA space equals space 15 over 7 space and space straight A plus straight B space equals space 90 degree comma find the value of cosec B.
    Solution

    Solution not provided.
    Ans. 15 over 7

    Question 348
    CBSEENMA10008241
    Wired Faculty App

    Without using trigonometric tables, evaluate: 
    fraction numerator 7 space cos space 70 degree over denominator 2 space sin space 20 degree end fraction plus 3 over 2 fraction numerator cos space 55 degree. space cosec space 35 degree over denominator tan space 5 degree. space tan 25 degree. space tan 45 degree. space tan 85 degree. space tan space 65 degree end fraction

    Solution

    Solution not provided.
    Ans. 5

    Question 349
    CBSEENMA10008242
    Wired Faculty App

    Prove that: sec squared straight theta minus fraction numerator sin squared straight theta minus 2 sin to the power of 4 straight theta over denominator 2 cos to the power of 4 straight theta minus cos squared straight theta end fraction equals 1.
    Solution

    Solution not provided.

    Question 350
    CBSEENMA10008243
    Wired Faculty App

    If secθ space equals space 25 over 7 comma then the values of tan θ is

    • 7 over 24
    • 27 over 7
    • 24 over 7
    • 22 over 7

    Solution

    C.

    24 over 7

    Tips: -

    secθ space equals space OP over OQ equals 25 over 7 comma space space space sec squared straight theta space equals space 1 plus tan squared straight theta rightwards double arrow space space space space open parentheses 25 over 7 close parentheses squared minus 1 space equals space tan squared straight theta space equals space fraction numerator 625 minus 49 over denominator 49 end fraction equals tan squared straight theta rightwards double arrow space space tan space straight theta space equals space square root of 576 over 49 end root space equals space 24 over 7 space space space Ans. space left parenthesis straight c right parenthesis
    Question 351
    CBSEENMA10008244
    Wired Faculty App

    The value of fraction numerator 5 space sin squared 30 degree plus cos squared 45 degree plus 4 space tan squared space 60 degree over denominator 2 space sin space 30 degree space cos space 60 degree space plus space tan space 45 degree end fraction is

    • 9 1 over 6
    • 8 1 fifth
    • 5 2 over 6
    • 4 1 over 6

    Solution

    A.

    9 1 over 6
    Question 352
    CBSEENMA10008245
    Wired Faculty App

    If cos (40° + x) = sin 30° the value of x is
    • 30°
    • 40°
    • 20°
    • 60°

    Solution

    C.

    20°

    Tips: -

    cos (40 + x) = sin 30° = sin (90° – 60°) ⇒ cos (40° + x) = cos 60° ⇒ x = 20°.
    Question 353
    CBSEENMA10008246
    Wired Faculty App

    If sinθ space equals space 3 over 5 comma space find space the space value space of space left parenthesis tan space straight theta space plus space sec space straight theta right parenthesis 2.

    • 3

    • 6

    • 2

    • 4
    Solution

    D.

    4

    Question 354
    CBSEENMA10008247
    Wired Faculty App

    If 3 tan θ = 4, find the value of fraction numerator 5 space sin space straight theta minus 3 cosθ over denominator 5 space sinθ plus 2 space cosθ end fraction
    • 11 over 26
    • 26 over 11
    • 12 over 25
    • 15 over 28

    Solution

    A.

    11 over 26 fraction numerator 5 space sinθ minus 3 space cosθ over denominator 5 space sinθ space plus 2 space cosθ end fraction equals fraction numerator 5 begin display style sinθ over cosθ end style minus 3 begin display style cosθ over cosθ end style over denominator 5 begin display style sinθ over sinθ end style plus 2 begin display style cosθ over cosθ end style end fraction space rightwards double arrow space space fraction numerator 5 space tanθ minus 3 over denominator 5 space tanθ plus 2 end fraction equals fraction numerator 5 cross times begin display style 4 over 3 end style minus 3 over denominator 5 cross times begin display style 4 over 3 end style plus 2 end fraction equals fraction numerator 20 minus 9 over denominator 20 plus 6 end fraction equals 11 over 26
    Question 355
    CBSEENMA10008248
    Wired Faculty App

    Without using trigonometric tables, evaluate:
    2 fraction numerator sin space 43 degree over denominator cos space 47 degree end fraction minus fraction numerator cot space 30 degree over denominator tan space 60 degree end fraction minus square root of 2 space sin space 45 degree
    • 0
    • 2
    • 4
    • 1

    Solution

    A.

    0 2 space fraction numerator sin space 43 degree over denominator cos space 47 degree end fraction minus fraction numerator cot space 30 degree over denominator tan space 60 degree end fraction minus square root of 2 space sin space 45 degree comma space space space 2 fraction numerator sin left parenthesis 90 degree minus 47 degree right parenthesis over denominator cos space 47 degree end fraction minus fraction numerator cot space left parenthesis 90 degree minus 60 degree right parenthesis over denominator tan space 60 degree end fraction minus square root of 2 cross times 1 half space rightwards double arrow space space space 2. space fraction numerator cos space 47 degree over denominator cos space 47 degree end fraction minus fraction numerator tan space 60 degree over denominator tan space 60 degree end fraction minus 1 space equals space 2 minus 1 minus 1 space equals space 0
    Question 356
    CBSEENMA10008249
    Wired Faculty App

    Without using trigonometric tables, evaluate: fraction numerator cos squared 20 degree plus cos squared 70 degree over denominator sin squared 59 degree plus sin squared 31 degree end fraction
    • 2

    • 0

    • 1

    • -1
    Solution

    C.

    1

    fraction numerator cos left parenthesis 90 degree minus 70 degree right parenthesis plus cos squared 70 degree over denominator sin squared left parenthesis 90 degree minus 31 degree right parenthesis plus sin squared 31 degree end fraction equals fraction numerator sin squared 20 degree plus cos squared 70 degree over denominator cos squared 31 degree plus sin squared 31 degree end fraction space equals space 1
    Question 357
    CBSEENMA10008250
    Wired Faculty App

    The value of : sin (50° + 0) - cos (40° - 0) is
    • 2
    • 1

    • -1

    • 0
    Solution

    D.

    0

    Question 358
    CBSEENMA10008251
    Wired Faculty App

    The value of: fraction numerator cot space 40 degree over denominator tan space 50 degree end fraction minus 1 half open parentheses fraction numerator cos space 35 degree over denominator sin space 55 degree end fraction close parentheses is

    • 1 half
    • negative 1 half
    • 2 over 3
    • 2 over 5

    Solution

    A.

    1 half
    Question 359
    CBSEENMA10008252
    Wired Faculty App

    Evaluate: fraction numerator secθ. cosec left parenthesis 90 degree minus straight theta right parenthesis minus tanθ space cot left parenthesis 90 degree minus straight theta right parenthesis plus sin squared 55 degree space plus space sin squared 35 degree over denominator tan space 10 degree space tan space 20 degree space tan space 60 degree space tan space 70 degree space tan space 80 degree end fraction

    • fraction numerator 1 over denominator square root of 3 end fraction
    • fraction numerator 2 over denominator square root of 3 end fraction
    • 2 over 3
    • fraction numerator 3 over denominator square root of 2 end fraction

    Solution

    B.

    fraction numerator 2 over denominator square root of 3 end fraction fraction numerator secθ space cosec space straight theta left parenthesis 90 degree minus straight theta right parenthesis space minus space tanθ space cot left parenthesis 90 degree minus straight theta right parenthesis plus sin squared 55 degree plus sin squared 35 degree over denominator tan 10 degree space tan 20 degree space tan 60 degree tan 70 degree space tan space 80 degree end fraction equals space fraction numerator left parenthesis sec squared straight theta minus tan squared straight theta right parenthesis plus left parenthesis cos squared 35 degree plus sin squared 35 degree right parenthesis over denominator left parenthesis tan 10 degree tan 80 degree right parenthesis space left parenthesis tan 20 degree space tan 70 degree right parenthesis. space tan 60 degree end fraction left square bracket secθ space equals space cosec left parenthesis 90 degree minus straight theta right parenthesis comma space cosθ space equals space sin left parenthesis 90 degree minus straight theta right parenthesis right square bracket equals space fraction numerator 1 plus 1 over denominator 1 cross times 1 cross times square root of 3 end fraction equals fraction numerator 2 over denominator square root of 3 end fraction left square bracket tan 10 degree space equals space cot space 80 degree comma space tan 20 degree space equals space cot 70 degree comma space tanθ cross times cotθ equals 1 right square bracket
    Question 360
    CBSEENMA10008253
    Wired Faculty App

    If secα space equals space 5 over 4 comma space then space the space value space of space sinα over secα is

    • 1 fifth
    • 2 over 5
    • 3 over 5
    • 4 over 5

    Solution

    C.

    3 over 5
    Question 361
    CBSEENMA10008254
    Wired Faculty App

    Given that 16 cot A = 12, then the value of fraction numerator sinA plus cosA over denominator sinA minus cosA end fraction is

    • 5

    • 6

    • 8

    • 7
    Solution

    D.

    7

    Question 362
    CBSEENMA10008255
    Wired Faculty App

    The value of x if tan 3x = (sin 45° . cos 45°) sin 30°:
    • 14°
    • 15°
    • 16°
    • 20°

    Solution

    B.

    15° tan 3 straight x space equals space open parentheses fraction numerator 1 over denominator square root of 2 end fraction cross times fraction numerator 1 over denominator square root of 2 end fraction close parentheses divided by 1 half equals 1 half cross times 2 over 1 equals 1 equals tan 45 degree comma space space 3 straight x space equals space 45 degree space space rightwards double arrow space straight x space equals space 15 degree
    Question 364
    CBSEENMA10008257
    Wired Faculty App

    The value of (1 + cot2 θ) (1 – cos θ) (1 + cos θ ) is

    • 2

    • 1
    • 5
    • 6

    Solution

    D.

    6
    Question 365
    CBSEENMA10008258
    Wired Faculty App

    The value of fraction numerator cosA over denominator 1 minus tanA end fraction plus fraction numerator sinA over denominator 1 minus cotA end fraction is

    • cos A + sin A
    • sin A – cos A 
    • tan A + cot A
    • cos A - sin A

    Solution

    A.

    cos A + sin A
    Question 366
    CBSEENMA10008259
    Wired Faculty App

    tan 10°. tan 75°. tan 15°. tan 80° is
    • 0
    • 3
    • 1

    • 2
    Solution

    C.

    1
    Question 367
    CBSEENMA10008260
    Wired Faculty App

    tan 1°. tan 2°. tan 3°................tan 89° is
    • 1

    • 0

    • 4

    • 5
    Solution

    A.

    1
    Question 368
    CBSEENMA10008261
    Wired Faculty App

    open parentheses fraction numerator tan space 20 degree over denominator cosec space 70 degree end fraction close parentheses squared plus open parentheses fraction numerator cot space 20 degree over denominator sec space 70 degree end fraction close parentheses squared is

    • 6

    • 1 half

    • 0

    • 1
    Solution

    D.

    1

    Question 370
    CBSEENMA10008263
    Wired Faculty App

    Prove the following identity:
    2 (sin6θ + cos6θ) -3 (sin4θ + cos4θ) + 1 = 0

    Solution

    L.H..S. = space 2 left parenthesis sin to the power of 6 straight theta plus cos to the power of 6 straight theta right parenthesis space minus space 3 left parenthesis sin to the power of 4 straight theta plus cos to the power of 4 straight theta right parenthesis plus 1
              equals 2 left square bracket left parenthesis sin squared straight theta right parenthesis cubed plus left parenthesis cos squared straight theta right parenthesis cubed right square bracket minus 3 left square bracket left parenthesis sin squared straight theta right parenthesis squared plus left parenthesis cos squared straight theta right parenthesis squared right square bracket plus 1 equals 2 left square bracket left parenthesis sin squared straight theta plus cos squared straight theta right parenthesis space minus space 3 space sin squared straight theta. space cos squared straight theta right square bracket space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space minus 3 left square bracket left parenthesis sin squared straight theta plus cos squared straight theta right square bracket squared equals space 2 left square bracket left parenthesis 1 right parenthesis cubed minus 3 sin squared straight theta. space cos squared straight theta right square bracket space minus 3 space left square bracket 1 minus 2 sin squared cos squared straight theta right square bracket plus 1 equals 2 space left parenthesis 1 minus 3 sin squared straight theta. space cos squared straight theta right parenthesis space minus 3 space left parenthesis 1 minus 2 sin squared cos squared straight theta right square bracket plus 1

    Question 371
    CBSEENMA10008264
    Wired Faculty App

    Prove the following identity:
    fraction numerator sinA minus sinB over denominator cosA plus cosB end fraction plus fraction numerator cosA minus cosB over denominator sinA plus sinB end fraction equals 0.

    Solution

    L.H.S. = fraction numerator sinA minus sinB over denominator cosA plus cosB end fraction plus fraction numerator cosA plus cosB over denominator sinA plus sinB end fraction
     = fraction numerator left parenthesis sin squared straight A minus sin squared straight B right parenthesis plus left parenthesis cos squared straight A minus cos squared straight B right parenthesis over denominator left parenthesis cosA plus cosB right parenthesis thin space left parenthesis sinA plus sinB right parenthesis end fraction
         equals space fraction numerator left parenthesis sin squared straight A plus cos squared straight A right parenthesis space minus space left parenthesis sin squared straight B plus cos squared straight B right parenthesis over denominator left parenthesis cosA plus cosB right parenthesis thin space left parenthesis sinA plus sinB right parenthesis end fraction equals space fraction numerator 1 minus 1 over denominator left parenthesis cosA plus cosB right parenthesis space left parenthesis sinA plus sinB right parenthesis end fraction equals space fraction numerator 0 over denominator left parenthesis cosA plus cosB right parenthesis thin space left parenthesis sinA plus sinB right parenthesis end fraction equals space 0. space equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
              

    Question 372
    CBSEENMA10008265
    Wired Faculty App

    Prove the following identity:
    tan squared straight A minus tan squared straight B space equals space fraction numerator sin squared straight A minus sin squared straight B over denominator cos squared straight A cross times cos squared straight B end fraction.

    Solution
    tan squared straight A minus tan squared straight B space equals space fraction numerator sin squared straight A minus sin squared straight B over denominator cos squared straight A. space cos squared straight B end fraction
    L.H.S. = tan squared straight A minus tan squared straight B
              equals space fraction numerator sin squared straight A over denominator cos squared straight A end fraction minus fraction numerator sin squared straight B over denominator cos squared straight B end fraction equals space fraction numerator sin squared straight A. space cos squared straight B space minus space sin squared straight B. space cos squared straight A over denominator cos squared straight A. space cos squared straight B end fraction equals space fraction numerator sin squared straight A left parenthesis 1 minus sin squared straight B right parenthesis space minus space sin squared straight B left parenthesis 1 minus sin squared straight A right parenthesis over denominator cos squared straight A. space cos squared straight B end fraction

    equals space fraction numerator space sin squared straight A minus sin squared straight A. space sin squared straight B space minus space sin squared straight B plus sin squared straight B. sin squared straight A over denominator cos squared straight A. space cos squared straight B end fraction equals space fraction numerator sin squared straight A minus sin squared straight B over denominator cos squared straight A. space cos squared straight B end fraction space equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
    Question 373
    CBSEENMA10008266
    Wired Faculty App

    Prove the following identity:
    left parenthesis secA minus tanA right parenthesis squared space left parenthesis 1 plus sinA right parenthesis space equals space 1 minus space sinA.

    Solution

    L.H.S. = left parenthesis secA minus tanA right parenthesis squared space left parenthesis 1 plus sinA right parenthesis
         space equals space open parentheses 1 over cosA minus sinA over cosA close parentheses squared space left parenthesis 1 plus sinA right parenthesis equals space open parentheses fraction numerator 1 minus sinA over denominator cosA end fraction close parentheses squared space left parenthesis 1 plus sinA right parenthesis space equals space fraction numerator left parenthesis 1 minus sinA right parenthesis squared over denominator cos squared straight A end fraction left parenthesis 1 plus sinA right parenthesis equals space fraction numerator left parenthesis 1 minus sinA right parenthesis squared over denominator 1 minus sin squared straight A end fraction left parenthesis 1 plus sinA right parenthesis space equals space fraction numerator left parenthesis 1 minus sinA right parenthesis squared space left parenthesis 1 plus sinA right parenthesis over denominator left parenthesis 1 minus sinA right parenthesis thin space left parenthesis 1 plus sinA right parenthesis end fraction space equals space 1 minus sinA space equals space straight R. straight H. straight S.

    Question 374
    CBSEENMA10008267
    Wired Faculty App

    Prove the following identity:
    sec to the power of 6 straight theta space equals space tan to the power of 6 straight theta space plus space 3 space tan space straight theta. space secθ plus 1

    Solution

     sec to the power of 6 straight theta space equals space tan to the power of 6 straight theta plus 3 tanθ. space secθ space plus 1 straight L. straight H. straight S. equals space sec to the power of 6 straight theta space equals space left parenthesis sec squared straight theta right parenthesis cubed space space space space space space space space space space space equals space left parenthesis tan squared straight theta plus 1 right parenthesis cubed space space space space space space space space space space space space equals space left parenthesis tan squared straight theta right parenthesis cubed space plus space left parenthesis 1 right parenthesis cubed plus 3 left parenthesis tan squared straight theta right parenthesis space left parenthesis 1 right parenthesis space left parenthesis tan squared straight theta plus 1 right parenthesis space space space space space space space space space space space space equals space tan to the power of 6 straight theta space plus space 1 plus 3 tan squared straight theta. space sec squared straight theta space space space space space space space space space space space space space space space equals straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.

    Question 375
    CBSEENMA10008268
    Wired Faculty App

    Prove the following identity:
    left parenthesis 1 plus tan squared straight theta right parenthesis plus open parentheses 1 plus fraction numerator 1 over denominator tan squared straight theta end fraction close parentheses space equals fraction numerator 1 over denominator sin squared straight theta minus sin to the power of 4 straight theta end fraction

    Solution

    L.H.S. = left parenthesis 1 plus tan squared straight theta right parenthesis plus open parentheses 1 plus fraction numerator 1 over denominator tan squared straight theta end fraction close parentheses
                equals space left parenthesis 1 plus tan squared straight theta right parenthesis space plus space left parenthesis 1 plus cot squared straight theta right parenthesis space equals sec squared straight theta space plus space cosec squared straight theta space equals space fraction numerator 1 over denominator cos squared straight theta end fraction plus fraction numerator 1 over denominator sin squared straight theta end fraction space equals space fraction numerator sin squared straight theta plus cos squared straight theta over denominator cos squared straight theta. space sin squared straight theta end fraction equals space fraction numerator sin squared straight theta plus cos squared straight theta over denominator left parenthesis 1 minus sin squared straight theta right parenthesis space sin squared straight theta end fraction space equals space fraction numerator 1 over denominator sin squared straight theta minus sin to the power of 4 straight theta end fraction equals straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.

    Question 376
    CBSEENMA10008269
    Wired Faculty App

    Prove the following identity:
    left parenthesis 1 plus tanA. tanB right parenthesis squared plus left parenthesis tanA minus tanB right parenthesis squared space equals sec squared straight A. space sec squared straight B.

    Solution

    L.H.S 
     equals space left parenthesis 1 plus tanA. space tanB right parenthesis squared plus left parenthesis tanA minus tanB right parenthesis squared equals space left parenthesis 1 plus tan squared straight A. space tan squared straight B space plus space 2 space tanA. space tanB space plus space tan squared straight A space plus space tan squared straight B space minus space 2 space tanA. space tanB right parenthesis equals space 1 plus tan squared straight A plus tan squared straight B plus tan squared straight A. space tan squared straight B equals space left parenthesis 1 plus tan squared straight A right parenthesis plus space tan squared straight B left parenthesis 1 plus tan squared straight A right parenthesis equals space left parenthesis 1 plus tan squared straight B right parenthesis thin space left parenthesis 1 plus tan squared straight A right parenthesis equals space sec squared straight B. space sec squared straight A equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.

    Question 377
    CBSEENMA10008270
    Wired Faculty App

    Prove the following identity:
    cotθ minus tanθ space equals space fraction numerator 2 space cos squared straight theta minus 1 over denominator sinθ minus cosθ end fraction.

    Solution
    cot space straight theta space minus space tanθ space equals space fraction numerator 2 space cos squared straight theta minus 1 over denominator sinθ. space cosθ end fraction
    L.H.S. = cot space straight theta space minus space tanθ
    equals space cosθ over sinθ minus sinθ over cosθ equals fraction numerator cos squared straight theta minus sin squared straight theta over denominator sinθ. space cosθ end fraction equals space fraction numerator cos squared straight theta minus left parenthesis 1 minus cos squared straight theta right parenthesis over denominator sinθ. space cosθ end fraction space equals space fraction numerator cos squared straight theta minus 1 plus cos squared straight theta over denominator sinθ. space cosθ end fraction equals space fraction numerator 2 space cos squared straight theta minus 1 over denominator sinθ. space cosθ end fraction space equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
    Question 378
    CBSEENMA10008271
    Wired Faculty App

    Prove the following identity:
    tan squared straight theta plus cot squared straight theta plus 2 space equals space sec squared straight theta. space cosec squared straight theta.

    Solution
    tan squared straight theta plus cot squared straight theta plus 2 equals sec squared straight theta. space cosec squared straight theta
    L.H.S. = tan squared straight theta plus cot squared straight theta plus 2
               equals space fraction numerator sin squared straight theta over denominator cos squared straight theta end fraction plus fraction numerator cos squared straight theta over denominator sin squared straight theta end fraction plus 2
                equals space fraction numerator sin to the power of 4 straight theta plus cos to the power of 4 straight theta plus 2 sin squared straight theta. space cos squared straight theta over denominator cos squared straight theta. space sin squared straight theta end fraction equals space fraction numerator left parenthesis sin squared straight theta right parenthesis squared plus left parenthesis cos squared straight theta right parenthesis squared plus 2 sin squared straight theta. space cos squared straight theta over denominator blank end fraction equals space fraction numerator left parenthesis sin squared straight theta plus cos squared straight theta right parenthesis squared over denominator cos squared straight theta. space sin squared straight theta end fraction space equals fraction numerator 1 over denominator cos squared straight theta. space sin squared straight theta end fraction equals space sec squared straight theta. space cosec squared straight theta space equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
    Question 379
    CBSEENMA10008272
    Wired Faculty App

    Prove the following identity:
    left parenthesis 1 plus cotA plus tanA right parenthesis space left parenthesis sinA minus cosA right parenthesis space equals space sinA. space tanA minus space cotA. space cosA.

    Solution

    L.H.S. = (1+ cot A + tan A) (sin A - cos A)
    equals open parentheses 1 plus cosA over sinA plus sinA over cosA close parentheses space left parenthesis sinA minus cosA right parenthesis equals space open parentheses 1 plus fraction numerator cos squared straight A plus sin squared straight A over denominator sinA space cosA end fraction close parentheses space left parenthesis sinA minus cosA right parenthesis equals open parentheses 1 plus fraction numerator 1 over denominator sinA space cosA end fraction close parentheses space left parenthesis sinA space minus space cosA right parenthesis equals space open parentheses fraction numerator sinA. space cosA space plus 1 over denominator sinA space cosA end fraction close parentheses space left parenthesis sinA space minus space cosA right parenthesis equals space fraction numerator left parenthesis sinA minus cosA right parenthesis space left parenthesis 1 plus sinA space cosA right parenthesis over denominator sinA space cosA end fraction straight R. straight H. straight S. space equals space sinA. space tanA space minus space cotA space cosA
    equals space sinA. space sinA over cosA minus cosA over sinA. cosA equals space fraction numerator sin squared straight A over denominator cosA end fraction minus fraction numerator cos squared straight A over denominator sinA end fraction equals fraction numerator sin cubed straight A minus cos cubed straight A over denominator sinA space cosA end fraction equals space fraction numerator left parenthesis sinA minus cosA right parenthesis space left parenthesis sin squared straight A plus cos squared straight A plus sinA. space cosA right parenthesis over denominator sinA. space cosA end fraction equals space fraction numerator left parenthesis sinA minus cosA right parenthesis left parenthesis 1 plus sinA space cosA right parenthesis over denominator sinA. cosA end fraction
    L.H.S. = R.H.S.
    Hence, (1 + cot A + tan A) (sin A - cos A) = sin A . tan A - cot A . cos A Proved

    Question 380
    CBSEENMA10008273
    Wired Faculty App

    If 7 sin2θ + 3cos2θ = 4, show that tanθ space equals space fraction numerator 1 over denominator square root of 3 end fraction.

    Solution

    We have,
      7 space sin squared straight theta plus 3 space cos squared straight theta space equals space 4
    rightwards double arrow space space 4 space sin squared straight theta plus 3 space sin squared straight theta plus 3 cos squared straight theta space equals space 4 rightwards double arrow space space 4 space sin squared straight theta space plus space 3 space left parenthesis sin squared straight theta space plus space cos squared straight theta right parenthesis space equals space 4 rightwards double arrow space 4 space sin squared straight theta space plus space 3 cross times 1 space equals space 4 rightwards double arrow space 4 space sin squared straight theta space equals space 4 space minus 3 rightwards double arrow space 4 space sin squared straight theta space equals space 1 rightwards double arrow space space sin squared straight theta space equals space 1 fourth
     And comma space cos squared straight theta space equals space 1 minus sin squared straight theta. space space space space space space space space space space space equals space 1 minus 1 fourth equals 3 over 4 Now comma space fraction numerator sin squared straight theta over denominator cos squared straight theta end fraction equals 1 third rightwards double arrow space tan squared straight theta space equals space 1 third rightwards double arrow space tanθ space equals space fraction numerator 1 over denominator square root of 3 end fraction

    Question 382
    CBSEENMA10008275
    Wired Faculty App

    Prove that:
    sec squared straight theta minus fraction numerator sin squared straight theta minus 2 sin to the power of 4 straight theta over denominator 2 space cos to the power of 4 straight theta space minus cos squared straight theta end fraction equals 1
    Solution
    straight L. straight H. straight S. space equals space sec squared straight theta minus fraction numerator sin squared straight theta minus 2 sin to the power of 4 straight theta over denominator 2 cos to the power of 4 straight theta minus cos squared straight theta end fraction equals space sec squared straight theta minus fraction numerator sin squared straight theta space left parenthesis 1 minus 2 sin squared straight theta right parenthesis over denominator cos squared straight theta left parenthesis 2 cos squared straight theta minus 1 right parenthesis end fraction equals space sec squared straight theta space minus space fraction numerator sin squared straight theta open square brackets 1 minus 2 open parentheses 1 minus cos squared straight theta close parentheses close square brackets over denominator cos squared straight theta space left parenthesis 2 cos squared straight theta minus 1 right parenthesis end fraction equals space sec squared straight theta space minus tan squared straight theta fraction numerator left parenthesis 1 minus 2 plus 2 cosθ right parenthesis over denominator 2 space cosθ minus 1 end fraction space equals space sec squared straight theta space minus tan squared straight theta space open parentheses fraction numerator 2 cos squared straight theta minus 1 over denominator 2 cos squared straight theta minus 1 end fraction close parentheses equals space sec squared straight theta space minus space tan squared straight theta space equals space 1 space equals space straight R. straight H. straight S.
    Question 383
    CBSEENMA10008276
    Wired Faculty App

    If fraction numerator tan space straight A over denominator tan space straight B end fraction equals straight n space and space fraction numerator sin space straight A over denominator sin space straight B end fraction equals straight m comma then show that cos squared straight A space equals space fraction numerator straight m squared minus 1 over denominator straight n squared minus 1 end fraction.
    Solution
    space space space space space space space space space space space space space tanA space equals space straight n space tan space straight B rightwards double arrow space space space space space space space space tan space straight B space equals space 1 over straight n tanA rightwards double arrow space space space space space space space space cot space straight B space equals space fraction numerator straight n over denominator tan space straight A end fraction
     and space space space space sin space straight A space equals space straight m space sinB rightwards double arrow space space space space space space sin space straight B space equals space 1 over straight m sinA rightwards double arrow space space space space space space cosecB space equals space fraction numerator straight m over denominator sin space straight A end fraction
    Substituting the values of cot B and cosec B in cosec2 B - cot2 B = 1, we get
    rightwards double arrow space space space space space space space space space fraction numerator straight m squared over denominator sin squared straight A end fraction minus fraction numerator straight n squared over denominator tan squared straight A end fraction equals 1 rightwards double arrow space space space space space fraction numerator straight m squared over denominator sin squared straight A end fraction minus fraction numerator straight n squared space cos squared straight A over denominator sin squared straight A end fraction equals 1 rightwards double arrow space space space space space space space fraction numerator straight m squared minus straight n squared space cos squared straight A over denominator sin squared straight A end fraction equals 1 rightwards double arrow space space space space space space space space space space space straight m squared minus straight n squared cos squared straight A space equals space sin squared straight A rightwards double arrow space space space space space space space space space space space space straight m squared minus straight n squared cos squared straight A space equals space 1 minus cos squared straight A rightwards double arrow space space space space space space space space space space space space straight m squared minus 1 space equals space straight n squared cos squared straight A space minus space cos squared straight A rightwards double arrow space space space space space space space space space space space space fraction numerator straight m squared minus 1 over denominator straight n squared minus 1 end fraction equals cos squared straight A
    Question 384
    CBSEENMA10008277
    Wired Faculty App

    Prove the following identity:
    fraction numerator 1 over denominator secθ minus tanθ end fraction minus 1 over cosθ space equals space 1 over cosθ minus fraction numerator 1 over denominator secθ plus tanθ end fraction.
    Solution
    fraction numerator 1 over denominator secθ minus tanθ end fraction minus 1 over cosθ space equals space 1 over cosθ minus fraction numerator 1 over denominator secθ plus tanθ end fraction
    straight L. straight H. straight S. space equals space fraction numerator 1 over denominator secθ minus tanθ end fraction minus 1 over cosθ space space space space space space space space space space space space space equals space open parentheses fraction numerator 1 over denominator secθ minus tanθ end fraction cross times fraction numerator secθ plus tanθ over denominator secθ plus tanθ end fraction close parentheses minus 1 over cosθ space space space space space space space space space space space space space equals open parentheses fraction numerator secθ plus tanθ over denominator sec squared straight theta minus tan squared straight theta end fraction close parentheses minus secθ space space space space space space space space space space space space space space equals space secθ plus tanθ minus secθ space equals space tanθ
    straight R. straight H. straight S. equals space 1 over cosθ minus fraction numerator 1 over denominator secθ plus tanθ end fraction space space space space space space space space space space space space space equals space 1 over cosθ minus open parentheses fraction numerator 1 over denominator secθ plus tanθ end fraction cross times fraction numerator secθ minus tanθ over denominator secθ minus tanθ end fraction close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space secθ minus open parentheses fraction numerator secθ minus tanθ over denominator sec squared straight theta minus tan squared straight theta end fraction close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space secθ space minus left parenthesis secθ minus tanθ right parenthesis space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space secθ minus secθ plus tanθ space space space space space space space space space space space space space space space space space space space space space space space space space space space space space equals space tanθ
    Hence, L.H.S. = R.H.S.
    Question 385
    CBSEENMA10008278
    Wired Faculty App

    Prove the following identity:
    left parenthesis secθ minus cosecθ right parenthesis space left parenthesis 1 plus tanθ plus cotθ right parenthesis space equals space secθ. space tanθ space minus space cosecθ. space cotθ
    Solution
    straight L. straight H. straight S. space equals space left parenthesis secθ minus cosecθ right parenthesis space left parenthesis 1 plus tanθ plus space cotθ right parenthesis equals space open parentheses 1 over cosθ minus 1 over sinθ close parentheses space open parentheses 1 plus sinθ over cosθ plus cosθ over sinθ close parentheses equals space open parentheses fraction numerator sinθ minus cosθ over denominator cosθ. space sinθ end fraction close parentheses space open parentheses fraction numerator sinθ. space cosθ space plus sin squared straight theta plus cos squared straight theta over denominator cosθ. space sinθ end fraction close parentheses equals space fraction numerator sin cubed straight theta minus cos cubed straight theta over denominator sin squared straight theta. space cos squared straight theta end fraction equals space fraction numerator sin cubed straight theta over denominator sin squared straight theta. space cos squared straight theta end fraction minus fraction numerator cos cubed straight theta over denominator sin squared straight theta. space cos squared straight theta end fraction equals space fraction numerator sin space straight theta over denominator cos squared straight theta end fraction minus fraction numerator cosθ over denominator sin squared straight theta end fraction equals space fraction numerator sin space straight theta over denominator cos space straight theta end fraction cross times fraction numerator 1 over denominator cos space straight theta end fraction minus fraction numerator cos space straight theta over denominator sin space straight theta end fraction cross times fraction numerator 1 over denominator sin space straight theta end fraction equals space tanθ. space secθ space minus space cot space straight theta. space cosec space straight theta equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
    Question 386
    CBSEENMA10008279
    Wired Faculty App

    Prove the following identity:
    fraction numerator tanθ plus secθ minus 1 over denominator tanθ minus secθ plus 1 end fraction equals fraction numerator 1 plus sinθ over denominator cosθ end fraction
    Solution
    straight L. straight H. straight S. space equals space fraction numerator tan space straight theta space plus sec space straight theta space minus 1 over denominator tanθ minus secθ plus 1 end fraction space space space space space space space space space space space space space space equals space fraction numerator left parenthesis tanθ plus secθ right parenthesis space minus space left parenthesis sec squared straight theta minus tan squared straight theta right parenthesis over denominator tanθ minus secθ plus 1 end fraction space space space space space space space space space space space space space space space equals space fraction numerator left parenthesis tanθ plus secθ right parenthesis minus left parenthesis secθ plus tanθ right parenthesis space left parenthesis secθ minus tanθ right parenthesis over denominator tanθ minus secθ plus 1 end fraction space space space space space space space space space space space space space space space space equals space fraction numerator left parenthesis tanθ plus secθ right parenthesis space left square bracket 1 minus left parenthesis secθ plus tanθ right parenthesis over denominator tanθ minus secθ plus 1 end fraction space space space space space space space space space space space space space space space space space space equals space fraction numerator left parenthesis tanθ plus secθ right parenthesis thin space left parenthesis 1 minus secθ plus tanθ right parenthesis over denominator tanθ minus secθ plus 1 end fraction space space space space space space space space space space space space space space space space space space equals space tanθ plus secθ space space space space space space space space space space space space space space space space space space equals space sinθ over cosθ plus 1 over cosθ space space space space space space space space space space space space space space space space space space equals space fraction numerator sinθ plus 1 over denominator cosθ end fraction space equals space straight R. straight H. straight S. space
    Hence, L.H.S. = R.H.S.
    Question 387
    CBSEENMA10008280
    Wired Faculty App

    Prove the following identity:
    fraction numerator cosA over denominator 1 minus tanA end fraction minus fraction numerator sin squared straight A over denominator cosA minus sinA end fraction equals sinA plus cosA.
    Solution
    fraction numerator cosA over denominator 1 minus tanA end fraction minus fraction numerator sin squared straight A over denominator cosA minus sinA end fraction equals sinA plus cosA

    Hence, L.H.S. = R.H.S.
    Question 388
    CBSEENMA10008281
    Wired Faculty App

    Prove the following identity:
    sec A (1 - sin A) (sec A + tan A) = 1
    Solution

    sec A (1 - sin A) (sec A + tan A) = 1
    L.H.S. = sec A (1 - sin A) (sec A + tan A) 
    equals space open parentheses fraction numerator 1 minus sinA over denominator cosA end fraction close parentheses open parentheses 1 over cosA plus sinA over cosA close parentheses equals open parentheses fraction numerator 1 minus sinA over denominator cosA end fraction close parentheses space open parentheses fraction numerator 1 plus sinA over denominator cosA end fraction close parentheses equals space fraction numerator left parenthesis 1 minus sinA right parenthesis thin space left parenthesis 1 plus sinA right parenthesis over denominator cos squared straight A end fraction equals space fraction numerator 1 minus sin squared straight A over denominator cos squared straight A end fraction space equals space fraction numerator cos squared straight A over denominator cos squared straight A end fraction equals space space 1 equals straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.

    Question 389
    CBSEENMA10008282
    Wired Faculty App

    Prove the following identity:
    fraction numerator 1 over denominator secθ minus 1 end fraction plus fraction numerator 1 over denominator secθ plus 1 end fraction equals 2 space cosecθ. space cotθ.
    Solution

    Hence, L.H.S. = R.H.S.
    Question 390
    CBSEENMA10008283
    Wired Faculty App

    Prove the following identity:
    fraction numerator cosecθ plus cotθ over denominator cosecθ minus cotθ end fraction space equals space 1 plus 2 cot squared straight theta plus 2 cosecθ. space cotθ
    Solution
    straight L. straight H. straight S. space equals space fraction numerator cosecθ plus cotθ over denominator cosecθ minus cotθ end fraction space space space space space space space space space space space space space equals space fraction numerator cosecθ plus cotθ over denominator cosecθ minus cotθ end fraction cross times fraction numerator cosecθ plus cotθ over denominator cosecθ plus cotθ end fraction space space space space space space space space space space space space equals space fraction numerator left parenthesis cosecθ plus cotθ right parenthesis thin space left parenthesis cosecθ plus cotθ right parenthesis over denominator cosec squared straight theta minus cot squared straight theta end fraction space space space space space space space space space space space space equals space left parenthesis cosecθ plus cotθ right parenthesis squared space space space space space space space space space space space space equals space cosec squared straight theta plus cot squared straight theta plus 2 space cosecθ. space cotθ space space space space space space space space space space space space equals cot squared straight theta plus 1 plus cot squared straight theta plus 2 space cosecθ. space cotθ space space space space space space space space space space space space equals space 1 plus 2 cot squared straight theta plus 2 cosecθ. space cotθ space space space space space space space space space space space space space equals straight R. straight H. straight S.
    L.H.S.= R.H.S.
    Question 391
    CBSEENMA10008284
    Wired Faculty App

    Prove the following identity:
    fraction numerator cosecθ over denominator cosecθ minus 1 end fraction plus fraction numerator cosecθ over denominator cosecθ plus 1 end fraction equals 2 plus 2 tan squared straight theta.
    Solution
    straight L. straight H. straight S. space equals fraction numerator cosecθ over denominator cosecθ minus 1 end fraction plus fraction numerator cosec space straight theta over denominator cosecθ plus 1 end fraction equals space fraction numerator cosecθ left parenthesis cosecθ plus 1 right parenthesis plus cosecθ left parenthesis cosecθ minus 1 right parenthesis over denominator left parenthesis cosecθ minus 1 right parenthesis thin space left parenthesis cosecθ plus 1 right parenthesis end fraction equals space fraction numerator cosec squared straight theta plus cosecθ plus cosec squared straight theta minus cosecθ over denominator cosec squared straight theta minus 1 end fraction equals space fraction numerator 2 space cosec squared straight theta over denominator cot squared straight theta end fraction space equals space fraction numerator 2 over denominator cot squared straight theta end fraction cosec squared straight theta equals 2 space tan squared straight theta space left parenthesis cot squared straight theta plus 1 right parenthesis equals space 2 space tan squared straight theta. space cot squared straight theta plus 2 space tan squared straight theta space equals space 2 plus 2 space tan squared straight theta equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
    Question 392
    CBSEENMA10008285
    Wired Faculty App

    Prove the following identity:
    square root of fraction numerator 1 plus cosθ over denominator 1 minus cosθ end fraction end root equals space cosecθ plus cotθ.
    Solution
    straight L. straight H. straight S. space equals space square root of fraction numerator 1 plus cosθ over denominator 1 minus cosθ end fraction end root space space space space space space space space space space space space space space equals square root of fraction numerator 1 plus cosθ over denominator 1 minus cosθ end fraction cross times fraction numerator 1 plus cosθ over denominator 1 plus cosθ end fraction end root space space space space space space space space space space space space space equals space square root of fraction numerator left parenthesis 1 plus cosθ right parenthesis squared over denominator 1 minus cos squared straight theta end fraction end root space equals space square root of fraction numerator left parenthesis 1 plus cosθ right parenthesis squared over denominator sin squared straight theta end fraction end root space space space space space space space space space space space space space equals space square root of open parentheses fraction numerator 1 plus cosθ over denominator sinθ end fraction close parentheses squared end root space equals space open parentheses fraction numerator 1 plus cosθ over denominator sin space straight theta end fraction close parentheses space space space space space space space space space space space space space space equals space 1 over sinθ plus cosθ over sinθ space equals space cosecθ plus cotθ space space space space space space space space space space space space space space equals space straight R. straight H. straight S.
    Question 393
    CBSEENMA10008286
    Wired Faculty App

    Prove the following identity:
    fraction numerator tanθ over denominator 1 minus cotθ end fraction plus fraction numerator cotθ over denominator 1 minus tanθ end fraction equals 1 plus tanθ plus cotθ.
    Solution
    straight L. straight H. straight S. space equals space fraction numerator tanθ over denominator 1 minus cotθ end fraction plus fraction numerator cot space straight theta over denominator 1 minus tanθ end fraction equals space fraction numerator begin display style fraction numerator sin space straight theta over denominator cos space straight theta end fraction end style over denominator 1 minus begin display style fraction numerator cos space straight theta over denominator sin space straight theta end fraction end style end fraction plus fraction numerator begin display style fraction numerator cos space straight theta over denominator sin space straight theta end fraction end style over denominator 1 minus begin display style fraction numerator sin space straight theta over denominator cos space straight theta end fraction end style end fraction equals space fraction numerator begin display style fraction numerator sin space straight theta over denominator cos space straight theta end fraction end style over denominator begin display style fraction numerator space sinθ minus cosθ over denominator sinθ end fraction end style end fraction plus fraction numerator begin display style cosθ over sinθ end style over denominator begin display style fraction numerator cos space straight theta space minus space sin space straight theta over denominator cos space straight theta end fraction end style end fraction equals space fraction numerator sin space straight theta over denominator cos space straight theta end fraction cross times space fraction numerator sin space straight theta over denominator sin space straight theta minus cos space straight theta end fraction plus fraction numerator cos space straight theta over denominator sin space straight theta end fraction cross times fraction numerator cos space straight theta over denominator cos space straight theta minus sin space straight theta end fraction
    equals space fraction numerator sin squared straight theta over denominator cos space straight theta left parenthesis sinθ minus cosθ right parenthesis end fraction plus fraction numerator cos squared straight theta over denominator sin space straight theta space left parenthesis cosθ minus sinθ right parenthesis end fraction equals space fraction numerator sin squared straight theta over denominator cosθ left parenthesis sinθ minus cosθ right parenthesis end fraction plus fraction numerator cos squared straight theta over denominator sinθ left parenthesis cosθ minus sinθ right parenthesis end fraction equals space fraction numerator sin squared straight theta over denominator cosθ left parenthesis sinθ minus cosθ right parenthesis end fraction minus fraction numerator cos squared straight theta over denominator sinθ left parenthesis sinθ minus cosθ right parenthesis end fraction equals space fraction numerator sin cubed straight theta minus cos cubed straight theta over denominator cosθ. space sinθ space left parenthesis sinθ minus cosθ right parenthesis end fraction equals space fraction numerator left parenthesis sinθ space minus space cosθ right parenthesis thin space left parenthesis sin squared straight theta plus cos squared straight theta plus sinθ. space cosθ right parenthesis over denominator sinθ. space cosθ space left parenthesis sinθ minus cosθ right parenthesis end fraction equals space fraction numerator sin squared straight theta plus cos squared straight theta plus sinθ. space cosθ over denominator sinθ. space cosθ end fraction equals space fraction numerator sin squared straight theta over denominator sin space straight theta. space cosθ end fraction plus fraction numerator cos squared straight theta over denominator sinθ. space cosθ end fraction plus fraction numerator sinθ. space cosθ over denominator sinθ. space cosθ end fraction equals space sinθ over cosθ plus cosθ over sinθ plus 1 equals space tanθ plus cotθ plus 1 equals space straight R. straight H. straight S.
    Hence, L.H.S. = R.H.S.
    Question 394
    CBSEENMA10009645
    Wired Faculty App

    The ratio of the height of a tower and the length of its shadow on the ground is √3:1. What is the angle of elevation of the sun?
    Solution

    Let the height of the tower be x and y the length of the shadow on the ground be x:y.

    The angle of elevation of the sun from the ground is θ.
    We have, x:y =√3:1
    Now, In ∆ABC
    tan space straight theta space equals fraction numerator space Height space over denominator Base end fraction tan space straight theta space equals space AB over BC space tan space straight theta space equals fraction numerator square root of 3 over denominator 1 end fraction therefore space tan space straight theta space space equals space 60 degree

    Question 395
    CBSEENMA10009664
    Wired Faculty App

    A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
    Solution
    Let the distance BC be x m and CD be y m. 

    In ∆ABC,
    tan space 60 degree space equals space AB over BC space equals space 150 over straight x rightwards double arrow space square root of 3 space equals space 150 over straight x rightwards double arrow space straight x space equals space fraction numerator 150 space straight m over denominator square root of 3 end fraction.... space left parenthesis straight i right parenthesis
    In ∆ABD,
    tan space 45 degree space equals space AB over BD space equals space fraction numerator 150 over denominator straight x plus straight y end fraction rightwards double arrow space 1 space equals space fraction numerator 150 over denominator straight x plus straight y end fraction rightwards double arrow straight x space plus straight y space equals space 150 rightwards double arrow space straight y space equals space 150 minus straight x
    Using (1), we get
    rightwards double arrow space straight y space equals space 150 space minus fraction numerator 150 over denominator square root of 3 end fraction space equals space fraction numerator 150 left parenthesis square root of 3 minus 1 right parenthesis over denominator square root of 3 end fraction space straight m
    Time taken to move from point C to point D is 2 min = 2/60 h=1/30 h.
    Now,
    Speed space equals space Distance over Time space equals space fraction numerator straight y over denominator 1 divided by 30 end fraction space equals space fraction numerator begin display style fraction numerator 150 left parenthesis square root of 3 minus 1 right parenthesis end root over denominator square root of 3 end fraction end style over denominator 1 divided by 30 end fraction space equals space 1500 square root of 3 left parenthesis square root of 3 minus 1 right parenthesis straight m divided by straight h
    Question 396
    CBSEENMA10009674
    Wired Faculty App

    The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow in water of lake is 60°. Find the height of the cloud from the surface of the water. 
    Solution

    Let AB be the surface of the lake and P be the point of observation such that AP = 60 m. Let C be the position of the cloud and C be its reflection in the lake.
    Then CB =
    Draw PM⊥CB
    Let CM = h
    ∴ CB = h + 60 m

    In ∆CPM
    tan 30 to the power of straight o space equals space CM over PM rightwards double arrow space fraction numerator 1 over denominator square root of 3 end fraction space equals space straight h over PM rightwards double arrow space PM space equals space square root of 3 straight h space space.... space left parenthesis straight i right parenthesis In increment PMC comma tan 60 to the power of straight o space equals space fraction numerator straight C apostrophe straight M over denominator PM end fraction rightwards double arrow space tan 60 to the power of 0 space equals space fraction numerator straight C apostrophe straight B space plus BM over denominator PM end fraction rightwards double arrow space square root of 3 space equals space fraction numerator straight h space plus 60 space straight m space plus 60 space straight m over denominator PM end fraction rightwards double arrow space PM space equals space fraction numerator straight h space plus 120 over denominator square root of 3 end fraction space... space left parenthesis ii right parenthesis From space equ space left parenthesis straight i right parenthesis space and space left parenthesis ii right parenthesis square root of 3 straight h space equals fraction numerator straight h space plus 120 space straight m over denominator square root of 3 end fraction space

    ⇒ 3h = h + 120 m
    ⇒ 2h = 120 m
    ⇒ h = 60 m
    CB = h + 60m = 60m + 60m = 120m
    Thus, the height of the cloud from the surface of the lake is 120 m.

    Question 397
    CBSEENMA10009703
    Wired Faculty App

    As observed from the top of a 100 m high light house from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the light house, find the distance between the two ships. [Use √3= 1.732]
    Solution

    Let ships are at distance x from each other,

    In ∆ APOtan 45o = 100y = 1∴ y = 100 m ..... (i)In ∆POBtan 30° = OPOB = 100x +y = 133 = x + y100x + y = 1003x = 1003 - y = 1003 - 100 100(3 -1)∴ x = 100 (1.732 -1 )= 100 x 0.732= 73.2 m

    Question 398
    CBSEENMA10009714
    Wired Faculty App

    The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30o. The distance of the car from the base of the tower (in m.) is

    • 253

    • 503

    • 753

    • 150
    Solution

    C.

    753

    Let AB be the tower of height 75 m and C be position of the car.

    In 

    ∆ABC,cot 30°= ACAB⇒AC=AB cot 30°⇒AC=75m x 3⇒AC=753mThus, the distance of the car from the base of the tower is 753 m. 

    Question 399
    CBSEENMA10009742
    Wired Faculty App

    The horizontal distance between two poles is 15 m. The angle of depressionof the top of first pole as seen from the top of second pole is 30o. If theheight of the second pole is 24 m, find the height of the first pole.   Use 3 = 1.732
    Solution

     Let Ab and CD be the two poles, where CD (the second  pole ) = 24 m.BD = 15 mLet the height of pole AB be h  mAl=BD= 15 m  and  AB= LD = h So,  CL= CD - LD = 24-hIn ∆ACL,tan 30° = CLAL ⇒tan 30° = 24-h15 ⇒13 = 24-h15⇒24-h = 153 = 53⇒h= 24-53⇒h=24-5 x 1.732          Taking 3  = 1.732⇒h=15.34Thus, height of the first pole is 15.34 m. 

    Question 400
    CBSEENMA10009747
    Wired Faculty App

    Two poles of equal heights are standing opposite each other on either sideof the roads, which is 80 m wide. From a point between them on theroad, the angles of elevation of the top of the poles are 60o and 30orespectively. Find the height of the poles and the distances of the pointfrom the poles.
    Solution

    Let  AC and  BD  be the two poles of the same height  h m.Given: AB = 80 mLet AP = x m, therefore, PB = (80 - x ) mIn ∆APC,tan 30° = ACAP13 = hx        .........(1)In ∆BPD,tan 60° = BDAB3 =h80-x       .............(2)Dividing (1) by (2),133 = hx  h80-x⇒13 = 80-xx⇒x = 240 - 3x⇒ 4x = 240⇒ x = 60From (1),13 = hx⇒h = 603 = 203 mThus, the height of both the poles is  203 m and the distance of the point fromthe poles are  60 m and  20 m.

     

    Question 401
    CBSEENMA10009770
    Wired Faculty App

    The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [Use 3 = 1.73 ]
    Solution

    Let AB is the tower of height h meter and AC is flagstaff of height x meter.

                             

     

    ∠APB = 45° and ∠BPC = 60°Tan60 = x + h120   3  =  x + h120 x + h = 1203          x =  1203 - h  Tan 45 = h120           1 = h120           h = 120Therefore height of the flagstaff = 1203 - 120                                                  = 120 ( 3 -1 ) m                                                  = 120 ( 1.73 - 1 ) m                                                  = 120 x 0.73 m                                                  = 87.6 m

    Question 402
    CBSEENMA10009777
    Wired Faculty App

    The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is

    • 503

    • 1503

    • 1502

    • 75
    Solution

    A.

    503

                          

    Let AB be the tower and BC be the distance between tower and car. Let θ be the angle of depression of the car.

    According to the given information,

    In ∆ABC,tanθ = BCAB       Using (1) and tan30° = 13∴BC = 1503 = 15033 = 503Hence, distance between the tower and car is  503 .

    Question 403
    CBSEENMA10009780
    Wired Faculty App

    If a tower 30 m high, casts a shadow 10 3m long on the ground, then what is the angle of elevation of the sun?
    Solution

                            

    Let AB be the tower and BC  be its shadow.

    AB = 30 m, BC = 103 mIn ∆ABC,tanθ = ABBC⇒tanθ = 30103 ⇒tanθ =33tan θ = 3  But, tan 60° =3 ∴ θ = 60°Thus, the angle of elevation of sun is 60°. 

    Question 404
    CBSEENMA10009789
    Wired Faculty App

    On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
    Solution

                           

    Let AB be the tower with height h.

    Let x be the angle of elevation from c.

    So, the angle of elevation from D is (90-x).

               ..........( Since the angle of elevation from C and D are complementary)

    In ∆CAB,tan x = ABAC⇒tanx = h4      .........(i)In ∆DAB,tan(90-x) = ABAD⇒tan(90-x) = h16⇒cot x = 16h    ...........(ii)From (i) and (ii) ,tan x  ×  cot x = h4 x h16⇒1 = h264⇒h2 = 64⇒h = 64⇒h = 8 mHence, the height of the tower is 8 m.

    Question 405
    CBSEENMA10009807
    Wired Faculty App

    From the top of a tower, 100 m high, a man observe two cars on the opposite sides of the tower and in same straight line with its base, with its base, with angles of depression 30° and 45°. Find the distance between the cars.
    [Take 3 = 1.732]
    Solution

              

    The man is at the top of the tower AB.

    In right angled triangle ∆ABX  and  ∆ABY,

     

    tan 45° = ABXB ⇒    1 = 100XB  ⇒ XB = 100 m.tan 30° = ABYB ⇒13 = 100YB ⇒ YB = 1003XY = XB + YB = 100 + 1003                           = 100 + 100 X 1.732                          = 100 + 173.20                          = 200.20   (approx) 

    Hence, the distance between X and Y is 273.20 m approximately.

    Question 406
    CBSEENMA10009809
    Wired Faculty App

    The length of shadow of a tower on the plane ground is 3 times the height of the tower. The angle of elevation of sun is

    • 450

    • 300

    • 600

    • 900
    Solution

    B.

    300

                     

    Let AB be the tower and BC be its shadow. Let θ be the angle of elevation of the sun.

    According to the given information,

    BC = 3 AB     ..........(1)In ∆ABC,tanθ = ABBC = AB3 AB = 13     [Using (1)]We know that tan 300 = 13∴ θ = 300 

    Hence, the angle of elevation of the sun is 300.

    Question 407
    CBSEENMA10009831
    Wired Faculty App

    A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60o. Find the length of the string assuming
    that there is slack in the string.
    Solution

                               

    Given: Position of kite is B.

    Height of kite above ground is = 45 m.

    Angle of inclination is = 600

    Required length of string is = AB.

    In right angled triangle AOB,

     

    SinA = OBAB ⇒ Sin60° = 45AB⇒ 32 = 45AB⇒AB = 45 X 23⇒ AB = 903⇒ AB = 90 X 33 X 3 = 90 X 33⇒ AB = 303 m.

     

    Question 408
    CBSEENMA10009836
    Wired Faculty App

    The angle of elevation of the top of a hill at the foot of a tower is 600 and the angle of depression from the top of the tower of the foot of the hill is 300. If the tower is 50 m high, find the height of the hill.
    Solution

                               

    Let the height of hill is  h.

    In right triangle ABC,

    50AB = tan300 ⇒50AB = 13⇒ AB = 503In right triangle ABD,hAB = tan600 ⇒ hAB = 3⇒ h = 3 AB⇒ h = 3 503 = 150 m.

    Hence the height of hill is 150 m.

    Mock Test Series

    Sponsor Area

    Sponsor Area

    NCERT Book Store

    NCERT Sample Papers

    Entrance Exams Preparation