Some Applications of Trigonometry

Name: Wired Faculty - The Best Learning App
Rating: 4.6 (1864 reviews)

Question

If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Solution

Let us consider two right angle triangles right angled at Q and S respectively.
Now,

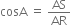
cosA space equals space AS over AR

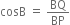
cosB space equals space BQ over BP

But cos A = cos B (given)
∴

AS over AR equals BQ over BP

rightwards double arrow

AS over BQ space equals space AR over BP

Let

AS over BQ equals AR over BP equals straight K

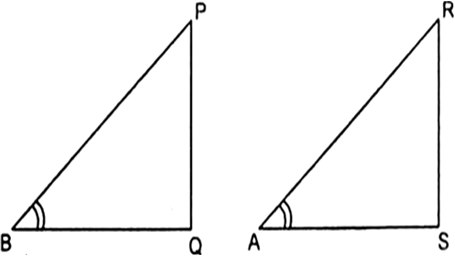
In ΔRAS,
Using Pythagoras theorem, we have

RS space equals space square root of AR squared minus AS squared end root space space space space space space space equals space square root of left parenthesis straight K times BP right parenthesis squared minus left parenthesis straight K. BQ right parenthesis squared end root space space space space space space space space equals space square root of left parenthesis straight K squared times BP squared minus straight K squared times BQ right parenthesis squared end root space space space space space space space equals space square root of straight K squared left parenthesis BP squared minus BQ squared right parenthesis end root space space space space space space equals space straight K square root of left parenthesis BP squared minus BQ squared right parenthesis end root

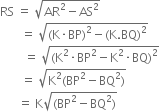
In APBQ,
Using Pythagoras theorem, we have

PQ space equals space square root of BP squared minus BQ squared end root

So,

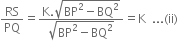
RS over PQ equals fraction numerator straight K. square root of BP squared minus BQ squared end root over denominator square root of BP squared minus BQ squared end root end fraction equals straight K space space... left parenthesis ii right parenthesis

Comparing (i) and (ii), we get

<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

So, by using SSS similar condition

space increment RSA space tilde space increment PQB

∴

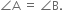
angle straight A space equals space angle straight B.

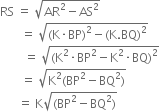
For Daily Free Study Material Join wiredfaculty

Some Applications Of Trigonometry

If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Some More Questions From Some Applications of Trigonometry Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction