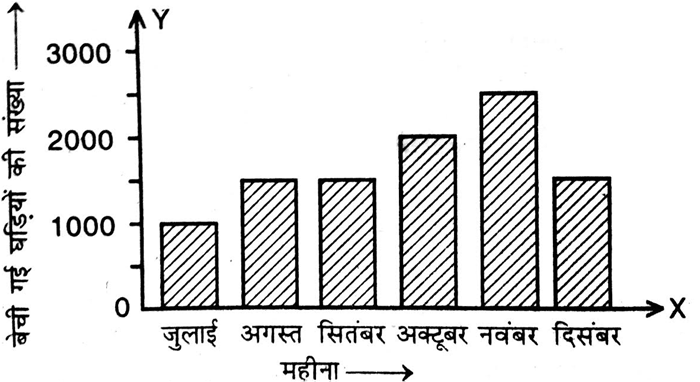
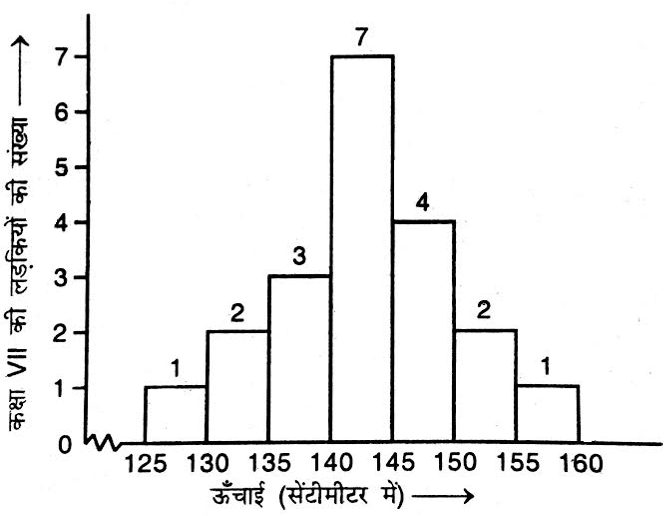
दी हुई सूचना को निरूपित करने के लिए एक उपयुक्त आलेख खींचिए।
| महीना | जुलाई | अगस्त | सितंबर | अक्टूबर | नवंबर | दिसंबर |
| बेची गई घड़ियों की संख्या | 1000 | 1500 | 1500 | 2000 | 2500 | 1500 |
दंड आलेख पर दिए आँकड़ों को निरूपित करने के लिए x-अक्ष पर महीना और y-अक्ष पर बेची गई घड़ियों की संख्या को दर्शाएंगे। क्योंकि हमे 6 गणितीय आँकड़े दिए गए हैं, अत: हम क्षैतिज रेखा पर समान दूरी पर 6 बिंदु लगाएंगे और इन बिंदुओं पर समान मोटाई के आयत खींचेगे।