☰
✕

समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
Question
Wired Faculty App

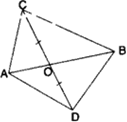
आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखण्ड CD रेखाखण्ड
AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि:
ar(AABC) = ar(ΔABD).है।

Answer

ज्ञात है: ΔABC और ΔABD एक ही आधार पर स्थित है। रेखाखण्ड AB से समद्विभाजित करती है अर्थात् OC = OD
सिद्ध करना है: ar(ΔABC) = ar(ΔABD).
प्रमाण:  ΔACD में  OA एक माध्यिका है।
∴     ar(OAC) = ar(OAD)           ...(i)
इसी प्रकार, ΔBCD में, OB एक माध्यिका है।
∴   ar(OBC) = ar(OBD)          ...(ii) 
(i) और (ii) से
ar(OAC) + ar(OBC) = ar(OAD) + ar(OBD)
अत: ar(ABC) = ar(ABD)
 

 

Sponsor Area

Some More Questions From समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Chapter

आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखण्ड CD रेखाखण्ड
AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि:
ar(AABC) = ar(ΔABD).है।

बिंदु D और E क्रमश: ΔABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि 
ar(ΔDBC) = ar(ΔEBC) है। दर्शाइए  कि DE || BC है।

आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समान्तर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि: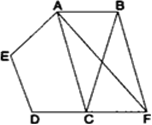
 

(i)  ar(ΔACB) = ar(ΔACF)
(ii) ar(AEDF) = ar(ABCDE)