☰
Triangles
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
Circumcentre of a triangle is always equidistant from all the vertices of that triangle. Circumcentre is the point where perpendicular bisectors of all the sides of the triangle meet together.
In ΔABC, we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle. O is the point where these bisectors are meeting together. Therefore, O is the point which is equidistant from all the vertices of ΔABC.
Sponsor Area
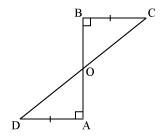
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
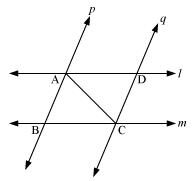
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.
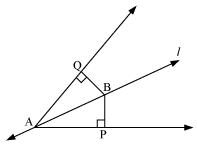
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
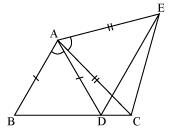
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE
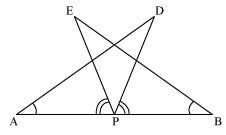
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
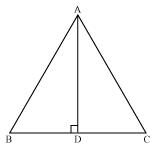
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
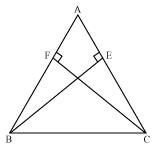
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
Sponsor Area
Sponsor Area