In a huge park people are concentrated at three points (see the given figure)

A: where there are different slides and swings for children,

B: near which a man-made lake is situated,

C: which is near to a large parking and exit.

Where should an ice-cream parlour be set up so that maximum number of persons can approach it?

(Hint: The parlor should be equidistant from A, B and C)

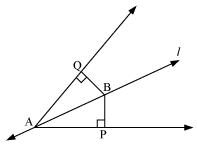
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:

(i) ΔAPB ≅ ΔAQB

(ii) BP = BQ or B is equidistant from the arms of ∠A.

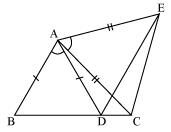
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

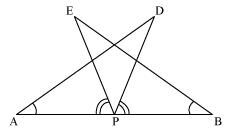
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that

(i) ΔDAP ≅ ΔEBP

(ii) AD = BE

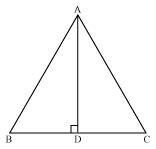
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.

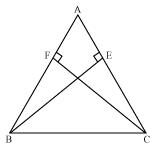
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.

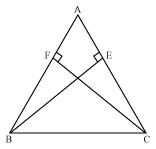
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that

(i) ΔABE ≅ ΔACF

(ii) AB = AC, i.e., ABC is an isosceles triangle.

ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.

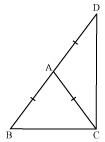
ABC is a right angled triangle in which ∠A = 90º and AB = AC. Find ∠B and ∠C.