☰
Triangles
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.
Let us join AC. In ΔABC, AB < BC (AB is the smallest side of quadrilateral ABCD) ∴ ∠2 < ∠1 (Angle opposite to the smaller side is smaller) … (1) In ΔADC, AD < CD (CD is the largest side of quadrilateral ABCD) ∴ ∠4 < ∠3 (Angle opposite to the smaller side is smaller) … (2) On adding equations (1) and (2), we obtain ∠2 + ∠4 < ∠1 + ∠3 ⇒ ∠C < ∠A ⇒ ∠A > ∠C Let us join BD.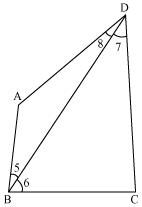
In ΔABD,
AB < AD (AB is the smallest side of quadrilateral ABCD)
∴ ∠8 < ∠5 (Angle opposite to the smaller side is smaller) … (3)
In ΔBDC,
BC < CD (CD is the largest side of quadrilateral ABCD)
∴ ∠7 < ∠6 (Angle opposite to the smaller side is smaller) … (4)
On adding equations (3) and (4), we obtain
∠8 + ∠7 < ∠5 + ∠6
⇒ ∠D < ∠B
⇒ ∠B > ∠D
Sponsor Area
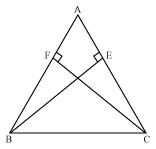
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
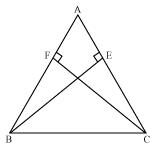
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
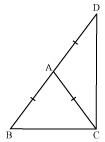
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that ∠BCD is a right angle.
ABC is a right angled triangle in which ∠A = 90º and AB = AC. Find ∠B and ∠C.
Show that the angles of an equilateral triangle are 60º each.
AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠A.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Sponsor Area
Sponsor Area