If g is the inverse of a function f and f'(x) = 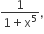 then g'(x) is equal to
then g'(x) is equal to
-
1+ x6
-
5x4
-
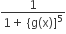
-
1+{g(x)}5
D.
1+{g(x)}5
Here 'g' is the inverse of f(x)
⇒ fog (x) =x
On differentiating w.r.t x, we get
f'{g(x)} x g'(x) =1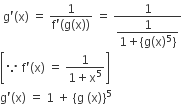
If g is the inverse of a function f and f'(x) = 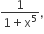 then g'(x) is equal to
then g'(x) is equal to
1+ x6
5x4
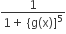
1+{g(x)}5
D.
1+{g(x)}5
Here 'g' is the inverse of f(x)
⇒ fog (x) =x
On differentiating w.r.t x, we get
f'{g(x)} x g'(x) =1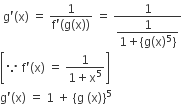
Determine whether each of the following relations are reflexive, symmetric and transitive :
(i) Relation R in the set A = {1, 2, 3,....., 13, 14} defined as
R = {(x, y) : 3 x – y = 0}
(ii) Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4} (iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x,y) : y is divisible by x} (iv) Relation R in the set Z of all integers defined as R = {(x,y) : x – y is an integer}
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y) : x and y work at the same place}
(b) R = {(x,y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R = {(x, y) : x is wife of y}
(e) R = {(x,y) : x is father of y}
Mock Test Series