+91-8076753736[email protected]
logo
logo
-->

Relations And Functions

Question
CBSEENMA12032339
Wired Faculty App

Define binary operation ‘*’ on Q as follows : a * b = a + b – ab, a, b∈ Q
(i) Find the identity element of (Q, *).
(ii) Which elements in (Q. *) are invertible?

Solution

(i) Let e ∈ Q be identifies element of (Q. *)
∴ a * e = a ∀ a ∈ Q ⇒ a + e – ae = a ⇒ (1 – a) e = 0 ⇒ e = 0 as 1 – a ≠ 0 for all a ∈ Q.

Now a * 0 = a + 0 – a. 0 = a and 0 * a = 0 + a – 0 . a = a ∴ a * 0 = 0 * a = a
∴ 0 is the identity element of (Q, *).
(ii) Let a ∈ Q be invertible. Therefore, there exists b ∈ Q such that a * b = 0 ⇒ a + b – ab ⇒ ab – b = a ⇒ (a – 1) b = a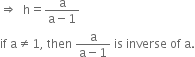
rightwards double arrow space space straight h equals fraction numerator straight a over denominator straight a minus 1 end fraction if space straight a not equal to 1 comma space then space fraction numerator straight a over denominator straight a minus 1 end fraction space is space inverse space of space straight a.
Also 1 ∈ Q has no inverse, for if b is the inverse of 1, then I * b = 0 ⇒ 1 + b – b = 0 ⇒ 1 = 0, which is absurd each element a ∈ Q except a = 1 is invertible.

Some More Questions From Relations and Functions Chapter

Let L be the set of all lines in a plane and R be the relation in L defined as R = {(L1, L2) : L1 is perpendicular to L2}. Show that R is symmetric but neither reflexive nor transitive.

 Determine whether each of the following relations are reflexive, symmetric and transitive :

(i) Relation R in the set A = {1, 2, 3,....., 13, 14} defined as

R = {(x, y) : 3 x – y = 0}

(ii) Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4} (iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x,y) : y is divisible by x} (iv) Relation R in the set Z of all integers defined as R = {(x,y) : x – y is an integer}

(v) Relation R in the set A of human beings in a town at a particular time given by
(a)    R = {(x, y) : x and y work at the same place}
(b)    R = {(x,y) : x and y live in the same locality}
(c)    R = {(x, y) : x is exactly 7 cm taller than y}
(d)    R = {(x, y) : x is wife of y}
(e)    R = {(x,y) : x is father of y}

Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.

Show that the relation R in R defined as R = {(a, b) : a ≤ b}, is reflexive and transitive but not symmetric.

Check whether the relation R in R defined by R = {(a,b) : a ≤ b3} is refleive, symmetric or transitive.

If R and R’ arc reflexive relations on a set then so are R ∪ R’ and R ∩ R’. 

If R and R’ are symmetric relations on a set A, then R ∩ R’ is also a sysmetric relation on A.

Show that the union of two symmetric relations on a set is again a symmetric relation on that set.

Let A = {1. 2. 3}. Then show that the number of relations containing (1,2) and (2. 3) which are reflexive and transitive but not symmetric is four.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation