Explain the process of computing Standard Deviation with the help of an imaginary example.

Standard deviation is the square root of the arithmetic mean of the squares of deviation of the items from their mean value. It is precise measure of dispersion and is denoted by a Greek tetter *** (small sigma).

Computation of Standard Deviation :

Following formula is used to calculate the standard deviation for ungrouped data :

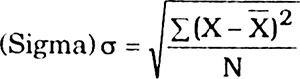
Where σ = Standard deviation (S.D.)

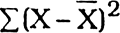= Sum total of squares of deviation

N = Number of items

The above formula becomes rather tedious if the value of X involves decimal points and also if the number of observations is very large. We may then use the following short cut method :

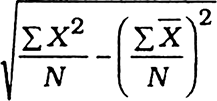
Example : Following table shows the rainfall figures of last ten years. Calculate the standard deviation.