निम्नलिखित प्रत्येक में कितने विकर्ण हैं?
(a) एक उत्तल चतुर्भुज (b) एक समषड्भुज (c) एक त्रिभुज
(a) एक उत्तल चतुर्भुज में भुजाओं की संख्या (n) = 4
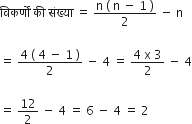
(b) एक समषड्भुज में भिजाओं की संख्या (n) = 6
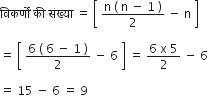
(c) एक त्रिभुज में भुजाओं की संख्या (n) = 3
Sponsor Area
निम्नलिखित प्रत्येक में कितने विकर्ण हैं?
(a) एक उत्तल चतुर्भुज (b) एक समषड्भुज (c) एक त्रिभुज
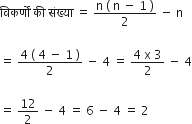
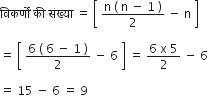
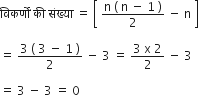
तालिका की जाँच कीजिए: ( प्रत्येक आकृति को त्रिभुजों में बाँटिए और कोणों का योगफल ज्ञात कीजिए )
|
आकृति |
|
|
|
|
|
भुजा |
3 |
4 |
5 |
6 |
|
कोणों का योगफल |
180° |
2 x 180° = (4 - 2) x 180° |
3 x 180° = (5 - 2) x 180° |
4 x 180° = (6 - 2) x 180° |
एक बहुभुज के कोणों के बारे में आप क्या कह सकते हैं जिसकी भुजाओं की संख्या निम्नलिखित हो?
(a) 7 (b) 8 (c) 10 (d) n
Sponsor Area
Sponsor Area
Mock Test Series