Mathematics Chapter 4 Linear Equations In Two Variables
Sponsor Area
NCERT Solution For Class 9 About 2.html
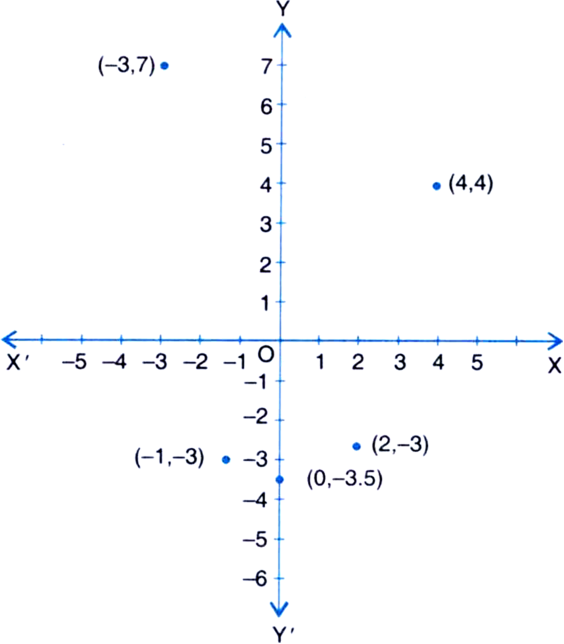
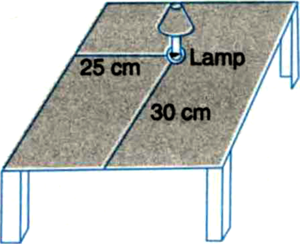
How will you describe the position of a table lamp on your study table to another person?
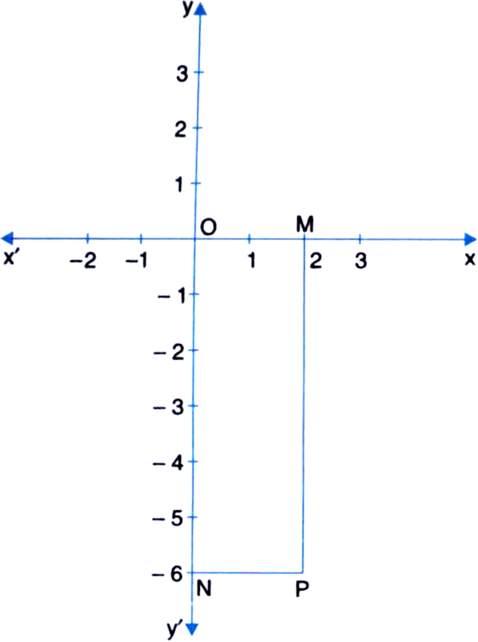
(Street Plan): A city has two main roads which cross each other at the centre of the city.
These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are about 5 streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.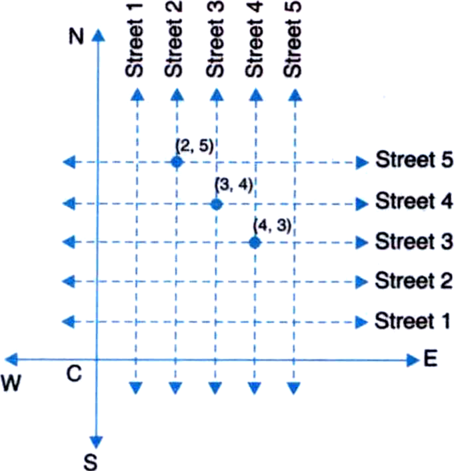
There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross-street is referred to in the following manner: If the 2nd street running in the North-South direction and 5 th in the East-West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
(i) how many cross-streets can be referred to as (4, 3)?
(ii) how many cross-streets can be referred to as (3, 4)?
Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
(i) The x-axis and the y-axis.
(ii) Quadrants.
(iii) The origin.
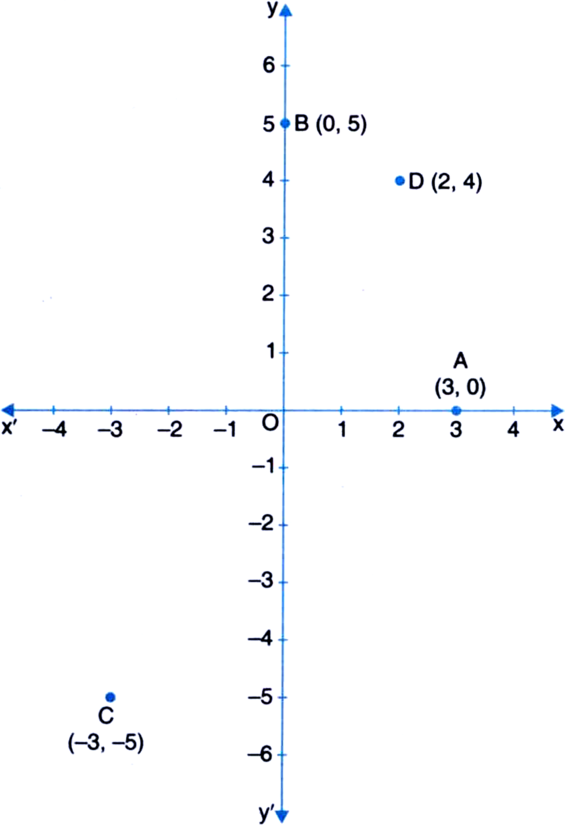
See figure and write the following:
(i) The coordinates of B.
(ii) The coordinates of C.
(iii) The point identified by the coordinates (-3, -5).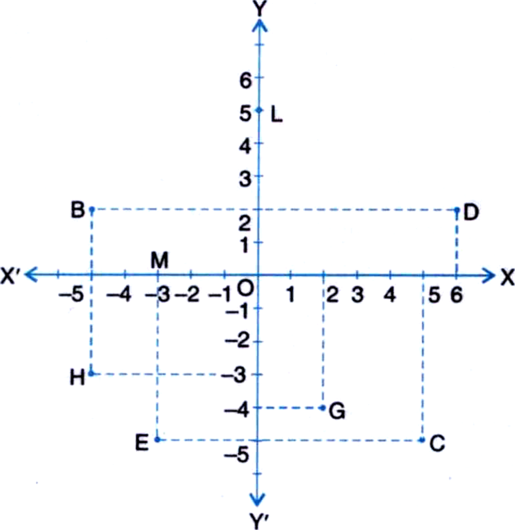
(iv) The point identified by the coordinates (2, - 4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii) The coordinates of the point M.
(i) B → (- 5, 2)
(ii) C → (5, - 5)
(iii) E
(iv) G
(v) 6
(vi) - 3
(vii) L → (0, 5)
(viii) M → (- 3, 0)
See the figure given below and write the following:
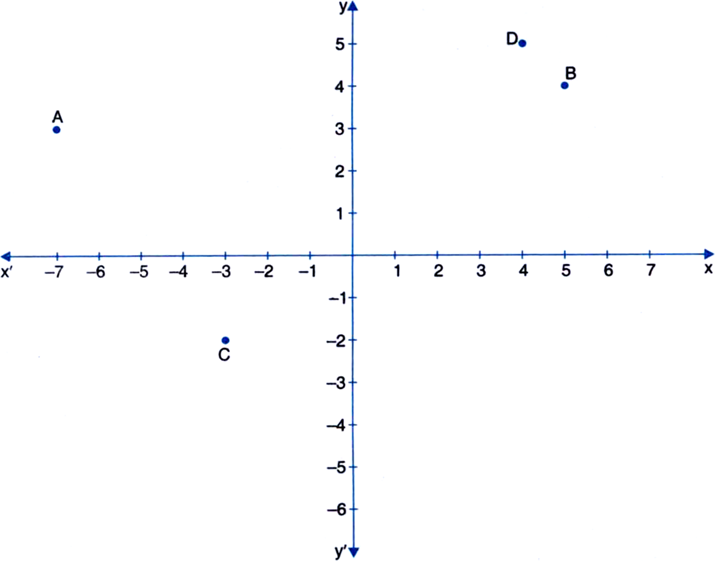
(i) Coordinates of point A
(ii) Abscissa of point D
(iii) The point identified by the co-ordinates (5, 4)
(iv) Co-ordinates of point C
(i) A → (-7, 3)
(ii) D → (4, 5) (iii) B
(iv) (-3, -2)
In figure given below, triangle AOB with coordinates of A and O as (4, 0) and (0, 0), find the coordinates of B.

In right triangle AOB OA2 + OB2 = AB2
| By Pythagoras Theorem
⇒ 42 + OB2 = 52
⇒ 16 + OB2 = 25
⇒ OB2 = 9
⇒ OB = 3
⇒ B → (0, 3)
The perpendicular distance of a point from the x-axis is 2 units and the perpendicular distance from the y-axis is 3 units. Write the coordinates of the point if it lies in the:
(i) I quadrant (ii) II quadrant
(iii) III quadrant (iv) IV quadrant
(i) (3, 2)
(ii) (-3, 2)
(iii) (-3, -2)
(iv) (3, -2)
In figure, ∆ABC and ∆ABD are equilateral triangles. Find the coordinates of points C and D.
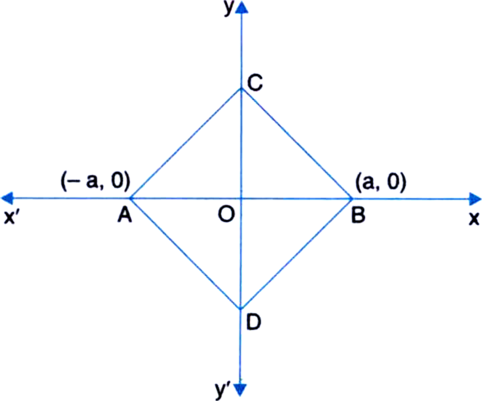
∵ ∆ABC is an equilateral triangle
∴AC = BC = AB
⇒ BC = AB
⇒ BC = 2a
In right triangle COB,
OB2 + OC2 = BC2 ![]() a2 + OC2 = (2a)2
a2 + OC2 = (2a)2![]() OC2 + 3a2
OC2 + 3a2![]()
![]()
![]()
Similarly, ![]()
In figure, ABCD is a square. Find the co-ordinates of points A and D.

A → (-1, 3)
D → (2, -2)
In figure, ∆ABC is an equilateral triangle with co-ordinates of B and C as B (1, 0) and C (5, 0). Find the co-ordiantes of vertex A.

Let D be the middle point of BC. Join AD. Then, ∠BDA = 90°
∵ ∆ABC is an equilateral triangle
∴AB = AC = BC
⇒ AB = BC
⇒ AB = 5 - 1 = 4 = BC BD = 3 - 1 = 2
In right triangle BDA,
AB2 = AD2 + BD2 ![]() (4)2 = AD2 + (2)2
(4)2 = AD2 + (2)2![]() 16 = AD2 + 4
16 = AD2 + 4![]() AD2 = 12
AD2 = 12![]() AD =
AD = ![]()
![]()
In figure, ∆PQR is an equilateral triangle with co-ordinates of vertices Q and R as (-2, 0) and (2, 0). Find the co-ordinates of the vertex P.
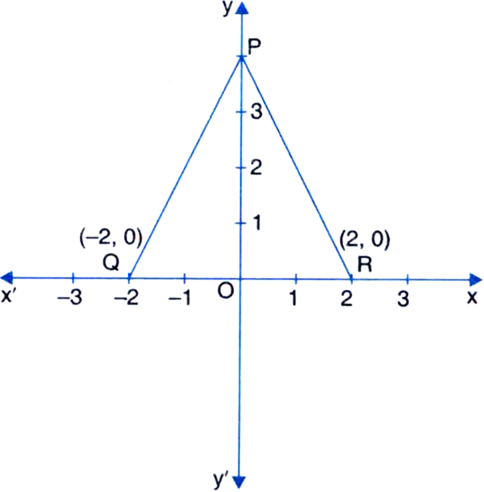
∵ ∆PQR is an equilateral triangle
∴ PQ = PR = QR
⇒ PQ = QR
⇒ PQ = 4
OQ = 2
In right triangle POQ,
OP2 + OQ2 = PQ2 |By Pythagoras Theorem
⇒ OP2 + (2)2 = (4)2![]()
In figure, write the co-ordinates of the points P, Q, R and S.

P → (3, 0)
Q → (0, -4)
R → (-5, 4)
S → (2, -3)
Find the co-ordinates of a point:
(i) whose ordinate is 6 and lies on y-axis.
(ii) whose abscissa is -3 and lies on x-axis.
(i)(0, 6)
(ii) (-3, 0)
In which quadrant, can a point have:
(i) abscissa equal to its ordinate
(ii) ordinate equal in magnitude to abscissa
(iii) ordinate equal and opposite of abscissa
(iv) abscissa twice that of the ordinate.
(i) I, III
(ii) I, II, III, IV
(iii) II, IV
(iv) I, III
See figure and complete the following statements:
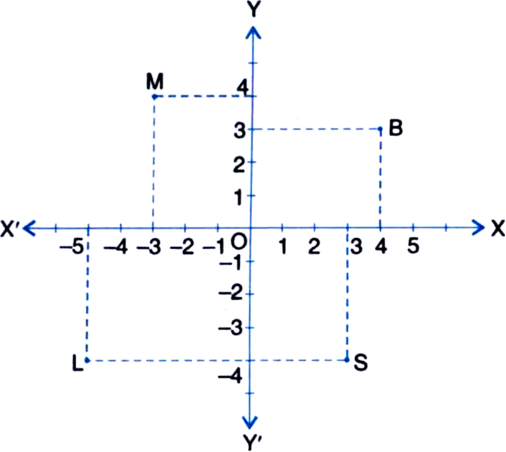
(i) The abscissa and the ordinate of the point B are _ _ _ and _ _ _, respectively. Hence the coordinates of B are (_ _, _ _).
(ii) The x-coordinate and the y-coordinate of the point M are _ _ _ and _ _ _, respectively. Hence the coordinates of M are (_ _ _, _ _ _).
(iii) The x-coordinate and the y-coordinate of the point L are _ _ _ and _ _ _, respectively. Hence the coordinates of L are (_ _, _ _).
(iv) The x-coordinate and the y-coordinate of the point S are _ _ _ and _ _ _, respectively. Hence the coordinates of S are (_ _, _ _).
Solution not provided.
(i) 4, 3 (4, 3)
(ii) -3, 4, (-3, 4)
(iii) -5, -4, (- 5, -4)
(iv) 3, -4, (3, - 4)
Sponsor Area
Write the coordinates of the points marked on the axes in the following figure:

Solution not provided.
Ans. 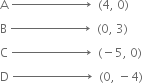
In which quadrant do the given points lie?
(a) (2, -1) (b) (-1, 7)
(c) (-2, -3) (d) (4, 5)
Solution not provided.
Ans. (a) IV (b) II (c) III (d) I
Write the co-ordinates of A, B, C and D from the figure given below:
Solution not provided.
Ans. ![]()
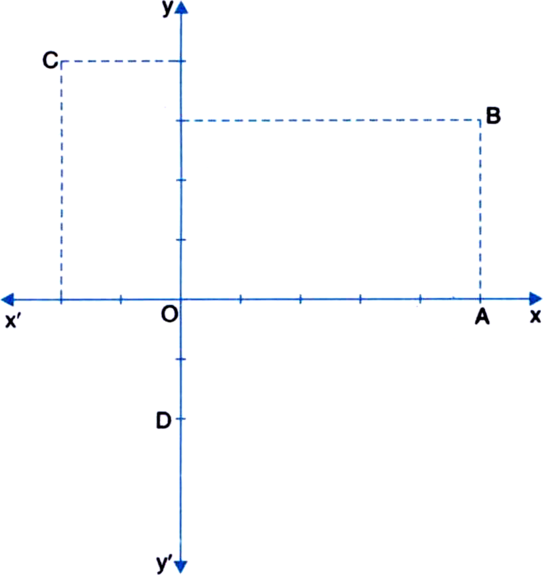
Observe figure and answer the following:
(a) co-ordinates of B
(b) point identified by the coordinates (-2, -3)
(c) abscissa of point D (d) ordinate of point H
(e) points with the same abscissa
(f) points with the same ordinate
Solution not provided.
Ans. (a) (2, 3); (b) A; (c) 0; (d) 0; (e) M, D, H; B, G; (f) M, H
In figure, ∆ABC is an equilateral triangle with coordinates of B and C as (-4, 0) and (4, 0) respectively. Find the coordinates of the vertex.
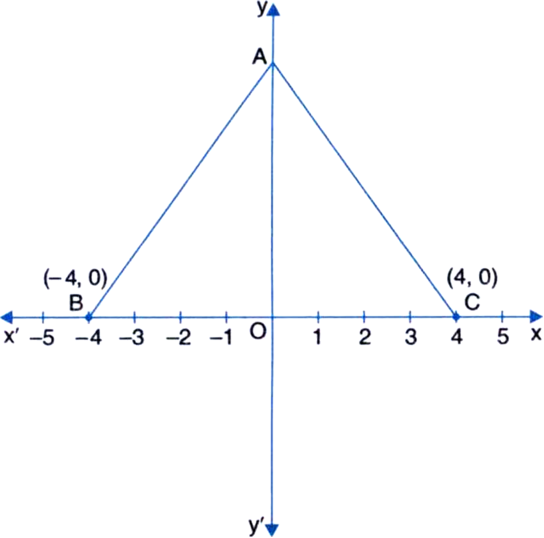
Solution not provided.
Ans. ![]()
In which quadrant do the following points lie?
(a) (-4, -5) (b) (-3, 5)
(c) (2, 2) (d) (4, -1)
Solution not provided.
Ans. (a) III (b) II (c) IV
Find the co-ordinates of the point which lies on y-axis at a distance of 4 units in negative direction of y-axis.
(a) (-4, 0) (b) (4, 0)
(c) (0, -4) (d) (0,4)
Solution not provided.
Ans. C (0, -4)
Plot the points A(-3, -3), B(3, -3), C(3, 3), D(-3, 3) in the cartesian plane. Also, find the length of line segment AB.
Solution not provided.
Ans. 6 Units
The lengths of perpendiculars PM and PN drawn from a point P, on x-axis and y-axis are of 3 and 2 units respectively. Find the coordinates of points P, M and N.
Solution not provided.
Ans. (2, 3) (2, 0), (0, 3)
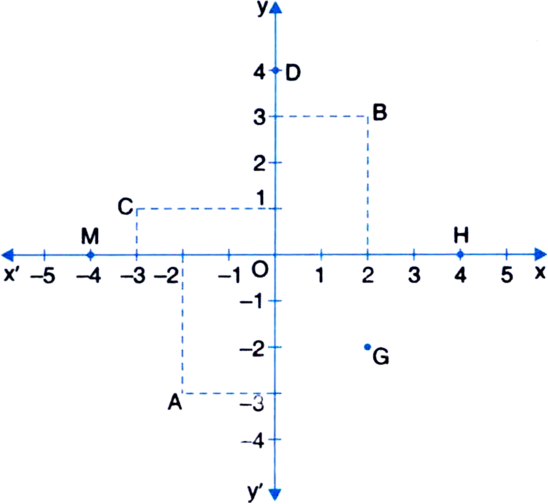
Observe the points plotted in the figure and find the following:
(i) The co-ordinates of E
(ii) The point with the co-ordinates (-4, -1)
(iii) The abscissa of A - abscissa of B
(iv) The ordinate of C + ordinate of F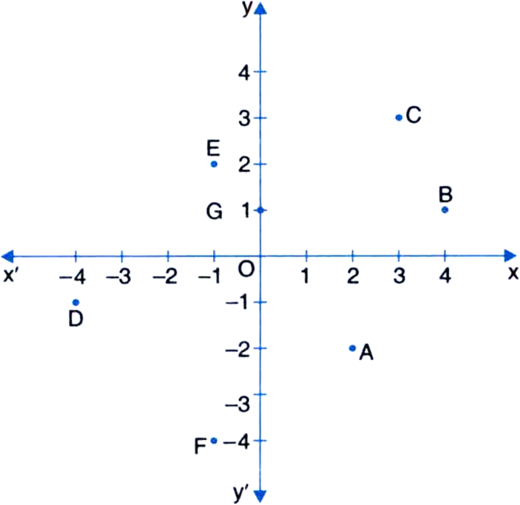
Solution not provided.
Ans. (i) (-1, 2); (ii) D; (iii) - 2; (iv) 4
From given figure write the following:
(a) The coordinates of P
(b) The abscissa of the point Q
(c) The ordinate of the point R
(d) The points whose abscissa is O.
Solution not provided.
Ans. (a) (-3, -2); (b) 0, (c) 0, (d) R, Q, S, T
The perpendicular distance of a point from the x-axis is 4 units and the perpendicular distance from the y-axis is 5 units. Write the co-ordinates of such a point if it lies in the:
(i) I quadrant (ii) II quadrant
(iii) III quadrant (iv) IV quadrant
Solution not provided.
Ans. (i) (5, 4); (ii) (-5, 4); (iii) (-5, -4); (iv) (5, -4)
The perpendicular distance of a point from the x-axis is 2 units and the perpendicular distance from the y-axis is 5 units. Write the co-ordinates of such a point if it lies in the:
(i) I quadrant (ii) II quadrant
(iii) III quadrant (iv) IV quadrant
Solution not provided.
Ans. (i) (5, 2); (ii) (-5, 2); (iii) (-5, -2); (iv) (5, -2)
Find the co-ordinates of the points A, B, C, D, E and F. Which of the points are mirror images in
(i) x-axis (ii) y-axis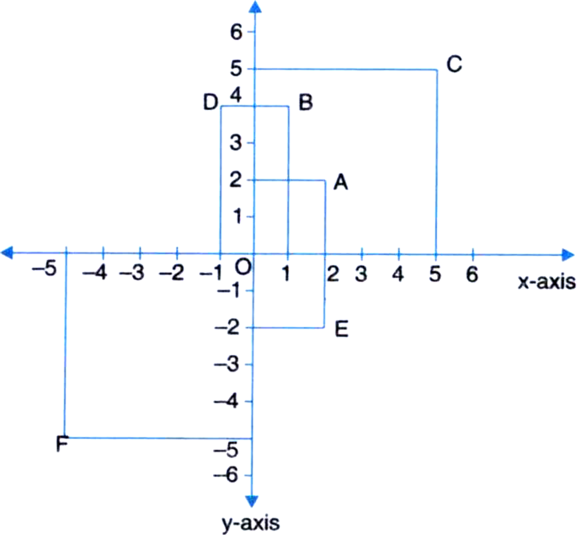
Solution not provided.
Ans.
![]()
In which quadrant or on which axis do each of the points (-2, 4), (3, -1),(-1, 0), (1, 2) and (-3, -5) lie ? Verify your answer by locating them on the Cartesian plane.
The point (-2, 4) lies in the II quadrant.
The point (3, -1) lies in the IV quadrant.
The point (-1, 0) lies on the negative x-axis.
The point (1, 2) lies in the I quadrant.
The point (-3, -5) lies in the III quadrant.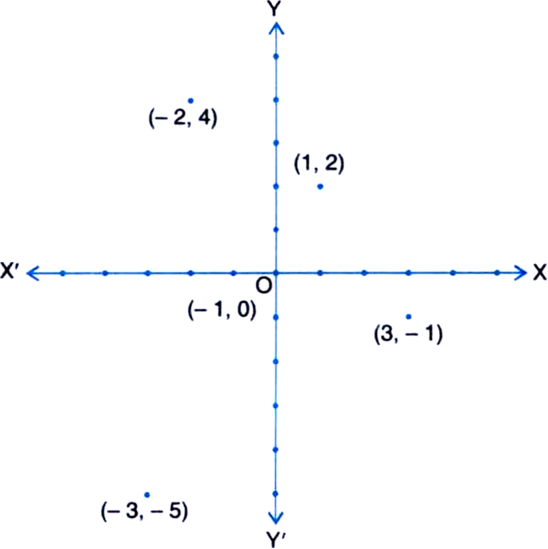
Name the quadrant in which the following points lie (-5, -4), (2, -4), (-7, 6) and (2, 3).
Plot the points A (3, 0), B (3, 3) and C (0, 3) in a Cartesian plane. Join OA, AB, BC and CO. Name the figure so formed and write its one property.
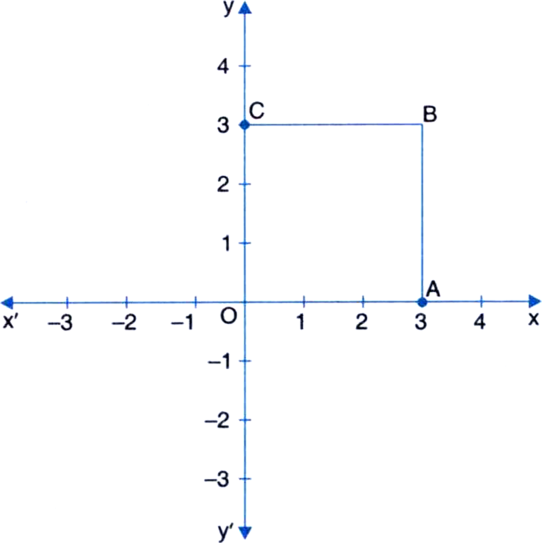
The figure formed is a square.
Its all the sides are of equal length.
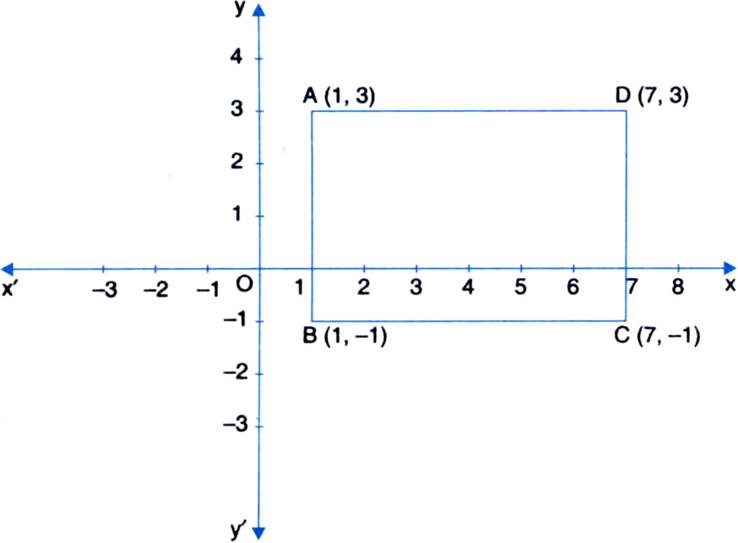
Plot the points A (1, 3), B (1, -1), C (7, -1) and D (7, 3) in Cartesian plane. Join them in order and name the figure so formed.
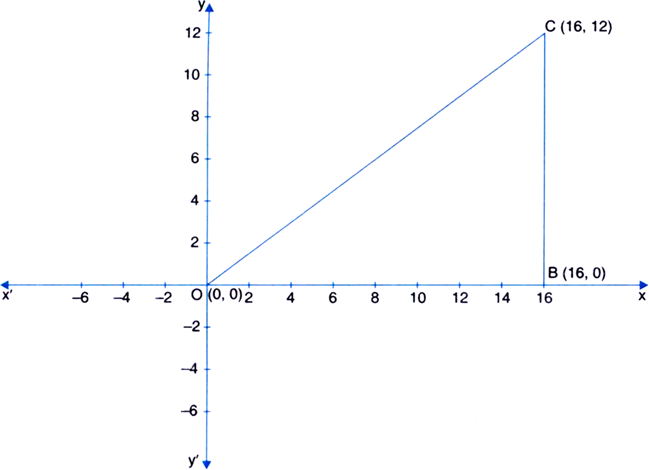
Plot the points O(0, 0), B( 16, 0), C( 16, 12) on the graph paper. Join O, B and C. Name the figure.
In figure, ABCD is a rectangle with length 6 cm and breadth 3 cm. O is the mid point of AB. Find the coordinates of A, B, C and D.
A → (-3, 0)
B → (3, 0)
C (3, 3)
D → (-3, 3)
Sponsor Area
Plot the points (2, 3), (-2, 3), (-2, -3) and (2, -3) on a graph sheet. Join these points. Name the figure obtained. Also, find the area of the figure so obtained.
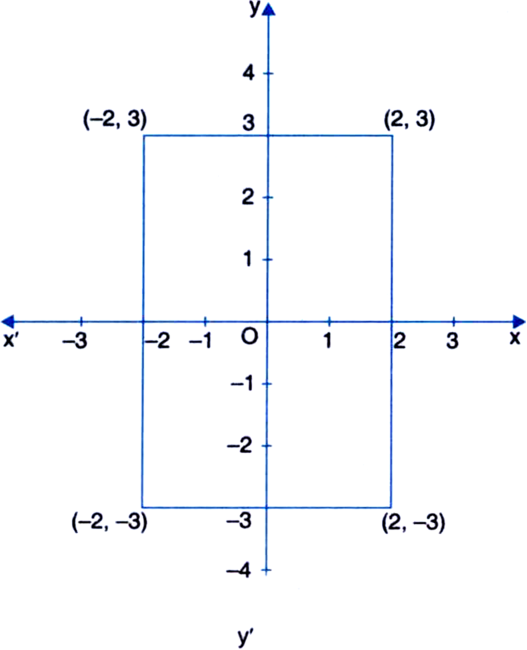
The figure obtained is a rectangle.
Area of the rectangle = 4 × 6 = 24 square units
Example 8. Mark the points (2, 2), (2, -2), (-2, -2) and (-2, 2) on a graph paper and join these points. Name the figure that you obtain. Also, find the area of the figure so obtained.
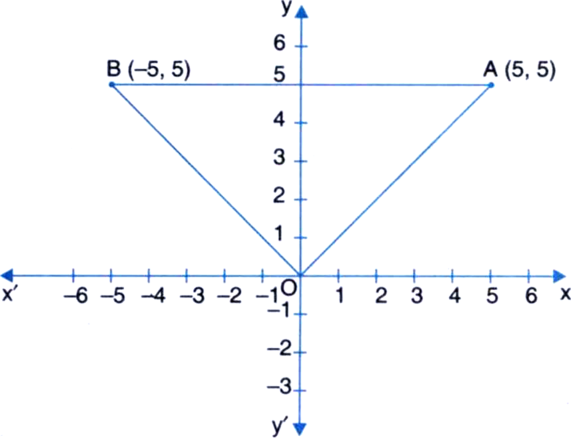
Plot the points A (5, 5) and B (-5, 5) in cartesian plane. Join AB, OA and OB. Name the figure obtained.
Which of the following points lie on x-axis? Which on y-axis?
A (0, 2), B (5, 6), C (-3, 0), D (0, -3), E (0, 4), F (6, 0), G (3, 0)
The points C, F and G lie on x-axis.
The points A, D and E lie on y-axis.
The following table gives the number of pairs of shoes and their corresponding price. Plot there as ordered pairs and join them. What type of graph do you get?

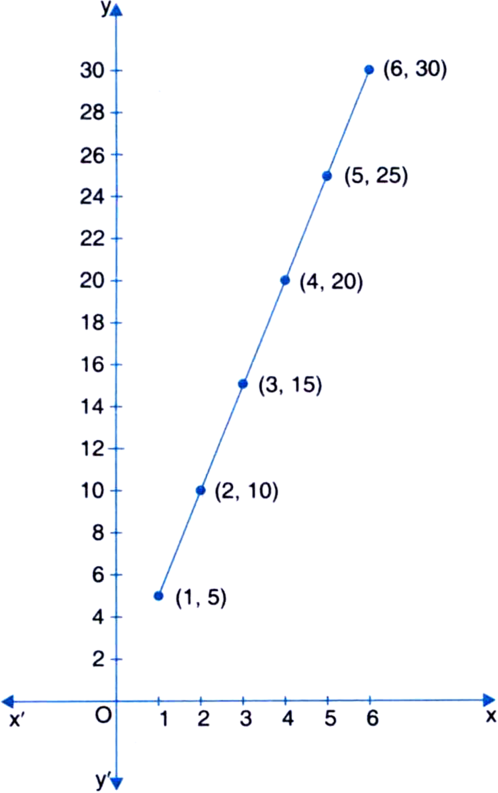
The graph we get is a straight line.
Plot the points A (4, 0) and B (0, 4). Join AB to the origin O. Find the area of
Solution not provided.
Ans. 32 square units.
The following table gives the number of pens and their corresponding costs. Plot these as ordered pairs and join them. What type of graph do you get?

Solution not provided.
Ans. Straight line
Plot the following points in the coordinate plane: P(3, 1); Q(8, 1); R(8, -3) and S(3, -3). What type of figure do you get by joining the points P, Q, R and S?
Solution not provided.
Ans. Rectangle
Plot the points A(2, 3), B(2, 1), C(0, 1) and D(0, 3). Join the points and identify the figure obtained. Find its area and perimeter.
Solution not provided.
Ans. Square; 4 Square units; 8 units
What are the co-ordinates of a point that is:
(i) the mirror image of point (0, 4) in x-axis
(ii) mirror image of point (-3, -5) in y-axis.
What are the co-ordinates of a point that is:
(i) the mirror image of point (0, 4) in x-axis
(ii) mirror image of point (-3, -5) in y-axis.
Solution not provided.
Ans. (i) (0, -4) (ii) (3, -5)
Sponsor Area
Where do the I and III quadrants meet?
-
in x-axis
-
in y-axis
-
at 0
-
do not intersect
C.
at 0Tips: -
The points (-5, 2) and (2, -5) lie in the:
-
Same quadrants
-
II and III quadrants respectively
-
II and IV quadrants respectively
-
IV and III quadrants respectively
D.
IV and III quadrants respectively
Abscissa of a point is positive in:
-
I and II quadrants
-
I and IV quadrants
-
I quadrant only
-
IV quadrant only
B.
I and IV quadrants
Which of the following is an example of a geometrical line?
-
Black Board
-
Sheet of paper
-
Meeting place of two walls
-
Tip of the sharp pencil
C.
Meeting place of two walls
Two planes intersect each other to form a:
-
plane
-
point
-
straight line
-
angle
C.
straight lineThe perpendicular distance of a point from the x-axis is 4 units and the perpendicular distance from the v-axis is 5 units. Write the coordinates of such a point if it lies in the
(a) I quadrant (b) II quadrant
(c) III quadrant (d) IV quadrant
Solution not provided.
Ans. (a) (5, 4) (b) (-5, 4) (c) (-5, -4) (d) (5, - 4)
Plot the points A(0, 3), B(5, 3), C(4, 0) and D(-1, 0) on the graph paper. Identify the figure ABCD and find whether the point (2, 2) lies in side the figure or not?
Solution not provided.
Ans. Parallelogram: yes
In which quadrant do the following points lie?
(a) (-6, 2) (b) (-5, -4)
(c)(3, -2) (d) (9, 6)
Solution not provided.
Ans. (a) II (b) III (c) IV (d) I
Find the co-ordinates of the vertices of a rectangle placed in III quadrant, in the Cartesian plane with length ‘p’ units on x-axis and breadth ‘q’ units on y-axis.
Solution not provided.
Ans. (0, 0), (-p, 0), (-p, -q), (0, -q)
Locate and write the co-ordinates of a point:
(a) above x-axis lying on y-axis at a distance of 5 units from origin
(b) below x-axis lying on y-axis at a distance of 3 units from origin.
(c) lying on x-axis to the right of origin at a distance of 5 units.
(d) lying on x-axis to the left of origin at a distance of 2 units.
Solution not provided.
Ans. (a) (0, 5) (b) (0, -3) (c) (5, 0) (d) (-2, 0)
If the co-ordinates of a point M are (2, 9) which can also be expressed as (1 + x, y2) and y > 0, then find in which quadrant do the following points lie:
P (y, x), Q (2, x), R (x2, y - 1), S (2x, - 3y)
Solution not provided.
Ans.
P → I
Q → I
R → I
S → IV
The area (∆OAB) = area (∆OPQ). Find the ordinate of point A.
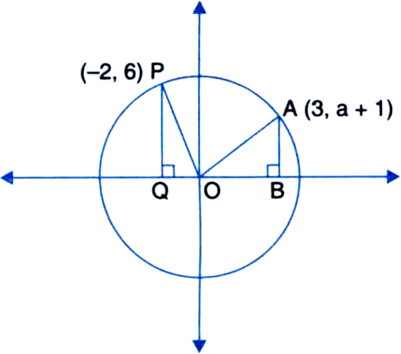
Solution not provided.
Ans. A → (3, 4)
Plot the following points, join them and identify the figure thus obtained:
P (-1, 0), Q (2, 0), R (2, 3) and S (-1, 5).
Solution not provided.
Ans. Trapezium
In which quadrant or on which axes the following points lie?
P (-2, 4), Q (3, -1), R (-1, 0) and S (0, -4).
Solution not provided.
Ans. (P) II (Q)IV (R) x-axis (S) y-axis
Points A (5, 3), B (-2, 3) and D (5, -4) are three vertices of a square ABCD. Plot these points on a graph paper and hence find the co-ordinates of vertex C.
Solution not provided.
Ans. C → (-2, -4)
Mock Test Series
Sponsor Area
Sponsor Area