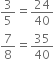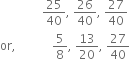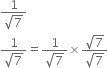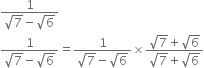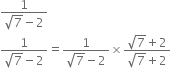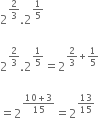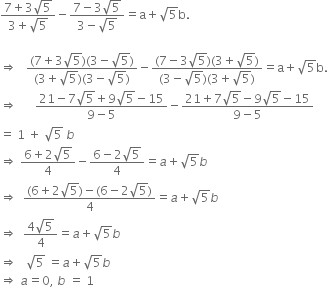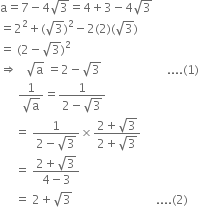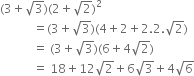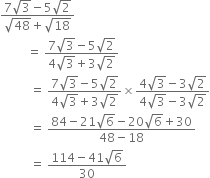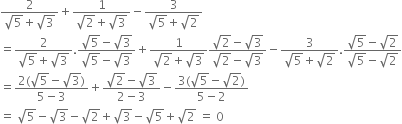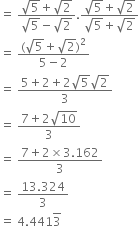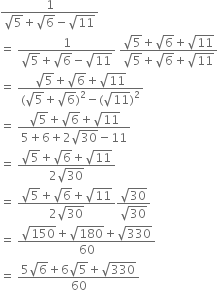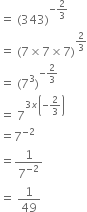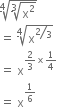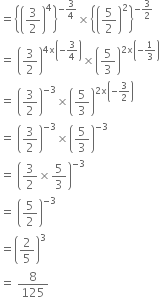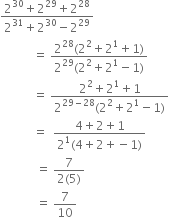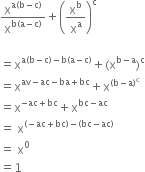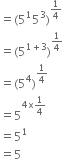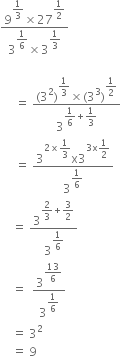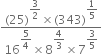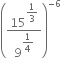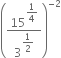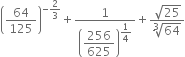Mathematics Chapter 2 Polynomials
Sponsor Area
NCERT Solution For Class 9 About 2.html
Is zero a rational number? Can you write it in the form  where p and q are integers and q ≠ 0?
where p and q are integers and q ≠ 0?
Note. Denominator q can also be taken as negative integer.
Find six rational numbers between 3 and 4.

Thus, six ratonal numbers between 3 and 4 are
Alter
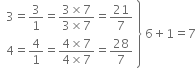
Thus, six rational numbers between 3 and 4 can be taken as
Note. This is known as the method of finding rational numbers in one step.
Find five rational numbers between 
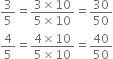
Therefore, five rational numbers between
State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
(i) True, since the collection of whole numbers contains all natural numbers.
(ii) False, for example, - 2 is an integer but not a whole number.
(iii) False, for example, ![]() is a rational number but not a whole number.
is a rational number but not a whole number.
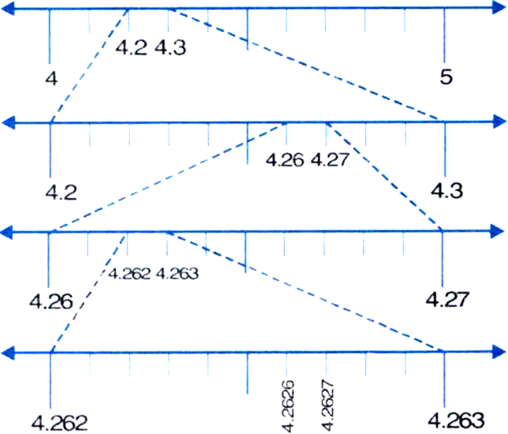
Find three rational numbers between 0 and 0.1. Also, find twenty rational numbers between 0 and 0.1.
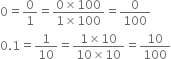
Thus, three rational numbers between 0 and 0.1 can be taken as
Again,
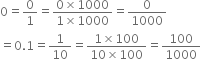
Thus, twenty rational numbers between 0 and 0.1 can be taken as

i.e., 0.001,0.002,0.003,0.004,0.005,0.006,0.007, 0.008,0.009,0.01,0.011,0.012,0.013,0.014,0.015, 0.016,0.017, 0.018, 0.019 and 0.02
Insert three rational numbers between ![]()

Thus, three rational numbers which can be inserted between
Are the following statements true or false? Give reasons for your answers.
(i) Every whole number is a natural number.
(ii) Every integer is a rational number.
(iii) Every rational number is an integer.
(i) False, because zero is a whole number but not a natural number.
(ii) True, because every integer m can be expressed in the form ![]() and so it is a rational number.
and so it is a rational number.
(iii) False, because ![]() is a rational number but not an integer.
is a rational number but not an integer.
State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form ![]() where m is a natural number.
where m is a natural number.
(iii) Every real number is an irrational number.
(i) True, since collection of real numbers is made up of rational and irrational numbers.
(ii) False, because no negative number can be the square root of any natural number.
(iii) False, for example, 2 is real but not irrational.
Sponsor Area
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Show how  can be represented on the number line.
can be represented on the number line.
Consider a unit square OABC and transfer it onto the number line making sure that the vertex O coincides with zero.
Then OB =
Construct BD of unit length perpendicular to OB.
Then OD =
Construct BD of unit length perpendicular to OB.
Then OE =
Construct BD of unit length perpendicular to OB.
Then OF =
Using a compass, with centre O and radius OF, draw an arc which intersects the number line in the point R. Then R corresponds to
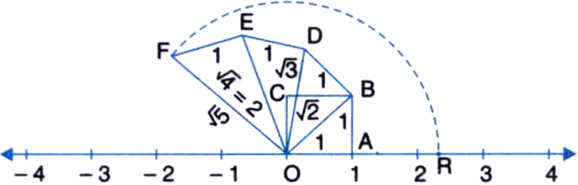
Representation of
Every point on the number line corresponds to a _____ number which may be either ___ or______
Real
,Rational Number
,Irrational Number
Write the following in decimal form and say what kind of decimal expansion each has:

Write the following in decimal form and say what kind of decimal expansion each has:
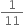

The decimal expansion is non-terminating repeating.
Write the following in decimal form and say what kind of decimal expansion each has:
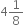

Write the following in decimal form and say what kind of decimal expansion each has:
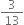

The decimal expansion is non-terminating repeating.
Write the following in decimal form and say what kind of decimal expansion each has:
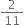
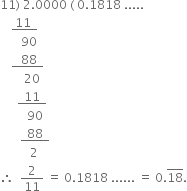
The decimal expansion is non-terminating repeating.
Write the following in decimal form and say what kind of decimal expansion each has:


The decimal expansion is terminating.
You know that 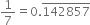 Can you predict what the decimal expansions of
Can you predict what the decimal expansions of
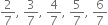 are, without actually doing the long division? If so, how?
are, without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of  carefully.]
carefully.]
Yes! We can predict the decimal expansions of ![]() without actually doing the long division as follows:
without actually doing the long division as follows:
![]()

To predict the decimal expansion of ![]() locate when the remainder becomes 2 and respective quotient (here it is 2). Then write the new quotient beginning from there using the repeating digits 1, 4, 2, 8, 5, 7.
locate when the remainder becomes 2 and respective quotient (here it is 2). Then write the new quotient beginning from there using the repeating digits 1, 4, 2, 8, 5, 7.![]()
Similarly,
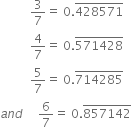
Express the following in the form  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.

Let ![]()
Multiplying both sides by 10 (since one digit is repeating), we get
10x = 6.666 .......![]() 10x = 6 + 0.6666 .....
10x = 6 + 0.6666 .....![]() 10x = 6 + x
10x = 6 + x![]() 10x - x = 6
10x - x = 6![]() 9x = 6
9x = 6![]()
![]()
![]()
![]()
Thus, ![]()
Here p = 2
q = 3 (![]() )
)
Express the following in the form 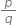 where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
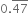
Let x = ![]() = 0.47777 ......
= 0.47777 ......
Multiplying both sides by 10 (since one digit is repeating), we get
10x = 4.7777 ......![]() 10x = 4.3 + 0.47777 .......
10x = 4.3 + 0.47777 .......![]() 10x = 4.3 + x
10x = 4.3 + x![]() 10x - x = 4.3
10x - x = 4.3![]() 9x = 4.3
9x = 4.3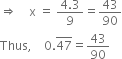
Here, p = 43
q = 90 (![]() )
)
Express the following in the form  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.

Let x = ![]()
Multiplying both sides by 1000 (since three digits are repeating), we get
1000x = 1.001001 .......![]() 1000x = 1 + 0.001001001 ........
1000x = 1 + 0.001001001 ........![]() 1000x = 1 + x
1000x = 1 + x![]() 1000x - x = 1
1000x - x = 1![]() 999x = 1
999x = 1![]()
![]()
Thus. ![]()
Here, p = 1
q = 999 ![]()
Express 0.99999...... in the form  Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Let x = 0.99999......
Multiplying both sides by 10 (since one digit is repeating), we get
10x = 9.9999 .........![]() 10x = 9 + 0.99999 ......
10x = 9 + 0.99999 ......![]() 10x = 9 + x
10x = 9 + x![]() 10x - x = 9
10x - x = 9![]() 9x = 9
9x = 9![]()
![]()
Thus, 0.99999 ....... = 1 = ![]()
Here, p = 1
q = 1
Since 0.99999......goes on for ever, so there is no gap between 1 and 0.99999......and hence they are equal.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 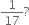 Perform the division to check your answer.
Perform the division to check your answer.
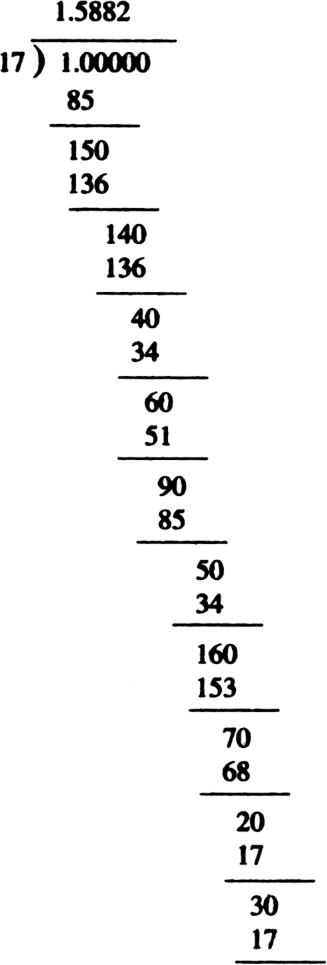
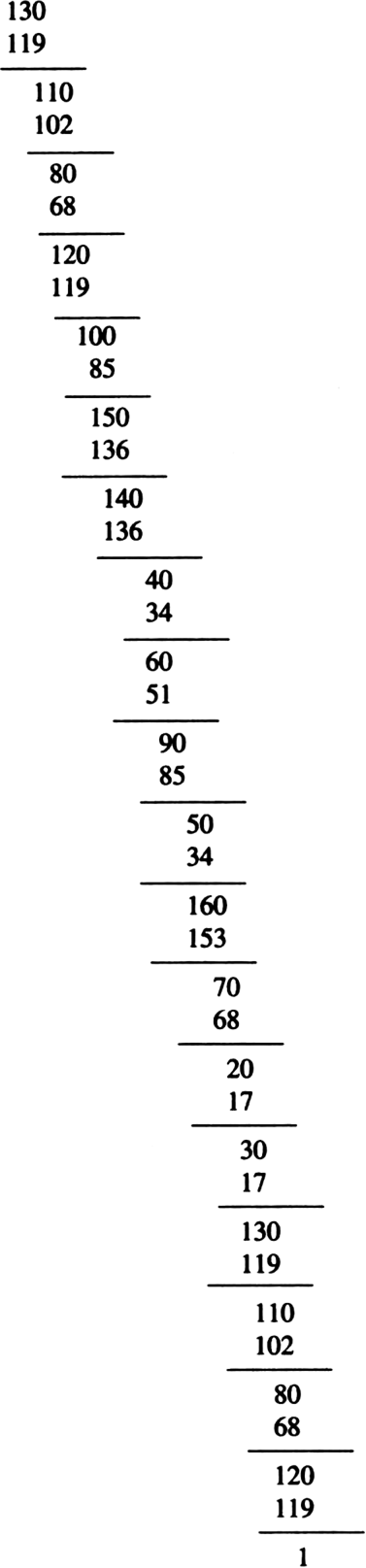
By Long Division, the number of digits in the repeating block of digits in the decimal
expansion of
∴ The answer is verified.
Sponsor Area
Look at several examples of rational numbers in the form 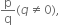 where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

The property that q must satisfy is that the prime factorisation of q must have only powers of 2 or powers of 5 or both.
Write three numbers whose decimal expansions are non-terminating non-recurring.
0.01001 0001 00001.......,
0.20 2002 20002 200002.......,
0.003000300003......,
Find three different irrational numbers between the rational numbers 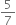 and
and

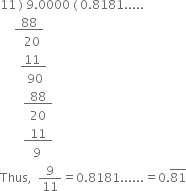
Three different irrational numbers between the rational numbers ![]() and
and ![]() can be taken as
can be taken as
0.75 075007500075000075......
0.7670767000767.......
0.808008000800008.......
Classify the following numbers as rational or irrational:


∵ The decimal expansion is non-terminating non-recurring.
Classify the following numbers as rational or irrational:

q = 1
Classify the following numbers as rational or irrational:
0.3796
0.3796
∵ The decimal expansion is terminating.
∴ 0.3796 is a rational number.
Classify the following numbers as rational or irrational:
7.478478......
∵ The decimal expansion is non-terminating recurring.
∴ 7.478478......is a rational number.
Classify the following numbers as rational or irrational:
1.101001000100001......
1.101001000100001......
∵ The decimal expansion is non-terminating non-recurring.
∴ 1.101001000100001...... is an irrational number.
Find two irrational numbers between 0.1 and 0.12.
The two irrational numbers between 0.1 and 0.12 can be taken as
0.1010010001......
and 0.11010010001.....
Find two irrational numbers between 2 and 2.5.
First Method
The two irrational numbers between 2 and 2.5 can be taken as
2.101001000100001......
and 2.201001000100001.......
Second Method
Note: If a and b are two distinct positive rational numbers such that ab is not a perfect square of a rational number, then ![]() is an irrational number lying between a and b.
is an irrational number lying between a and b.
∴ An irrational number between 2 and 2.5![]()
Similarly, an irrational number between 2 and ![]()
![]()
∴ Two irrational numbers between 2 and 2.5 are ![]() and
and ![]()
Give two rational numbers lying between
0.232 332 333 2 3333 2...... and 0.212 112 111 2 1111......
Two rational numbers lying between
0.232 332 333 2 3333 2......
and 0.212 112 111 2 1111......
can be taken as 2.221 and 2.222.
Find one irrational number between the numbers a and b given below:
a = 0.1111 ........ = 
b = 0.1101.
Find two rational numbers in the form  between 0.34 344 3444 34444 3 ...... and 0.36 366 3666 36666 3......
between 0.34 344 3444 34444 3 ...... and 0.36 366 3666 36666 3......
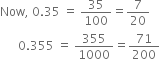
Express  in the form
in the form  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
![]()
⇒ x = 5.3474747......
⇒ 10x = 53.474747...... ...(1)
⇒ 1000x = 5347.474747...... ...(2)
Subtracting (1) from (2), we get
990x = 5294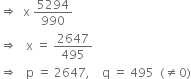
Express ![]() in the form of
in the form of ![]() where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
Let ![]()
Then, x = 0.001 001 001 001...... ...(1)
⇒ 1000x = 1.001 001 001 001...... ...(2)
Subtracting (1) from (2), we get
99x = 1![]()
![]()
Express  in the form of
in the form of  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
⇒ x = 5.2222...... ...(1)
⇒ 10x = 52.2222...... ...(2)
Subtracting (1) from (2), we get
9x = 47
How many irrational numbers lie between  and
and  Find any three irrational numbers lying between
Find any three irrational numbers lying between  and
and 
Infinitely many irrational numbers lie between ![]() and
and ![]()
One irrational number between ![]() and
and ![]() is
is![]()
Another irrational number between ![]() and
and ![]() is
is ![]()

Third irrational number between ![]() and
and ![]() is
is ![]()
Find two irrational numbers between  and
and 
One irrational number is ![]()
Another irrational number is ![]()
Find the decimal expansions of 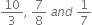 and
and
Solution not provided.
Ans. 3.3333...... = ![]() 0.875; 0.142857 142857 .......
0.875; 0.142857 142857 .......
Show that 3.142678 is a rational number. In other words, express 3.142678 in the form  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
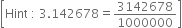
Solution not provided.![]()
Show that 0.3333..... =  can be expressed in the form
can be expressed in the form  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
Solution not provided.
Ans. ![]()
Show that  can be expressed in the form
can be expressed in the form  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
Solution not provided.
Ans. ![]()
Show that 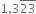 can be expressed in the form
can be expressed in the form  where p and q are integers and q ≠ 0.
where p and q are integers and q ≠ 0.
Solution not provided.
Ans. ![]()
Express  as a rational number in the form where p and q are integers and q ≠ 0.
as a rational number in the form where p and q are integers and q ≠ 0.
Solution not provided.
Ans. ![]()
Classify the following numbers as rational or irrational:

Classify the following numbers as rational or irrational:
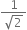
Classify the following numbers as rational or irrational:
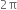
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is,  This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
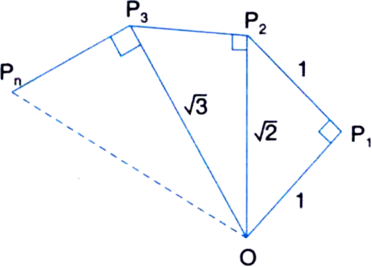
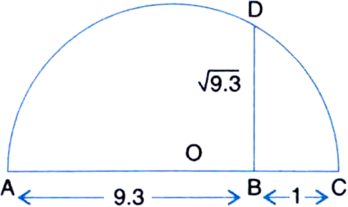
Represent  on the number line.
on the number line.

Mark the distance 9.3 from a fixed point A on a given line to obtain a point B such that AB = 9.3 units. From B mark a distance of 1 unit and mark the new point as C. Find the mid-point of AC and mark that point as O. Draw a semi-circle with centre O and radius OC. Draw a line perpendicular to AC passing through B and intersecting the semi-circle at D. Then
Sponsor Area
Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers.
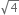
Its decimal represenation is 2.0
Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers.

Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers.

q = 5
Its decimal representation is 1.2
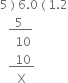
Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers.
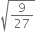
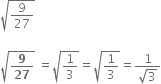
Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers.

which is a rational number
q = 5
Its decimal representation is - 0.8
Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers.

which is a rational number.
Its decimal representation is 10.0.
In the following equations, find which variables x, y, z etc., represent rational numbers and which represent irrational numbers:
x2 = 5
x2 = 5
x2 = 5 ![]()
In the following equations, find which variables x, y, z etc., represent rational numbers and which represent irrational numbers:
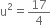
In the following equations, find which variables x, y, z etc., represent rational numbers and which represent irrational numbers:

which is a rational number.
In the following equations, find which variables x, y, z etc., represent rational numbers and which represent irrational numbers:

which is an irrational number since the decimal expansion is non-terminating non-recurring.


Rationalise the denominators of the following:
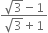
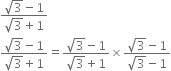
Multiplying the numerator and denominator by
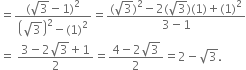
Rationalise the denominators of the following:
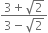
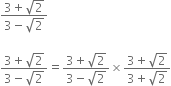
Mul;tiplying the numerator and denominator by
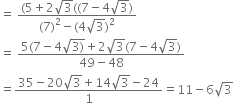
Rationalise the denominators of the following:
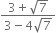
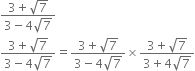
Multliplying the numerator and denominator by
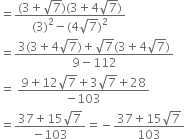
Represent  on the number line.
on the number line.
Then, ![]()
Now, let us treat the line BC as the number line, with B as zero, C as 1, and so on. Draw an arc with centre B and radius BD, which intersects the number line in E.
Then, E represents ![]()
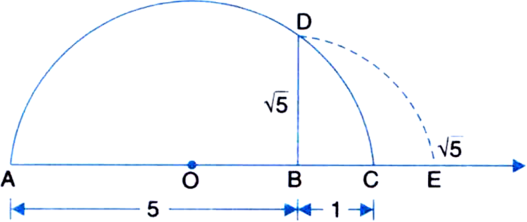
Represent 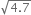 on the number line.
on the number line.

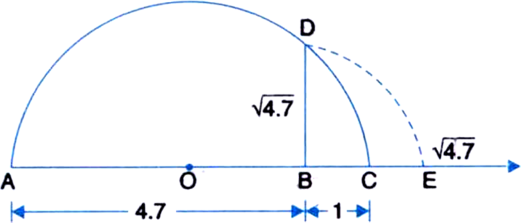
Now, let us treat the line BC as the number line, with B as zero, C as 1, and so on. Draw an arc with centre B and radius BD, which intersects the number line in E.
Then, E represents ![]()
Check whether 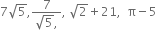 are irrational numbers or not.
are irrational numbers or not.
Sollution not provided.
All are irrational numbers.
Sponsor Area
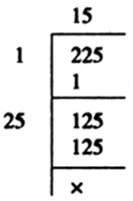
Find the value of ‘p’ if 5p-3 × 32p - 8 = 225.
5p - 3 × 32p - 8 = 225
⇒ 5p - 3 × 32p - 8 = 52 × 32
⇒ p – 3 = 2
2p - 8 = 2
⇒ p = 5
Find a point corresponding to 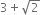 on the number line.
on the number line.
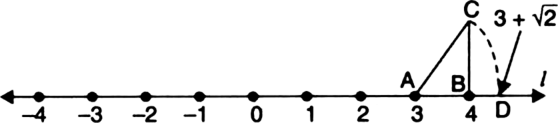
the number line at the point D. Then, point D represents
Prove that  is an irrational number.
is an irrational number.
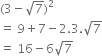
Again, 16 is a rational number and
Write three numbers whose decimal expansions are non-terminating non-recurring.
0.01001 0001 00001.......,
0.20 2002 20002 200002.......,
0.003000300003......,
Let ‘a’ he a rational number and ‘b’ be an irrational number. Is ‘ab’ necessarily an irrational? Justify your answer with an example.
a = 0 and b = ![]()
Then, ab = 0 x ![]() which is rational.
which is rational.
Hence, 'ab' is not necessarily an irrational.
Prove that  is an irrational number.
is an irrational number.
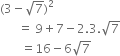
Again, 16 is a rational number and
Find the value of ‘p’ if 5p-3 × 32p - 8 = 225.
5p - 3 × 32p - 8 = 225
⇒ 5p - 3 × 32p - 8 = 52 × 32
⇒ p – 3 = 2
2p - 8 = 2
⇒ p = 5
If a = 2, b = 3, then find the values of the following:
(i) (ab + ba)-1 (ii) (aa + bb)-1
(i) (ab+ba)-1
= (23 + 32)-1
= (8 + 9)-1
= (17)-1
= ![]()
(ii) (aa + bb)
= (22 + 33)-1
= (4 + 27)-1
= (31)-1
![]()
Show that
(xa - b)a + b. (xb - c)b + c. (xc - a)c + a = 1
(xa - b)a + b. (xb - c)b + c. (xc - a)c + a
= x(a - b) (a + b). x(b - c) (b + c). x(c - a) (c + a)
= xa2 - b2. xb2 - c2. xc2 - a2
= xa2 - b2 b2 + b2 - c2 + c2 - a2
= X0
= 1
Write the following in the ascend ing order of their magnitude 
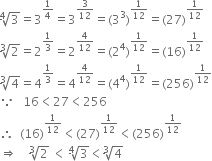
Hence, the ascending order is
If ‘x’ is a positive real number and exponents are rational numbers, simplify:
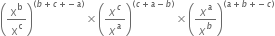
Solution not provided.
Ans. 1
Which of the following is a rational number?
-

-

-
0.101 001 0001 00001......
-
0.85 385 3853 ......
D.
0.85 385 3853 ......
2. π is:
-
a rational number
-
an integer
-
an irrational number
-
a whole number
a whole number
C.
an irrational number
A number is an irrational if and only if its decimal representation is:
-
non-terminating
-
non-terminating and repeating
-
non-terminating and non-repeating
-
terminating
C.
non-terminating and non-repeating
Which one of the following is an irrational number?
-
0.14
-
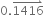
-

-
0.401 4001 4 00014......
0.14
0.401 4001 4 00014......
D.
0.401 4001 4 00014......
Which of the following is irrational number?
-
0.15
-

-

-
0.501 5001 50001 ......
0.15
0.501 5001 50001 ......
D.
0.501 5001 50001 ......
The decimal expansion of  is:
is:
-
finite decimal
-
1.4121
-
non-terminating recurring
-
non-terminating non-recurring
D.
non-terminating non-recurring
 when simplified is:
when simplified is:
-
positive and irrational
-
positive and rational
-
negative and irrational
-
negative and rational
B.
positive and rational
 when simpli fied is:
when simpli fied is:
-
positive and irrational
-
negative and irrational
-
positive and rational
-
negative and rational
C.
positive and rational
An irrational number between  is:
is:
-
0.75
-

-
0.750 7500 75000 .......
-
0.7512
0.75
0.750 7500 75000 .......
0.7512
C.
0.750 7500 75000 .......
Every rational number is:
-
a natural number
-
an integer
-
a real number
-
a whole number
C.
a real number
A terminating decimal is:
-
natural number
-
a whole number
-
a rational number
-
an integer
C.
a rational number
Which of the following is an irrational number?
-

-
3.763
-

-
3.1011 0011 0001 .......
3.763
3.1011 0011 0001 .......
D.
3.1011 0011 0001 .......
Mock Test Series
Sponsor Area
Sponsor Area






![<pre>uncaught exception: <b>file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/3c/da/d4a3938b4d71e2799d196755596e.ini): failed to open stream: Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php at line #12file_put_contents(/home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/web/../../../../../../formulas/3c/da/d4a3938b4d71e2799d196755596e.ini): failed to open stream: Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php line 12<br />#0 [internal function]: _hx_error_handler(2, 'file_put_conten...', '/home/config_ad...', 12, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/sys/io/File.class.php(12): file_put_contents('/home/config_ad...', 'mml=<math xmlns...')
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(48): sys_io_File::saveContent('/home/config_ad...', 'mml=<math xmlns...')
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(112): com_wiris_util_sys_Store->write('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#6 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#7 {main}</pre>](/application/zrc/images/qvar/MAEN9054119-1.png)