Physics Part Ii Chapter 9 Ray Optics And Optical Instruments

a) When an unpolarized light falls on a polaroid, only those electric vectors that are oscillating along a direction perpendicular to the aligned molecules will pass through. Thus, incident light gets linearly polarized.

Electric vectors which are along the direction of the aligned molecules gets absorbed.

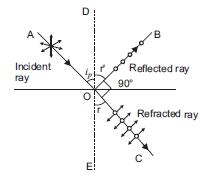
Whenever unpolarized light is incident on the boundary between two transparent media, the reflected light gets partially or completely polarized. When reflected light is perpendicular to the refracted light, the reflected light is a completely polarized light.

No, it will not suffer total internal reflection

$$\begin{gathered} {\mathrm{a}}_{\mathrm{\mu w}} = \frac{{\mathrm{\mu }}_{\mathrm{w}}}{{\mathrm{\mu }}_{\mathrm{s}}} = \frac{{\displaystyle \raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}} = \frac{8}{9} \\ \mathrm{i} = {\sin }^{-1} \left(\mathrm{\mu }\right) = {\sin }^{-1}\left(\frac{8}{9}\right) = 62.{73}^0 \end{gathered}$$

so if i is less than 60^o then TIR will not happen

Let,

f = focal length liquid +lens

f₁ = focal length of lens

f₂ = focal length of liquid mirror

$$\begin{gathered} \frac{1}{\mathrm{f}} =\frac{1}{{\mathrm{f}}_1} + \frac{1}{{\mathrm{f}}_2} \\ \frac{1}{{\mathrm{f}}_2} = \frac{1}{\mathrm{f}}-\frac{1}{{\mathrm{f}}_1} \\ \frac{1}{{\mathrm{f}}_2} = \frac{1}{\mathrm{x}} -\frac{1}{\mathrm{y}} \\ {\mathrm{f}}_2 = \frac{\mathrm{xy}}{\mathrm{y} - \mathrm{x}} \\ \mathrm{Now}, \\ \frac{1}{{\mathrm{f}}_1} = (\mathrm{\mu } -1)\left(\frac{2}{\mathrm{R}}\right) (\mathrm{convex} \mathrm{lens}) \\ \frac{1}{\mathrm{y}} = (1.5 - 1)\frac{2}{\mathrm{R}} \\ \frac{1}{\mathrm{y}} = \frac{0.5 \mathrm{x} 2}{\mathrm{R}} \\ \mathrm{R} = \mathrm{y} \\ \mathrm{Now} \mathrm{for} \mathrm{liquid} \\ \frac{1}{{\mathrm{f}}_2} = (\mathrm{\mu }\text{'}-1)\left(\frac{1}{\mathrm{R}}\right) \\ -\frac{(\mathrm{y}- \mathrm{x})}{\mathrm{xy}} = \left(\mathrm{\mu }\text{'} - 1\right)\left(\frac{1}{\mathrm{R}} -\frac{1}{\infty }\right) \\ - \frac{(\mathrm{y} -\mathrm{x})}{\mathrm{xy}} = \frac{{\displaystyle \left(\mathrm{\mu }\text{'} - 1\right)}}{\mathrm{y}} \\ \therefore \frac{\mathrm{x}-\mathrm{y}}{\mathrm{x}} = \mathrm{\mu }\text{'} - 1 \\ 1 + 1 - \frac{\mathrm{y}}{\mathrm{x}} =\mathrm{\mu }\text{'} \\ 2 - \frac{\mathrm{y}}{\mathrm{x}} = \mathrm{\mu }\text{'} \end{gathered}$$

Ray Diagram:

1. Spherical and chromatic abbreviation eliminated.
2. Objective lenses are large and expensive in refracting telescope, where as reflecting telescope is economical.

A relationship among the object distance (u), the image distance (v) and the focal length (f) of a mirror are called the mirror formula.

The formula is given by $\frac{1}{\mathrm{f}} = \frac{1}{\mathrm{u}} +\frac{1}{\mathrm{v}}$

Take an object AB beyond C of a concave mirror MM'. A ray AD parallel to principal axis passes through focus after reflection.

Another ray AE which is passing through C comes back along the same path after reflection. 

These two reflected rays intersect at A'. A' draw perpendicular A'B' on the principal axis. So A'B' is a real and inverted image which is formed between C and F which is smaller than the object in size.

Draw DG perpendicular to the principal axis. So, applying sign convention, we get

PB = - u,

PB' = -v

PF = -f

PC = -2f

Now, In △ABC and △A'B'C, ∠ABC =∠A'B'C = 90°

∠ACB = ∠A'CB' (Vertically Opposite angles)
∴ △ABC ~△A'B'C (AA similarity)

$\frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}} = \frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}\text{'}}$ (the corresponding side of similar triangles are in proportion)..... (1)

In △DGF and △A'B'F, ∠DGF = ∠A'B'F = 90°

∠DGF= ∠A'FB' (vertically opposite angles)

△DGF ~△A'B'F (AA similarity)

$\frac{\mathrm{DG}}{\mathrm{A}\text{'}\mathrm{B}\text{'}} = \frac{\mathrm{GF}}{\mathrm{B}\text{'}\mathrm{F}\text{'}}$(corresponding sides of similar triangles are in proportion)

But AB = DG (the perpendicular distance between two parallel lines are equal)

$$\begin{gathered} \therefore \frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}} = \frac{\mathrm{GF}}{\mathrm{B}\text{'}\mathrm{F}\text{'}}.... \left(2\right) \\ \mathrm{From} \mathrm{eq} \left(1\right) \mathrm{and} \left(2\right), \mathrm{we} \mathrm{get}, \\ \frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}} = \frac{\mathrm{GF}}{\mathrm{B}\text{'}\mathrm{F}} ... \left(3\right) \end{gathered}$$

Let us assume the mirror is very small,

∴ G and P are very close to each other so that GF = PF.

From equation (3),

$$\begin{gathered} \frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}} = \frac{\mathrm{PF}}{\mathrm{B}\text{'}\mathrm{F}} \\ \Rightarrow \frac{\mathrm{PB} - \mathrm{PC}}{\mathrm{PC} - \mathrm{PB}\text{'}} \\ = \frac{\mathrm{PF}}{\mathrm{PB}\text{'} - \mathrm{PF}} \\ \Rightarrow \frac{-\mathrm{u} -(-2\mathrm{f})}{-2\mathrm{f}- (-\mathrm{v})} = \frac{{\displaystyle -\mathrm{f}}}{-\mathrm{v}-(-\mathrm{f})} \\ \Rightarrow \frac{-\mathrm{u} + 2\mathrm{f}}{-2\mathrm{f} + \mathrm{v}} = \frac{-\mathrm{f}}{-\mathrm{v} +\mathrm{f}} \\ \Rightarrow (-\mathrm{v} +\mathrm{f})(-\mathrm{u} +2\mathrm{f}) \\ =-\mathrm{f}(-2\mathrm{f} +\mathrm{v}) \\ \Rightarrow \mathrm{vu} -2\mathrm{fv}-\mathrm{fu} + 2{\mathrm{f}}^2 \\ = 2{\mathrm{f}}^2 - \mathrm{fv} \\ \Rightarrow \mathrm{uv} = - \mathrm{fv} + 2\mathrm{f} \\ \mathrm{v} +\mathrm{fu} \\ \therefore \mathrm{uv} = \mathrm{vf} + \mathrm{uf} \\ \mathrm{Dividing} \mathrm{both} \mathrm{sides} \mathrm{by} \mathrm{uvf} \\ \frac{\mathrm{uv}}{\mathrm{uvf}} = \frac{\mathrm{vf}}{\mathrm{uvf}} + \frac{\mathrm{uf}}{\mathrm{uvf}} \\ \Rightarrow \frac{1}{\mathrm{f}} = \frac{1}{\mathrm{u}} + \frac{1}{\mathrm{v}} \end{gathered}$$

If the mirror is plane, the size of the image is always equal to the size of the object i.e., magnification is unity. But the case is different for a curved mirror. The size of the image is different from the size of the object in such a 'mirror'. The image may be greater or smaller in size than the object depending upon the nature of the mirror or the location of the object.

Let I and O be the size of the image and the object respectively. The ratio I/O is called magnification, and it is denoted by m.

Magnification, m = I/O = -v/u

This is called linear magnification.

A.

(2f, 2f)

It is possible when object kept at centre of curvature.
u = v
u = 2f,
v = 2f.

C.

A.

a vernier scale provided on the microscope

B.

-10 cm

P = P₁ + P₂ = −10
f= 1/P
 = 0.1 m 
 = -10 cm

A.

20 cm

D.

tan⁻¹ (n)

Brewster’s law: According to this law the ordinary light is completely polarised in the plane of incidence when it gets reflected from transparent medium at a particular angle known as the angle of polarisation. n = tan ip.

A.

cot²θ = cot²θ₁+ cot²θ₂

C.

3:2

A.

y/2x

When the mirror is rotated by θ angle reflected ray will be rotated by 2θ.

y/x = 2θ

θ = y/2x

B.

6°

(μ -1)A + (μ'-1)A = 0
(μ-1)A |(μ'-1)A'|
(1.42 -1)x10° = (1.7 -1)A'
4.2 = 0.7A'
A' = 6°

D.

Large focal length and large diameter

For a telescope, angular magnification =$\frac{f_0}{f_E}$ so, focal length of objective lens should be large, Angular resolution = $= \frac{D}{1.22\lambda }$so, D should be large. So, objective lens of refracting telescope should have large focal length (f₀) and large diameter D for larger angular magnification.

B.

45°

For retracing the path, light ray should be normally incident on silvered face.

$$\begin{gathered} A = r + O \\ \Rightarrow r = {30}^o \end{gathered}$$

Applying Snell's law at point M,
$$\begin{gathered} \frac{Sin i}{Sin {30}^o} = \frac{\sqrt{2}}{1} \\ \Rightarrow \sin i = \sqrt{2} x \frac{1}{2} \\ \Rightarrow \sin i = \sqrt{2 } x \frac{1}{2} \\ Or \sin i = \frac{1}{\sqrt{2}} i.e., i = {45}^o \end{gathered}$$

B.

36 cm away from the mirror

Using mirror formula,

 $$\begin{gathered} \frac{1}{f} = \frac{1}{v_1} +\frac{1}{u} \\ -\frac{1}{15} = \frac{1}{v_1} +\frac{1}{u} \\ \Rightarrow \frac{1}{v_1} = \frac{1}{-15} + \frac{1}{40} \\ \therefore = - 24 cm \end{gathered}$$

When object is displaced by 20 cm towards mirror Now, 

u₂ = -20

So, 

$$\begin{gathered} \frac{1}{f} = \frac{1}{v_2 } + \frac{1}{u_2} \\ \frac{1}{-15} = \frac{1}{v_2} - \frac{1}{20} \\ \Rightarrow \frac{1}{v_2} = \frac{1}{20}-\frac{1}{15} \end{gathered}$$

Therefore, image shifts away from mirror by  = 60-24 = 36 cm

C.

R/(μ -1)

When an object is placed in front of such a lens, the rays first of all refracted from the convex surface, then refract from the polished plane surface and again refracts from convex surface. If f_l and f_m be the focal lengths of lens (convex surface) and mirror (plane polished surface) respectively, then effective focal length F is given by

$$\begin{gathered} \frac{1}{\mathrm{F}} = \frac{1}{{\mathrm{f}}_{\mathrm{l}}} + \frac{1}{{\mathrm{f}}_{\mathrm{m}}} + \frac{1}{{\mathrm{f}}_{\mathrm{l}}} \\ = \frac{2}{{\mathrm{f}}_{\mathrm{l}}} + \frac{1}{{\mathrm{f}}_{\mathrm{m}}} = \frac{2}{{\mathrm{f}}_{\mathrm{l}}} \left(\because {\mathrm{f}}_{\mathrm{m}} = \frac{\mathrm{R}}{2} = \infty \right) \\ \frac{1}{{\mathrm{f}}_{\mathrm{l}}} = (\mathrm{\mu } - 1)\frac{1}{\mathrm{R}} \\ \therefore \frac{1}{\mathrm{F}} = \frac{2(\mathrm{\mu } -1)}{\mathrm{R}} \\ \mathrm{or} \mathrm{F} = \frac{\mathrm{R}}{2(\mathrm{\mu } -1)} \\ \mathrm{Or} \\ \mathrm{R} = 2\mathrm{F} = \frac{\mathrm{R}}{(\mathrm{\mu } - 1)} \end{gathered}$$

A.

45⁰

The ratio of the velocity of light in a vacuum to its velocity in a specified medium.

The relation for refractive index of prism is

$$\begin{gathered} \mathrm{\mu } =\frac{\sin \mathrm{i}}{\sin \mathrm{r}} \left(1\right) \\ \mathrm{The} \mathrm{condition} \mathrm{for} \mathrm{minimum} \mathrm{deviation} \mathrm{is} \\ \mathrm{r} = \frac{\mathrm{A}}{2} = \frac{{60}^0}{2}={30}^0 \\ \mathrm{Putting} \mathrm{the} \mathrm{value} \mathrm{of} \mathrm{\mu } =\sqrt{2} \& \mathrm{r} ={30}^0 \mathrm{in} \mathrm{equation} \left(1\right) \mathrm{we} \mathrm{get} \\ \sqrt{2} = \frac{\sin \mathrm{i}}{\sin {30}^0} \\ \sin \mathrm{i} =\sqrt{2} \times \frac{1 }{2} =\frac{1}{\sqrt{2}} \\ \sin \mathrm{i} = {45}^0 \because \sin {45}^{0 }=\frac{1}{\sqrt{2}} \end{gathered}$$

D.

40 cm

For refraction through a spherical interface (from medium 1 to 2 of refractive index n₁ and n₂ respectively)

$$\begin{gathered} \frac{{\mathrm{n}}_2}{\mathrm{\nu }} - \frac{{\mathrm{n}}_1}{\mathrm{\mu }}= \frac{{\mathrm{n}}_2-{\mathrm{n}}_1}{\mathrm{R}} \\ \mathrm{Thin} \mathrm{lens} \mathrm{formula} \\ \frac{1}{\mathrm{\mu }} - \frac{1}{\mathrm{\nu }} = \frac{1}{\mathrm{f}} \end{gathered}$$

Lens maker formula

$\frac{1}{\mathrm{f}} = \frac{\left({\mathrm{n}}_2-{\mathrm{n}}_1\right)}{{\mathrm{n}}_1} \left(\frac{1}{{\mathrm{R}}_1}-\frac{1}{{\mathrm{R}}_2}\right)$

Using the relation for focal length of planoconvex lens

$$\begin{gathered} =\frac{1}{\mathrm{f}}=\left( \mathrm{\mu } - 1\right) \left(\frac{1}{{\mathrm{R}}_1} - \frac{1}{{\mathrm{R}}_2}\right) \\ \mathrm{Refractive} \mathrm{index} \mathrm{of} \mathrm{material} \mathrm{of} \mathrm{lens} \mathrm{\mu }=1.5 \mathrm{cm}, {\mathrm{R}}_1=20 \mathrm{cm} \mathrm{and} {\mathrm{R}}_2=\infty \\ \frac{1}{\mathrm{f}} = \left(1.5 - 1\right) \left(\frac{1}{20} - \frac{1}{\infty }\right) \\ \Rightarrow \frac{1}{\mathrm{f}} = \frac{1}{40} \\ \mathrm{or} \mathrm{f} = 40 \mathrm{cm} \end{gathered}$$

B.

${\left(\frac{\mathrm{f}}{\mathrm{u}-\mathrm{f}}\right)}^2 \mathrm{b}$

Using the relation for the focal length of concave mirror

$$\begin{gathered} \frac{1}{\mathrm{f}} = \frac{1}{\mathrm{u}}+\frac{1}{\mathrm{\nu }} ...1 \\ \mathrm{Differentiating} \mathrm{equation} \left(1\right) \mathrm{we} \mathrm{get} \\ 0 = -\frac{1}{{\mathrm{\nu }}^2}\mathrm{dv} -\frac{1}{{\displaystyle {\mathrm{u}}^2}}\mathrm{du} \\ \Rightarrow \mathrm{d\nu } =-\frac{{\mathrm{\nu }}^2}{{\mathrm{u}}^2}\times \mathrm{b} (\mathrm{here} :- \mathrm{du} =\mathrm{b}) \\ \mathrm{From} \mathrm{equation} \left(1\right) \\ \frac{1}{\mathrm{\nu }}=\frac{1}{\mathrm{f}}-\frac{1}{\mathrm{u}} =\frac{\mathrm{u}-\mathrm{f}}{\mathrm{f} \mathrm{u}} \\ \mathrm{or} \frac{\mathrm{u}}{\mathrm{v}} =\frac{\mathrm{u}-\mathrm{f}}{\mathrm{f}} \\ \frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{f}}{\mathrm{u}-\mathrm{f}} \\ \mathrm{Now} \mathrm{from} \mathrm{equations} \left(2\right) \mathrm{and} \left(3\right) \mathrm{we} \mathrm{get} \\ \mathrm{dv} =-{\left(\frac{\mathrm{f}}{\mathrm{u}-\mathrm{f}} \right)}^2 \mathrm{b} \end{gathered}$$

∴$\mathrm{size} \mathrm{or} \mathrm{image} \mathrm{is}={\left(\frac{\mathrm{f}}{\mathrm{u}-\mathrm{b}}\right)}^2\mathrm{b}$

B.

$\sin \mathrm{\theta } \ge \frac{11}{13}$

Using the formula

$$\begin{gathered} {\mathrm{\mu }}_{\mathrm{prism} }=\frac{{\mathrm{\mu }}_{\mathrm{liquid}}}{{\mathrm{\mu }}_{\mathrm{prism}}} =\frac{1.32}{1.56} \\ =\frac{11}{13} \\ \mathrm{Now} \mathrm{the} \mathrm{condition} \mathrm{for} \mathrm{total} \mathrm{internal} \mathrm{reflection}, \mathrm{occur} \mathrm{when} \sin \mathrm{\theta } \ge \mathrm{\mu } \\ \mathrm{so} \sin \mathrm{\theta } \ge \frac{11}{13} \end{gathered}$$

B.

1.4

The ratio of the sine of the angle of incidence to the sine of angle of refraction is constant. The angles of incidence (i ) and refraction (r ) are the angles that the incident and its refracted ray make with the normal, respectively.

From the formula the minimum refractive index is

$$\begin{gathered} {\mathrm{\mu }}_{\mathrm{m} }= \frac{\sin \mathrm{i}}{\sin \mathrm{r}} =\frac{\sin {90}^{\mathrm{o}}}{\sin {45}^{\mathrm{o}}} \\ =\frac{1}{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.} }=\sqrt{2} =1.414 \\ {\mathbf{\mu }}_{\mathbf{m}}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{1}\mathbf{.}\mathbf{4} \end{gathered}$$

A.

15 cm (Concave)

A concave lens is required by the person so that the lens forms the image of object distant 30 cm, at 10 cm it means.

$$\begin{gathered} \mathrm{u} = -30 \mathrm{cm}, \mathrm{\nu } = -10 \mathrm{cm} \\ \frac{1}{\mathrm{f}}= \frac{1}{\mathrm{\nu }} - \frac{1}{\mathrm{u}} \\ =\frac{1}{-10} - \frac{1}{-30} \\ =-\frac{2}{30} \\ \mathrm{or} \frac{1}{\mathrm{f}} =\frac{-1}{15} \\ \mathrm{Minus} \mathrm{sign} \mathrm{signifies} \mathrm{that} \mathrm{lens} \mathrm{used} \mathrm{is} \mathrm{concave}. \end{gathered}$$

B.

$\frac{1}{800}$

Ratio of time 

$$\begin{gathered} \frac{{\mathrm{t}}_1}{{\mathrm{t}}_2} ={\left(\frac{{\mathrm{f}}_1}{{\mathrm{f}}_2}\right)}^2 \\ ={\left(\frac{5\mathrm{f}}{2.5 \mathrm{f}}\right)}^2 \\ \Rightarrow \frac{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$200$}\right.}}{{\mathrm{t}}_2} ={\left(2\right)}^2 \\ \Rightarrow {\mathrm{t}}_2 = \frac{1}{800}\mathrm{s} \end{gathered}$$

D.

-0.75 D

f₁ = +80 cm, f₂ = -50 cm

Resultant focal length 

$$\begin{gathered} \mathrm{F} = \frac{{\mathrm{f}}_1{\mathrm{f}}_2}{{\mathrm{f}}_1 +{\mathrm{f}}_2} \\ =\frac{80 \times \left(-50\right)}{80 - 50} \\ = \frac{-4000}{30} \\ \mathrm{F} = -\frac{4000}{30}\mathrm{cm} \\ \mathrm{Resultant} \mathrm{power} \mathrm{P} = \frac{100}{\mathrm{F}} \\ = \frac{100}{-400/3} \\ = -3/4 \\ = -0.75 \mathrm{D} \end{gathered}$$

A.

red

Refractive index :- The extent of bending of light rays entering from one medium to another is known as  "Refractive index".

$\mathrm{\mu } = \frac{\mathrm{real} \mathrm{depth}}{\mathrm{apparent} \mathrm{depth}}$

For red colour, the refractive index is minimum, i.e it will have maximum apparent depth and hence, appears least raised.

D.

full image is seen and of decreased intensity

If half of the lens is covered with an opaque object, then, full image is seen but intensity of image decreases.

B.

2 × 10^-11 s

Time taken by light

$$\begin{gathered} \mathrm{t} = \frac{\mathrm{\mu } \mathrm{d}}{\mathrm{c}} \\ =\frac{1.5 \times 4 \times {10}^{-3}}{3 \times {10}^8} \\ = 2 \times {10}^{-11} \end{gathered}$$

B.

below 1.33

When lens is immersed in water then its nature changes. The refractive index of lens is less than that of water i.e.less than 1.33.

D.

10^-6 rad

Angular resolution describes the ability of any image forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution.$$\begin{gathered} \mathrm{Angular} \mathrm{resolution} = \frac{1.22 \mathrm{\lambda }}{\mathrm{d}} \\ = \frac{1.22 \times 5000 \times {10}^{-10}}{10 \times {10}^{-2}} \\ = 6.1 \times {10}^{-6} \\ \mathrm{Angular} \mathrm{resolution} = {10}^{-6} \mathrm{rad} \end{gathered}$$

C.

3.00

Velocity of light waves in material is 

ν = v λ                    ....(i)

Refractive index of material

$\mathrm{\mu } = \frac{\mathrm{c}}{\mathrm{\nu }} ....\left(\mathrm{ii}\right)$ 

where c is speed of light in vacuum or air

$\Rightarrow \mathrm{\mu } = \frac{\mathrm{c}}{\mathrm{v} \mathrm{\lambda }} ....\left(\mathrm{iii}\right)$

Given:-  v = 2 × 10¹⁴ Hz

λ = 5000 A^o

 λ = 5000 × 10^-10 m

c = 3 × 10⁸ m/s

Hence, from Eq. (iii), we get

$\mathrm{\mu } = \frac{3 \times {10}^8}{2 \times {10}^{14} \times 5000 \times {10}^{-10}}$

μ = 3.00

D.

D₁ > D₂

D = (μ - 1) A

For blue light μ is greater than that for red light, so D₂ > D₁

D.

L₄ , L₁

Length of tube = 10 cm

            f_o + f_e = 10 cm

Momentum m = $\frac{{\mathrm{f}}_{\mathrm{o}}}{{\mathrm{f}}_{\mathrm{e}}} = 4$

             f_o   = 4 f_e

Putting in eqⁿ (i),

            5f_e = 10 cm

⇒            f_e  = 2 cm

       and f_o = 8 cm

⇒            f_o = 8 cm, f_e = 2 cm

Hence L₄ and L₁ will be used.

A.

2D

Biconvex lens is cut perpendicularly to the principal axis, it will become plano-convex lens.
Focal length of biconvex lens

$$\begin{gathered} \frac{1}{\mathrm{f}} = \left(\mathrm{n} - 1\right) \left(\frac{1}{{\mathrm{R}}_1} - \frac{1}{{\mathrm{R}}_2}\right) \\ \frac{1}{\mathrm{f}} = \left(\mathrm{n} - 1\right) \frac{2}{\mathrm{R}} \\ \left( \because {\mathrm{R}}_1 = \mathrm{R}, {\mathrm{R}}_2 =-\mathrm{R}\right) \end{gathered}$$

$\Rightarrow \mathrm{f} = \frac{1}{2\left(\mathrm{n} - 1\right)} .... \left(\mathrm{i}\right)$

For plano-convex lens

$$\begin{gathered} \frac{1}{{\mathrm{f}}_1} = \left(\mathrm{n} - 1\right)\left(\frac{1}{\mathrm{R}} - \frac{1}{\infty }\right) \\ {\mathrm{f}}_1 =\frac{\mathrm{R}}{\left(\mathrm{n} - 1\right)} .....\left(\mathrm{ii}\right) \end{gathered}$$

Comparing Eqs. (i) and (ii), we see that focal length becomes double

As power of lens P  ∝ $\frac{1}{\mathrm{focal} \mathrm{length}}$

Hence, power will become half.

New power =$\frac{4}{2}$

New power = 2D

C.

the speed is different

When a ray of light travels from one medium to the second medium, it bends. If first medium is rarer and second medium is denser, it bends towards the normal while if first medium is denser and second medium is rarer, it bends away from the normal. This bending is due to refractive index of second medium with respect to first.

The refractive index is related to the speed of light in the two media as below

${}_1\mathrm{\mu }_2 = \frac{\mathrm{speed} \mathrm{of} \mathrm{light} \mathrm{in} \mathrm{first} \mathrm{medium}}{\mathrm{speed} \mathrm{of} \mathrm{light} \mathrm{in} \mathrm{second} \mathrm{medium}}$

(or)  speed of light in second medium = $\frac{\mathrm{speed} \mathrm{of} \mathrm{light} \mathrm{in} \mathrm{first} \mathrm{medium}}{{}_1\mathrm{\mu }_2}$

Where ₁μ₂ is refractive index of second medium relative to the first medium.

Hence, we see that on passing through another medium speed of light changes.

A.

40

In relaxed eye state of telescope or when final image is formed at infinity, the magnification of telescope is given by

             $\left|\mathrm{M}\right| = \frac{{\mathrm{f}}_{\mathrm{o}}}{{\mathrm{f}}_{\mathrm{e}}}$

where f_o = focal length of objective = 200 cm
f_e = focal length of eye-piece = 5 cm

hence       $\left|\mathrm{M}\right| = \frac{200}{5}$

                       = 40

Note:- The aperture of the objective lens is kept large so that more and more rays coming from the heavenly body may enter the telescope and a bright image is formed by the objective lens. The aperture of the eye lens is kept comparatively small so that all the rays may enter the eye.

A.

Two images are formed

Since, lens is made of two layers of different refractive indices, for a given wavelength of light it will have two focal lengths or will form two images at two different points as there are μ's is

                $\frac{1}{\mathrm{f}} \propto \left(\mathrm{\mu } - 1\right)$ 

C.

+1

In a plane mirror, the image formed is erect and of same size as of object. Thus, magnification of plane mirror is 1.

C.

Phase changes by 90°

When a ray of light moves from one medium to other, its velocity changes. This change depends on refractive index of the medium. 

Light travels from denser to rarer medium, ie, from medium of higher. refractive index to lower 
refractive mdex. So, in second (rarer) medium, its velocity increases.

B.

0.20 m

Let as shown, 1 and 2 are positions of objects and
images in two different situations.

It is given

               $\left|\frac{{\mathrm{v}}_1}{{\mathrm{u}}_1}\right| = 2 \left|\frac{{\mathrm{v}}_2}{{\mathrm{u}}_2}\right|$

Here, u₁ = -15 cm, u₂= -20 cm

                  ${\mathrm{v}}_1 = 2 {\mathrm{v}}_2 \times \frac{{\mathrm{u}}_1}{{\mathrm{u}}_2}$

                      = $2 {\mathrm{v}}_2 \times \frac{15}{20}$

                   ${\mathrm{v}}_1 = \frac{3}{2} {\mathrm{v}}_2$

Now,           $\frac{1}{\mathrm{f}} = \frac{1}{\mathrm{v}} - \frac{1}{\mathrm{u}}$

                  $\frac{1}{\mathrm{f}} = \frac{1}{{\mathrm{v}}_1} - \frac{1}{{\mathrm{u}}_1}$

                  $\frac{1}{\mathrm{f}} = \frac{1}{{\mathrm{v}}_2}- \frac{1}{{\mathrm{u}}_2}$

So,        $\frac{1}{{\mathrm{v}}_1} - \frac{1}{{\mathrm{u}}_1} = \frac{1}{{\mathrm{v}}_2} - \frac{1}{{\mathrm{u}}_2}$

⇒           $\frac{2}{3{\mathrm{v}}_2} + \frac{1}{15} = \frac{1}{{\mathrm{v}}_2}+\frac{1}{20}$

⇒                        v = 20 cm

⇒                         v = 0.20 m

D.

sum of the product of their powers and dispersive power equal to zero

The two lenses of an achromatic doublet should have, sum of the product of their powers and dispersive power equal to zero.

C.

50 cm

Using the formula

          $\frac{1}{\mathrm{v}} - \frac{1}{\mathrm{u}} = \frac{1}{\mathrm{f}}$

           $\frac{1}{\mathrm{v}} - \frac{1}{-30} = \frac{1}{20}$

          v = 60 cm

If the image is formed at the centre of curvature of the mirror, the coincidence is possible. Then the rays refracting through the lens will fall normally on the convex mirror and retrace their path of form the image at 0. Hence, the distance between lens and mirror will be

           60 - 10 = 50 cm

A.

6 m

Given:- μ = 5/3

      sin i = $\frac{1}{\mathrm{\mu }} = \frac{3}{5}$

      tan i =$\frac{\mathrm{r}}{4}$                  .... (tani = 3/4)

       tan i = $\frac{3}{4} \times 4$

It gives r = 3 m

So the diameter = 2 r

                       = 6 m

B.

90^o

Number of images = $\left(\frac{{360}^{\mathrm{o}}}{\mathrm{\theta }} - 1\right)$      

              n = $\frac{{360}^{\mathrm{o}}}{\mathrm{\theta }} - 1$

              3 = $\frac{{360}^{\mathrm{o}}}{\mathrm{\theta }} - 1$

               θ = 90^o 

C.

$\frac{\mathrm{t} \left({\mathrm{n}}_1 + {\mathrm{n}}_2\right)}{2 {\mathrm{n}}_1 {\mathrm{n}}_2}$

The apparent depth is given by

           I' = $\frac{{\mathrm{t}}_1}{{\mathrm{n}}_1} + \frac{{\mathrm{t}}_2}{{\mathrm{n}}_2}$

               = $\frac{{\displaystyle \raisebox{1ex}{$\mathrm{t}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{\mathrm{n}}_1} + \frac{{\displaystyle \raisebox{1ex}{$\mathrm{t}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{\mathrm{n}}_2}$

           I' = $\frac{\mathrm{t} \left( {\mathrm{n}}_1 + {\mathrm{n}}_2 \right)}{2 {\mathrm{n}}_1 {\mathrm{n}}_2}$

C.

6 m/s

     Velocity of bird w.r t. fish

        ${\mathrm{v}}_{ \mathrm{B}\to \mathrm{F}}$ = 10 m/s

   and velocity of fish w.r.t. ground

       ${\mathrm{v}}_{\mathrm{B}\to \mathrm{G}}$ = 2 m/s

∴   Distance between bird and fish, as seen by fish

       S = x + ny

on differentiating w.r.t. time, we get

       $\frac{\mathrm{dS}}{\mathrm{dt}} = \frac{\mathrm{dx}}{\mathrm{dt}} + \mathrm{n} \frac{\mathrm{dy}}{\mathrm{dt}}$

⇒     10 = 2 + $\frac{4}{3}$${\mathrm{v}}_{\mathrm{B}\to \mathrm{G}}$

⇒      ${\mathrm{v}}_{\mathrm{B}\to \mathrm{G}}$ = ${\mathrm{v}}_{\mathrm{F}\to \mathrm{G}} + \mathrm{n} . {\mathrm{v}}_{\mathrm{B}\to \mathrm{G}}$

⇒      10 = 2 + $\frac{4}{3} {\mathrm{v}}_{\mathrm{B}\to \mathrm{G}}$

⇒       ${\mathrm{v}}_{\mathrm{B}\to \mathrm{G}}$ = $\frac{8}{{\displaystyle \raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}$

⇒       ${\mathrm{v}}_{\mathrm{B}\to \mathrm{G}}$= 6m/s

D.

4 cm²

Given:-

    square wire of side= 2 cm

    u = $-$ 20 cm

    f = $-$10 cm

Area of second wire = ?

∴   $\frac{1}{\mathrm{v}} + \frac{1}{\mathrm{u}} = \frac{1}{\mathrm{f}}$

     $\frac{1}{\mathrm{v}} + \frac{1}{\left(-20\right)} = \frac{1}{-10}$

      $\frac{1}{\mathrm{v}} = -\frac{1}{10} + \frac{1}{20}$

        v = -20 cm

We know that,

       m = $-\frac{\mathrm{v}}{\mathrm{u}}$

           = $\frac{- \left(-20\right)}{-20}$

    m = -1

     $\frac{\mathrm{Area} \mathrm{of} \mathrm{image}}{\mathrm{Area} \mathrm{of} \mathrm{object}}$  = m²

        ^{$\frac{{\mathrm{A}}_{\mathrm{i}}}{{\mathrm{A}}_{\mathrm{o}}}= {\left(-1\right)}^2$}

      ^{$\frac{{\mathrm{A}}_{\mathrm{i}}}{2 \times 2} = 1$}

      A_i = 4 cm²

C.

$\frac{4}{3}$

  Refraction at plane surface (1)

   n₁ = 1,

 n₂ = 1.5 = $\frac{3}{2}$

  u = - mR

  v =?

Using formula,

          $\frac{{\mathrm{n}}_2}{\mathrm{v}} - \frac{{\mathrm{n}}_1}{\mathrm{u}} = \frac{{\mathrm{n}}_2 - {\mathrm{n}}_1}{\mathrm{R}}$

  since        R = ∞

   n₁ =  $\frac{3}{2}$, n₂ = 1

     $\frac{1}{\infty } - \frac{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\left[-\left({\displaystyle \frac{3}{2}} \mathrm{mR} + \mathrm{R}\right)\right]} = \frac{1 - {\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{-\mathrm{R}}$

⇒     $\frac{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{\displaystyle \frac{\mathrm{R} \left(3\mathrm{m} + 2\right)}{2}}} = \frac{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\mathrm{R}}$

⇒     $\frac{6}{3 \mathrm{m} + 2} = 1$

⇒       m = $\frac{4}{3}$

B.

1.42

Given:-

    λ₁ = 6000 A^o

     λ₂ = ?

Angular width of central maximum = $\frac{2 \mathrm{\lambda }}{\mathrm{a}}$

       θ₁ = $\frac{2 {\mathrm{\lambda }}_1}{\mathrm{a}}$                     .....(i)

and   θ₂ = $\frac{2 {\mathrm{\lambda }}_2}{\mathrm{a}}$

$\because$       θ₂ = θ₁ × 0.7

∴         θ₁ × 0.7 = $\frac{2 {\mathrm{\lambda }}_2}{\mathrm{a}}$           .....(ii)

From Eqs. (i) and (ii), we get

          $\frac{1}{0.7} = \frac{{\mathrm{\lambda }}_1}{{\mathrm{\lambda }}_2}$

⇒       λ₂ = λ₂ × 0.7

               = 4200 A^o

When immersed in liquid,

          ${\mathrm{\lambda }}_2 = \frac{{\mathrm{\lambda }}_1}{\mathrm{\mu }}$

$\because$      θ₂ = θ₁ × 0.7                      

⇒       $\frac{2 {\mathrm{\lambda }}_2}{\mathrm{a}} = \frac{2 {\mathrm{\lambda }}_1}{\mathrm{a}} \times 0.7$                             $\left[{\mathrm{\lambda }}_2 = \frac{{\mathrm{\lambda }}_1}{\mathrm{\mu }}\right]$ 

⇒      $\frac{2{\displaystyle \raisebox{1ex}{$ {\mathrm{\lambda }}_1 $}\!\left/ \!\raisebox{-1ex}{$\mathrm{\mu }$}\right.}}{\mathrm{a}} = \frac{2 {\mathrm{\lambda }}_1}{\mathrm{a}} \times 0.7$

⇒       $\frac{1}{\mathrm{\mu }}$ = 0.7

⇒        μ = 1.42