Obtain the mirror formula and write the expression for the linear magnification.

A relationship among the object distance (u), the image distance (v) and the focal length (f) of a mirror are called the mirror formula.

The formula is given by $\frac{1}{\mathrm{f}} = \frac{1}{\mathrm{u}} +\frac{1}{\mathrm{v}}$

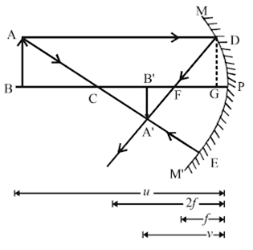
Take an object AB beyond C of a concave mirror MM'. A ray AD parallel to principal axis passes through focus after reflection.

Another ray AE which is passing through C comes back along the same path after reflection. 

These two reflected rays intersect at A'. A' draw perpendicular A'B' on the principal axis. So A'B' is a real and inverted image which is formed between C and F which is smaller than the object in size.

Draw DG perpendicular to the principal axis. So, applying sign convention, we get

PB = - u,

PB' = -v

PF = -f

PC = -2f

Now, In △ABC and △A'B'C, ∠ABC =∠A'B'C = 90°

∠ACB = ∠A'CB' (Vertically Opposite angles)
∴ △ABC ~△A'B'C (AA similarity)

$\frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}} = \frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}\text{'}}$ (the corresponding side of similar triangles are in proportion)..... (1)

In △DGF and △A'B'F, ∠DGF = ∠A'B'F = 90°

∠DGF= ∠A'FB' (vertically opposite angles)

△DGF ~△A'B'F (AA similarity)

$\frac{\mathrm{DG}}{\mathrm{A}\text{'}\mathrm{B}\text{'}} = \frac{\mathrm{GF}}{\mathrm{B}\text{'}\mathrm{F}\text{'}}$(corresponding sides of similar triangles are in proportion)

But AB = DG (the perpendicular distance between two parallel lines are equal)

$$\begin{gathered} \therefore \frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}} = \frac{\mathrm{GF}}{\mathrm{B}\text{'}\mathrm{F}\text{'}}.... \left(2\right) \\ \mathrm{From} \mathrm{eq} \left(1\right) \mathrm{and} \left(2\right), \mathrm{we} \mathrm{get}, \\ \frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}} = \frac{\mathrm{GF}}{\mathrm{B}\text{'}\mathrm{F}} ... \left(3\right) \end{gathered}$$

Let us assume the mirror is very small,

∴ G and P are very close to each other so that GF = PF.

From equation (3),

$$\begin{gathered} \frac{\mathrm{BC}}{\mathrm{B}\text{'}\mathrm{C}} = \frac{\mathrm{PF}}{\mathrm{B}\text{'}\mathrm{F}} \\ \Rightarrow \frac{\mathrm{PB} - \mathrm{PC}}{\mathrm{PC} - \mathrm{PB}\text{'}} \\ = \frac{\mathrm{PF}}{\mathrm{PB}\text{'} - \mathrm{PF}} \\ \Rightarrow \frac{-\mathrm{u} -(-2\mathrm{f})}{-2\mathrm{f}- (-\mathrm{v})} = \frac{{\displaystyle -\mathrm{f}}}{-\mathrm{v}-(-\mathrm{f})} \\ \Rightarrow \frac{-\mathrm{u} + 2\mathrm{f}}{-2\mathrm{f} + \mathrm{v}} = \frac{-\mathrm{f}}{-\mathrm{v} +\mathrm{f}} \\ \Rightarrow (-\mathrm{v} +\mathrm{f})(-\mathrm{u} +2\mathrm{f}) \\ =-\mathrm{f}(-2\mathrm{f} +\mathrm{v}) \\ \Rightarrow \mathrm{vu} -2\mathrm{fv}-\mathrm{fu} + 2{\mathrm{f}}^2 \\ = 2{\mathrm{f}}^2 - \mathrm{fv} \\ \Rightarrow \mathrm{uv} = - \mathrm{fv} + 2\mathrm{f} \\ \mathrm{v} +\mathrm{fu} \\ \therefore \mathrm{uv} = \mathrm{vf} + \mathrm{uf} \\ \mathrm{Dividing} \mathrm{both} \mathrm{sides} \mathrm{by} \mathrm{uvf} \\ \frac{\mathrm{uv}}{\mathrm{uvf}} = \frac{\mathrm{vf}}{\mathrm{uvf}} + \frac{\mathrm{uf}}{\mathrm{uvf}} \\ \Rightarrow \frac{1}{\mathrm{f}} = \frac{1}{\mathrm{u}} + \frac{1}{\mathrm{v}} \end{gathered}$$

If the mirror is plane, the size of the image is always equal to the size of the object i.e., magnification is unity. But the case is different for a curved mirror. The size of the image is different from the size of the object in such a 'mirror'. The image may be greater or smaller in size than the object depending upon the nature of the mirror or the location of the object.

Let I and O be the size of the image and the object respectively. The ratio I/O is called magnification, and it is denoted by m.

Magnification, m = I/O = -v/u

This is called linear magnification.