Mathematics Chapter 12 Areas Related To Circles

Steps of Construction :
(i)     Draw AB = 5.6 cm
(ii)    At a draw an acute ∠BAX below base AB.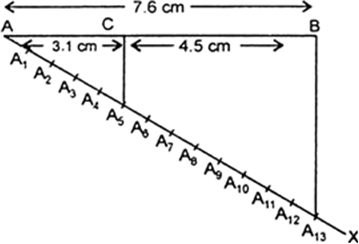

(iii)    On AX make 5 + 8 i.e. 13 equal parts and mark them as A₁, A₂, A₃, A₄,... A₁₃

(iv)    Join B to A₁₃. From A₅ draw A₅C || A₁₃B. C is the required point of division and AC : CB = 5 : 8.

On measuring, we get
AC = 3.1 cm,
CB = 4.5 cm
Justification :

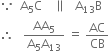
[Using basic proportionally theorem]

Therefore,    

This shows that C divides AB in the ratio 5 : 8.

(i) Construct a ΔABC in which AB = 6 cm, AC = 4 cm, BC = 5 cm.
(ii)    At A draw an acute ∠BAX below base AB.
(iii)    Along AX mark off points A₁, A₂, A₃ such that AA₁ = A₁ A₁ = A₂ A₃.
(iv)    Join A₃B.
(v)    From A₂ draw A₂B’ || A₃B meeting AB at B’.
(vi)    From B’ draw B‘C’ || CB meeting AC at C’. Thus, ΔAB‘C’ is the required triangle, each of whose sides is (2/3)rd of the corresponding sides of the ΔABC.
Justification :

[From (i)]
[By Basic proportionality theorem)

Steps of Construction :

(i)     Construct a ΔABC in which AB = 7cm, AC = 5 cm, BC = 6 cm.
(ii)    At A draw an acute ΔBAX below base AB.
(iii)   Along AX, mark off 7 points A₁, A₂, A₁,.,
A₇. Such that AA₁ = A₁ A₂ = A₂ A₃
= A₃ A₄ =......= A₆A₇.

(iv) Join A₅B.
(v) From A₇ draw A₇B’ || A₅B meeting produced part of AB at B’.
(vi) From B’, draw B‘C’ || BC intersecting the extended line segment AC at C’.
Thus, AB‘C’ is the required triangle each of whose sides is 7/5 of the corresponding sides of the triangle ΔABC.
Justification :

Step of Construction :

(i)    Draw a line segment BC = 8 cm.
(ii)   Draw a perpendicular bisector AD (4 cm) of BC.
(iii)  Joining AB and AC we get isosceles ΔABC.

(iv)    Construct an acute ∠CBX downwards.
(v)    Along BX mark off 3 equal points B₁, B₂, B₃ such that BB₁ = B₁B₂ = B₂B₃.
(vi)    Join C to B₂ and draw a line through B₃ parallel to B₂C intersecting the extended line segment BC at C’.
(vii)    Again draw a parallel line C’ A’ to AC cutting BP at A’.
(viii)    ΔA ‘BC’ is the required triangle.
Justification :
C’A’ || CA [By construction] ΔABC ~ ΔA ‘BC’
[Using AA similarity condition]

Steps of Construction :

(i)    Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
(ii)    Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
(iii)    Along BX, mark off 4 points B₁, B₂, B₃ and B₄ on BX such that BB₁ = B₁B₂ = B₂ B₃ = B₃B₄.
(iv) Join B₄C and draw a line through B₃ parallel to B₄ C intersecting BC to C’.
(v) Draw a line through C’ parallel to the line CA to intersect BA at A’.

Then A ‘BC’ is the required triangle. Justification :

[By the Basic Proportionality Theorem]

Steps of Construction :
(i) Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°.
(it) Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
(iii)    Along BX, mark off 4 points B₁, B₂, B₃ and B₄ on BX such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄
(iv)    Join B₃ to C and draw a line through B₄ parallel to B₃C, intersecting the extended line segment BC at C’.
(v) Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’.

Then A ‘BC’ is the required triangle. Justification :

Steps of Construction :
(i) Draw line BC = 4 cm.
(ii) Draw BA = 3 cm line segment with 90° at B.

(iii)    Join AC to form right ΔABC.
(iv)    Construct an acute ∠CBX downwards.
(v)    Along BX mark off 5 equal points B₁, B₂, B₃, B₄, B₅ such that BB₁ = B₁B₂=... = B₄B₅.
(vi)    Join C to B₃ and draw a line through B₅ parallel to B₃C intersecting the extended line segment BC at C’.
(vii)    Again we draw C’A’ parallel to AC.Thus, ΔA‘BC’ is the required triangle.
Justification :

Steps of Construction :
(i)    Construct a circle of radius 6 cm.
(ii)    Join PO and bisect it Let M be the midpoint of PO.
(iii)    Taking M as centre and MO as radius, draw a circle. Let it intersect the given circle at the points Q and R.
(iv)    Join PQ and PR.
(v)    PQ and PR are the required two tangents.
(vi)    PQ = PR = 8 cm.
Justification :
Join OQ and OR.
∵ ∠OQP and ∠ORP are the angles in semi circles.
∠OQP = 90° = ∠ORP
Also, since OQ, OR are radii of the circle, PQ and PR will be the tangents to the circle at Q and R respectively.

Steps of Construction :
(i)    Join PO and bisect it. Let M be the midpoint of PO.
(ii)    Taking Mas centre and MO as radius, draw a circle. Let it intersect the given circle at the point Q and R.
(iii)    Join PQ.
By measurement PQ = 4.5 cm
Then PQ is the required tangent.
By actual calculation,

Steps of Construction :
(i) Bisect PQ. Let M be the mid-point of PO.
(ii)    Taking M as centre and MO as radius, draw a circle which intersect the given circle at the points A and B.
(iii)    Join PA and PB.
Now, PA and PB are the required two tangents.
(iv)    Bisect QO. Let N be the mid-point of QO.
(v)    Taking N as centre and NO as radius, draw a circle. Let it intersect the given circle at the points C and D.
(vi)    Join QC and QD.

Then QC and QD are the required two tangents.
Justification : Join OA and OB.
Then ∠PAO is an angle in the semicircle and, therefore,
∠PAO = 90°
⇒    PA ⊥ OA
Since, OA is a radius of the given circle, PA has to be a tangent to the circle. Similarly, PB is also a tangent to the circle.
Again, Join OC and OD.
Then ∠QCO is an angle on the semicircle and therefore,
∠QCO = 90°
Since, OC is a radius of the given circle, QC has to be a tangent to the circle.
Similarly, QD is also a tangent to the circle.

Steps of Construction :

(i)    Take a point O on the plane of the paper and draw a circle of radius OA = 5 cm.
(ii)    Produce OA to B such that OA = AB = 5 cm.
(iii)    Taking A as the centre draw a circle of radius AO = AB = 5 cm.
(iv)    It cuts the circle at P and Q.
(v)    Join BP and BQ to get the desired tangents.

Justification :

In AOAP, we have
OA = OP = 5 cm (= Radius)
Also, AP = 5 cm (Radii of circle)
∴ ΔOAP is equilateral.
⇒ ∠PAO = 60°
⇒ ∠BAP = 120°
In ΔBAP, we have
BA = AP and ∠BAP = 120°
∴ ∠ABP = ∠APB = 30°
⇒ ∠PBQ = 60°

Steps of Construction :
(i) Draw a line segment AB = 8 cm.
(ii)    Draw a circle with centre A and radius 4 cm. Draw another circle with centre B and radius 3 cm.
(iii)    Let M be the mid-point of AB. Taking M as centre and AM as radius draw a circle which intersects the circles at P, Q, R and S.

Fig,
(iv) Join AP, AQ, BR and BS. These are required tangents.

Steps of Construction :
(i).    Draw line segments BC = 4 cm and AB = 3 cm perpendicular to each other. Join AC. ΔABC is the right triangle.
(ii)    Taking mid-point E of BC as centre, draw a circle with radius 2 cm, passing through B, C and D.
at B, i.e. AB ⊥ BC.
Its length AB = 3 cm.
Taking centre A, draw an arc of 3 cm (AB = AF) cutting the circle at F.
Join AF. AF and AB are the required tangents.

Steps of Construction :
(i)    Draw a circle with the help of bangle.
(ii)    Draw two chords AB and AC. Perpendi-cular bisectors of AB and AC intersect each other at O, which is the centre of the circle.

(iii)    Taking a point P outside the circle, join OP.
(iv)    Let M be the midpoint of OP. Taking M as centre and OM as radius draw a dotted circle which intersect the given circle at Q and R.
(v)    Join PQ and PR. Thus, PQ and PR are required tangents.

(i) Draw AB = 7.6 cm.
(ii)    Draw a ray AX making an acute ∠ BAX.
(iii)    Along AX, mark point A₁, A₂, A₃ ...., A₈, Such that AA₁ = A₁A₂ = .......= A₇ A₈.(iv)    Join A₈ B.
(v)    Through A₃, draw a line A₃C || A₈B intersecting AB at C.
Thus, point so obtained is the required point which divides AB internally in the ratio 3 : 5.

(i) Draw AB = 6 cm.
(ii) Draw a ray AX making an acute ∠ BAX.
(iii) Along AX, mark points A₁, A₂, A₃ ..., A₇, such that AA₁ = A₁A₂.........= A₆A₇.
(iv)    Join A₇B.
(v)    Through A₃ draw a line A₃C ||A₇B intersecting AB at C.
Thus, points C so obtained is the required point which divides internally in the ratio 3 : 4.

(i)    Draw AB =11 cm.
(ii)    Draw a ray AX making an acute ∠ BAX.
(iii)    Along AX, mark points A₁, A₂, A₃ .........,
A₇. Such that AA_l = A₁A₂ = .......= A₆A₇.
(iv)    Join A₇ B.
(v) Through A₂, draw a line A₂C || A₇B intersecting AB at C.
Thus, point C so obtained is the required point which divides AB internally in the ratio 2
: 5.
(b) Externally : Steps of Construction
(i)    Draw AB = 11 cm.
(ii)    Draw a ray BX making an acute ∠ ABX.
(iii)    Along a ray BX, mark points B₁, B₂,..., B₅, such that BB₁ = B₁B₂ = B₂B₃ =
B₃B₄= B₄B₅.

(iv) Join B₃A.
(v) Through B₅, draw a line parallel to B₃A intersecting BA produced at C.
Thus, point C so obtained is the required point which divides AB externally in the ratio 2 : 5.
Constructions Based on similar triangle

Steps of Construction :

(i)    Draw a line segment AB = 5 cm.
(ii)    Draw ∠ABX = 60°.
(iii)    Draw AM ⊥ AB at A.
(iv)    Draw NT ⊥ AM cutting BX at C.
(v)    Join AC.
Now, ABC is the required triangle.
Construction of another triangle AQR similar to ΔABC.
Steps of Construction :
(i) Produce AB to Q such that

Steps of Construction :

(i)    Construct a ΔPQR in which PR = PQ = 5 cm and QR = 6cm.
(ii)    At P draw an acute ∠QPX, below base PQ.
(iii)    Along PX, mark off
P₁, P₂, P₃,..., P₆,P₇.
(iv)    Join P₇Q.
(v)    From P₅ draw P₅B || P₇Q meeting PQ at B.
(vi)    From B, draw BC || RQ meeting PR at C.
Thus ΔPBC is the required triangle, each of whose sides is  of the corresponding sides of the ΔPQR.

Steps of Construction :

(i)    Construct a triangle ABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm.
(ii)    At B draw an acute ∠CBX below base BC.
(iii)    Along BX, mark off points B₁, B₂, B₃, B₄, such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
(iv)    Join B₄C.
(v) From B₃ draw B₃C’ || B₄C meeting BC at C’.
(vi) From C’ draw C’ A’ || CA, meeting AB at A’. Thus A ‘BC’ is the required triangle each of whose sides is 3 / 4th of the corresponding sides of ΔABC

Steps of Construction:
(i)     Draw a line segment BC = 6 cm.
(ii)    Draw a ray BX making an angle 60° with BC.

(iii)    Through B, draw MB ⊥ BX.
(iv)    Draw perpendicular bisector of BC which intersects BC at D and MB at O.
(v) With O as centre and OB as radius draw a circle.
(vi)    With D as centre and 4.5 cm as radius, draw an arc which intersects the circle at A.
(vii)    Join AB and AC. ΔABC is the required triangle.
(viii)    Produce BC to C’, such that BC’ = 8 cm.
(ix) Through C’, draw C’A || CA which meets BA produced at A’.
Thus A’ BC’ is the required triangle similar to triangle ABC.

Steps of Construction :
1.    Draw a line segment AB = 5 cm.
2.    At A make ∠BAY = 45°.
3.    Take A as centre and radius = AC = 6 cm (= CA), draw an arc cutting AY at C.
4.    Join BC to obtain the triangle ABC.
5.    Draw any ray AX making an acute angle with AB on the side opposite to the vertex
C.
6.    Mark off 6 points (the greater of 6 and 5 in 6/5) A₁, A₁, A₃, A₄,A₅ and A₆ on AX so
that
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆
7.    Join A₅ (the 5th point, being the smaller of 5 and 6 in 5/6) to B and draw a line through A₆ parallel to A₅B intersecting the extended line segment AB at B’.
8.    Draw a line through B‘C’ parallel to BC intersecting the extended line segment AC at C’.
Thus, AB ‘C’ is the required triangle

Steps of Construction :

1.    Draw a line segment BC = 6 cm.
2.    At B make ∠CBY = 60°.
3.    Take B as centre and radius = AB = 4 cm, draw an arc cutting BY at A.
4.    Join CA to obtain the triangle ABC.
5.    Draw any ray BX making an acute angle with BC on the opposite side of the vertex A.
6.    Mark off 4 (the greater of 3 and 4 in 3/ 4) points B₁, B₂, B₃ and B₄ on BX so that
BB₁ = B₁B₂ = B₂B₃ = B₃B₄

7.    Join B₄C and draw a line through B₃ (the third point, 3 being smaller of 3 and 4 in 3/4), parallel to B₄C to intersect BC at C’.
8.    Draw a line through C’ parallel to the line CA to intersect BA at A’ (see Fig.) Thus, ΔA ‘BC’ is the required triangle.

Steps of Construction:

(i) Construct a ΔABC in which AB = 6.5 cm, ∠B = 60°, BC = 5.5 cm.
(ii)    At B draw an acute angle CBX below base BC.
(iii)    Along BX, mark off points B₁, B₂, B₃, such that BB₁ = B₁ B₂ = B₂ B₃.
(iv)    Join B₂C.
(v)    From B₃ draw B₃C’ || B₂C meeting produced part of BC at C.
(vi)    From C’, draw C’ A’ || C    A intersecting the extended line segment BA at A’.

Thus, A’B’C’ is the required triangle each of whose sides is 3/2 times the corresponding sides of the triangle ΔABC.

Construction Based on tangent to a circle

Steps of Construction :

(i) Construct a circle C₁ (say) of radius 3 cm.
(ii)    P is a point 5 cm away from the centre of circle C₁.
(iii)    Join OP.
(iv)    Draw ⊥ bisector of OP which intersects OP at M.

(v)    Taking M as centre and OM as radius draw a circle which intersects the circle C₁at A and B.
(vi)    Join PA and PB
(vii)    On, measuring we find PA = PB = 4 cm. Thus PA and PB are the required tangents.

Steps of Construction :

(i) Take a point O in the plane of the paper and draw a circle of radius 4 cm.
(ii) Mark a point P at a distance of 6 cm from the centre O and join OP.
(iii)    Bisect the line segment OP. Let the point of bisection be M.
(iv)    Taking M as centre and OM as radius, draw a circle to intersect the given circle at the points T and T’.
(v) Join PT and PT’ to gel the required tangents.

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Sollution not provided.   

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.                                             

Solution not provided.                                             

Solution not provided.   

Solution not provided.   

Solution not provided.

Solution not provided. 

Solution not  provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided. 

Solution not provided.

Solution not provided. 

Solution not provided.

Solution not provided. 

Solution not  provided.

Solution not  provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided. 

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Solution not provided.

Steps of construction:
(i) Take a point O on the plane of the paper and draw a circle of radius OA = 4 cm.
(ii) Produce OA to B such that OA = AB = 4 cm.
(iii) Draw a circle with centre at A and radius AB.
(iv) Suppose it cuts the circle drawn in step (i) at P and Q.
(v) Join BP and BQ to get the desired tangents.

Justification:
In ΔOAP, OA = OP = 4 cm ...(radii of the same circle)
Also, AP = 4 cm ….(Radius of the circle with centre A)

∴ ΔOAP is equilateral.
∠PAO = 60^o
∴ ∠BAP = 120^o
In ΔBAP, we have BA = AP and ∠ BAP = 120^o
 ∴∠ABP = ∠APB = 30^o
Similarly we can get ∠ABQ = 30^o
∴ ∠PBQ = 60^o

Given: TP and TQ are two tangent drawn from an external point T to the circle C (O, r).


To prove: TP = TQ
Construction: Join OT
Proof: we know that a tangent to the circle is perpendicular to the radius through the point of contanct.
∴ ∠OPT = ∠OQT = 90^o
In Δ OPT  and ΔOQT
OT = OT  (common)
OP = OQ (radius of the circle)
∠OPT = ∠OQT (90^o)
∴ ∠OPT = ∠OQT (RHS congruence criterion)
⇒ TP = TQ (CPCT)
Hence, the length of the tangents drawn from an external point to a circle is equal.

Scale factor 
The required triangle can be drawn using the following steps:
1. Draw  a ΔABC with side AB = 6 cm, ∠A = 30^o and ∠B = 60^o.
2. Draw a ray AZ making an acute angle with AB on the opposite side of vertex C.
3. Locate 4 points ( as 4 is greater in 4 and 3) A₁, A₂, A₃, and A₄ on AZ.
4. Join A₃B. Draw a line through A₄ parallel to A₃B intersecting extended AB at B^'.
5. Through B^', drawn a line parallel to BC intersecting ray AX at C'.
Hence, ΔAB'C' is the required triangle.

$$\begin{gathered} \mathrm{AB} \mathrm{and} \mathrm{CD}\hspace{0.17em}\mathrm{are} \mathrm{the} \mathrm{diameters} \mathrm{of} \mathrm{a} \mathrm{circle} \mathrm{with} \mathrm{centre} \mathrm{O}. \\ \therefore \mathrm{OA} = \mathrm{OB} = \mathrm{OC} =7 \mathrm{cm} ( \mathrm{Radius} \mathrm{of} \mathrm{the} \mathrm{circle}) \\ \mathrm{Area} \mathrm{of} \mathrm{the} \mathrm{shaded} \mathrm{region} = \\ = \mathrm{Area} \mathrm{of} \mathrm{the} \mathrm{circle} \mathrm{with} \mathrm{diameter} \mathrm{OB} + ( \mathrm{Area} \mathrm{of} \mathrm{the} \mathrm{semi}-\mathrm{circle} \mathrm{ACDA} - \mathrm{Area} \\ \mathrm{of} ∆\mathrm{ACD} ) \\ =\mathrm{\pi } {\left(\frac{7}{2}\right)}^2 + \left( \frac{1}{2} \mathrm{x} \mathrm{\pi } \mathrm{x} 7^2 - \frac{1}{2} \mathrm{x} \mathrm{CD} \mathrm{x} \mathrm{OA}\right) \\ = \frac{22}{7} \mathrm{x} \frac{49}{4} + \frac{1}{2} \mathrm{x} \frac{22}{7} \mathrm{x} 49 - \frac{1}{2} \mathrm{x} 14 \mathrm{x} 7 \\ = \frac{77}{2} + 77- 49 \\ = 66.5 {\mathrm{cm}}^2 \end{gathered}$$

  $$\begin{gathered} \mathrm{Area} \mathrm{of} \mathrm{a} \mathrm{trapezium} = 24.5 {\mathrm{cm}}^2 \\ \frac{1}{2} \left[\mathrm{AD} + \mathrm{BC}\right] \mathrm{X} \mathrm{AB} = 24.5 {\mathrm{Cm}}^2 \\ \frac{1}{2} \left[10+4\right] \mathrm{X} \mathrm{AB} = 24.5 \\ \mathrm{AB} = 3.5 \mathrm{cm} \\ \mathrm{r}= 3.5 \mathrm{cm} \\ \mathrm{Areao} \mathrm{of} \mathrm{quadrant} = \frac{1}{4}\mathrm{x} \mathrm{\pi } {\mathrm{r}}^2 \\ = 0.25 \mathrm{x} \frac{22}{7} \mathrm{x} 3.5 \mathrm{x} 3.5 \\ = 9.625 {\mathrm{cm}}^2 \\ \mathrm{The} \mathrm{area} \mathrm{of} \mathrm{shaded} \mathrm{region} = 24. 5 - 9.625 \\ = 14.875 {\mathrm{cm}}^2 \end{gathered}$$       

We have,

Area of the region ABCD

  = Area of the sector AOB - Area of the sector COD

 $$\begin{gathered} = \left(\frac{60}{360} \mathrm{x} \frac{22}{7} \mathrm{x} 42 \mathrm{x} 42 - \frac{60}{360} \mathrm{x} \frac{22}{7} \mathrm{x} 21 \mathrm{x} 21\right) {\mathrm{cm}}^2 \\ = \left(\frac{1}{6} \mathrm{x} 22 \mathrm{x} 6 \mathrm{x} 42 - \frac{1}{6} \mathrm{x} 22 \mathrm{x} 3 \mathrm{x} 21\right) {\mathrm{cm}}^2 \\ = \left(22 \mathrm{x} 42 - 11 \mathrm{x} 21\right) {\mathrm{cm}}^2 \\ = \left(924 - 231\right) {\mathrm{cm}}^2 \\ = 693 {\mathrm{cm}}^2 \\ \mathrm{Area} \mathrm{of} \mathrm{circular} \mathrm{ring} = \left(\frac{22}{7} \mathrm{x} 42 \mathrm{x}42 - \frac{22}{7} \mathrm{x} 21 \mathrm{x}21\right) {\mathrm{cm}}^2 \\ = \left(22 \mathrm{x} 6 \mathrm{x} 42 - 22 \mathrm{x} 3 \mathrm{x} 21\right) {\mathrm{cm}}^2 \\ = \left(5544 - 1386\right) {\mathrm{cm}}^2 \\ = 4158 {\mathrm{cm}}^2 \end{gathered}$$

Hence, Required shaded region = Area of circular ring - Area of region ABCD

                                             = (4158 - 693) cm²

                                             = 3465 cm²

AC = 24 cm,  AB = 7 cm

Since BC is the diameter of the circle,

$$\begin{gathered} \mathrm{So}, \angle \mathrm{BAC} = 90° \\ \mathrm{In} \mathrm{right} ∆\mathrm{BAC}, \\ {\mathrm{BC}}^2 = {\mathrm{AC}}^2 = {\mathrm{AB}}^2 \\ \Rightarrow {\mathrm{BC}}^2 = {24}^2 + 7^2 \\ \Rightarrow {\mathrm{BC}}^2 =625 \\ \Rightarrow \mathrm{BC} = 25 \\ \mathrm{So}, \mathrm{the} \mathrm{radius} \mathrm{of} \mathrm{the} \mathrm{circle} = \mathrm{OC} = 12.5 \mathrm{cm} \\ \mathrm{Area} \mathrm{of} \mathrm{the} \mathrm{shaded} \mathrm{region} \\ = \mathrm{Area} \mathrm{of} \mathrm{the} \mathrm{circle} - \mathrm{Area} \mathrm{of} ∆\mathrm{BAC} - \mathrm{Area} \mathrm{of} \mathrm{sector} \mathrm{CD} \\ = {\mathrm{\pi r}}^2 - \frac{1}{2} \mathrm{x} \mathrm{AB} \mathrm{X} \mathrm{AC} - \frac{\mathrm{\theta }}{360} \mathrm{X} {\mathrm{\pi r}}^2 \\ = \left(\frac{22}{7} \mathrm{x} 12.5 \mathrm{x} 12.5\right) - \left(\frac{1}{2} \mathrm{x} 7 \mathrm{x} 24\right) - \left(\frac{90}{360} \mathrm{x} \frac{22}{7} \mathrm{x} 12.5 \mathrm{x} 12.5\right) \\ ..........(\because \angle \mathrm{BOD} = 90° \Rightarrow \angle \mathrm{COD} = 90° ) \\ = 491.07 - 84 - 122.77 \\ = 284.3 {\mathrm{cm}}^2 ( \mathrm{approximately}) \\ \mathrm{Hence}, \mathrm{the} \mathrm{area} \mathrm{of} \mathrm{the} \mathrm{shaded} \mathrm{region} \mathrm{is} 284.3 {\mathrm{cm}}^2 \mathrm{approximately}. \end{gathered}$$

B.

26

Diameter of two circles are given as 10 cm and 24 cm.

Radius of one circle = r₁ = 5 cm,  Radius of other circle = r₂ = 12 cm.

According to the given information,

$$\begin{gathered} Area of the larger circle = \mathrm{\pi }({\mathrm{r}}_1{)}^2 + \mathrm{\pi }({\mathrm{r}}_2{)}^2 \\ = \mathrm{\pi }(5{)}^2 + \mathrm{\pi }(12{)}^2 \\ = \mathrm{\pi }(25 + 144) \\ = 169\mathrm{\pi } \\ = \mathrm{\pi }(13{)}^2 \end{gathered}$$

$\therefore$ Radius of the larger circle = 13 cm

Hence, the diameter of larger circle = 26 cm.

Given: OABC is a square  of side 7 cm

i.e. OA = AB = BC = OC = 7 cm

$\therefore$ Area of square OABC = ( side )² = 7² = 49 sq. cm.

Given, OAPC is a quadrant of a circle with centre O.

$\therefore$ Radius of the sector = OA = OC = 7 cm.

Sector angle = 90⁰

$$\begin{gathered} \therefore \mathrm{Area} \mathrm{of} \mathrm{quadrant} \mathrm{OAPC} = \frac{{90}^0}{{360}^0} \mathrm{x} {\mathrm{\pi r}}^2 \\ = \frac{1}{4} \mathrm{x} \frac{22}{7} \mathrm{x} 7 \mathrm{x} 7 \\ = \frac{77}{2} \mathrm{sq}.\mathrm{cm}. \\ = 38.5 \mathrm{sq}.\mathrm{cm}. \\ \therefore \mathrm{Area} \mathrm{of} \mathrm{shaded} \mathrm{portion} = \mathrm{Area} \mathrm{of} \mathrm{square} \mathrm{OABC} - \mathrm{Area} \mathrm{of} \mathrm{quadrant} \mathrm{OAPC} \\ = (49 - 38.5) \mathrm{sq}.\mathrm{cm}. \\ = 10.5 \mathrm{sq}.\mathrm{cm}. \end{gathered}$$

Area of the shaded region = Area of the sector POQ - Area of the sectos AOB

$$\begin{gathered} \mathrm{Area} \mathrm{of} \mathrm{shaded} \mathrm{region} = \left(\frac{\mathrm{\theta }}{360} \mathrm{\pi } {\mathrm{R}}^2 - \frac{\mathrm{\theta }}{360} \mathrm{\pi } {\mathrm{r}}^2 \right) \\ = \frac{\mathrm{\theta }}{360} \mathrm{\pi } \left( {\mathrm{R}}^2 - {\mathrm{r}}^2 \right) \\ = \frac{30}{360} \mathrm{x} \frac{22}{7} \mathrm{x} \left(7^2 - ( 3.5{)}^2\right) \\ = \frac{1}{12} \mathrm{x} \frac{22}{7} \mathrm{x} \left(49 - 12.25\right) \\ = \frac{22}{12 \mathrm{x} 7} \mathrm{x} 36.75 \\ = \frac{77}{8} {\mathrm{cm}}^2 \end{gathered}$$