Mathematics Chapter 10 Visualising Solid Shapes
Sponsor Area
NCERT Solution For Class 8 Social%2525252525252bscience
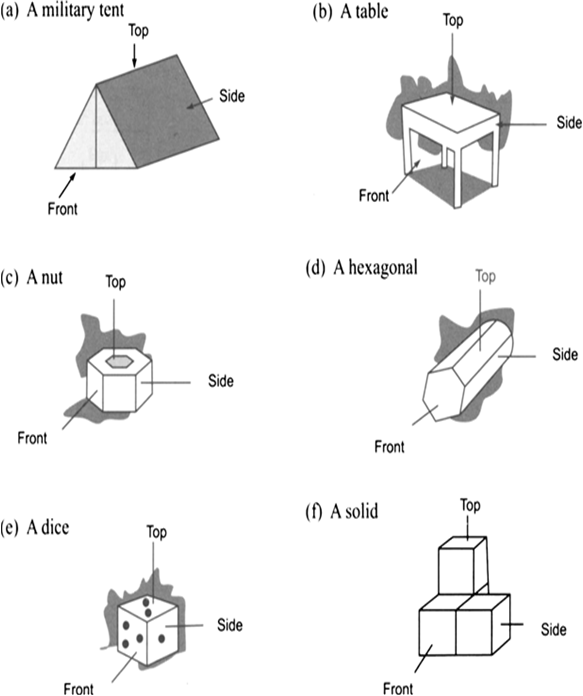
Let there be a combination of three cubes, one on the top of the other as shown in the adjoining figure. What will be its top and side view?

(ii) If we look at it from a side, i.e. left or right, then we would see a figure as shown here.
Note: In this case the front view would also be the same.
Look at the combination of four cubes as shown in the adjoining figure. Show its various views.

Look at the given map of a city.

Answer the following.
(a) Colour the map as follows: Blue-water, red-fire station, orange-library, yellow-schools. Green-park, Pink-College, Purple-Hospital, Brown-Cemetery.
(b) Mark a green ‘X’ at the intersection of Road ‘C’ and Nehru Road, Green ‘Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?
(a). Here various colours are as under


(b) Do as directed.
(c) Do as directed.
(d) City park.
(e) Senior Secondary school
Draw a map of your class using proper scale and symbols for different objects.
Draw a map of your school compound using proper scale and symbols for various features like play ground main building, garden, etc.
Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
What happens to F, V and E if some parts are sliced off from a solid? (To start with, you may take a plasticine cube, cut a corner off and investigate).
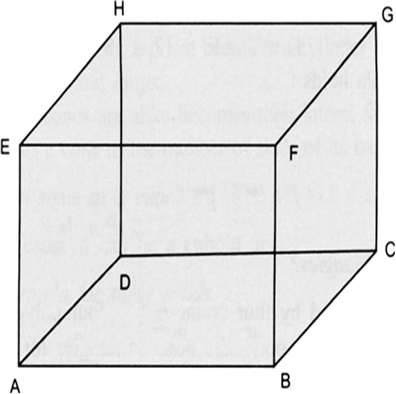
Case I: The given cuboid has:
(i) Number of faces (F) = 6
(ii) Number of vertices(V) = 8
(iii) Number of edges (E) = 12
We have, F + V = 6 + 8 = 14
F + V - E = 14 - 12 = 2
i.e. F + V - E = 2
or the Euler's formula is verified.
Case II: [A part is sliced off]
We have:
Number of faces (F) = 7
Number of vertices (V) = 10
Number of Edges (E) = 15
Also, F + V = 7 + 10 = 17
and F + V - E = 17 - 15 = 2
Here also, Euler's formula holds true.
Can a polyhedron have for its faces 3 triangles?
Sponsor Area
Can a polyhedron have for its faces 4 triangles?
Can a polyhedron have for its faces a square and four triangles?
Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid).
Which are prisms among the following?


Since, a prism is a polyhedron having two of its faces congruent and parallel, where as other faces are parallelogram.
∴ (i) No, a nail is not a prism.
(ii) Yes, unsharpened pencil is a prism.
(iii) No, table weight is not a prism.
(iv) Yes, box is a prism.
How are prisms and cylinders alike?
How are pyramids and cones alike?
Is a square prism same as a cube? Explain.
Verify Euler’s formula for these solids.

F = 7, V = 10 and E = 15
∴ F + V = 7 + 10 = 17
F + V - E = 17 - 15 = 2
i.e. F + V - E = 2
Thus, Euler's formula is verified.
(ii) In figure (ii), we have
F = 9, V = 9 and E = 16
∴ F + V = 9 + 9 = 18
and F + V - E = 18 - 16 = 2
i.e. F + V - E = 2
Thus, Euler's formula is verified.
Using Euler’s formula find the unknown.

Since F + V - E = 2
∴ F + 6 - 12 = 2
or F - 6 = 2
or F = 2 + 6 = 8
(ii) Here, F = 5 and E = 9
Since F + V - E = 2
or 5 + V - 9 = 2
or V - 4 = 2
or V = 2 + 4 = 6
(iii) Here F = 20 and V = 12
Since, F + V - E = 2
∴ 20 + 12 - E = 2
or 20 + 12 - E = 2
32 - E = 2
or E = 32 - 2 = 30
Can polyhedron have 10 faces, 20 edges and 15 vertices?
Here, F = 10, E = 20 and V = 15
We have:
F + V - E = 2
∴ 10 + 15 - 20 = 2
or 25 - 20 = 2
or 5 = 2 which is not true
i.e. ![]()
Thus, such a polyhedron is not possible.
Define the following:
(i) Polyhedron (ii) Prism (iii) Pyramid
(i) Polyhedron: A solid shapes bounded by polygons is called a polyhedron. For example, cube, cuboid, etc.
(ii) Prism: A prism is a solid, whose faces are parallelograms and whose ends (or bases) are congruent parallel rectilinear figures.
(iii) Pyramid: A pyramid is a polyhedron whose base is a polygon of any number of sides and whose other faces are triangles with a common vertex.
What is a tetrahedron?
What is a parallelopiped?
Which of the following solids are not polyhedrons?
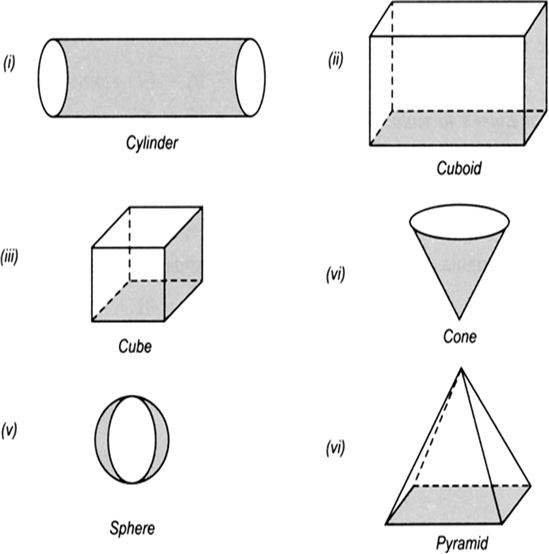
(i) A cylinder is not a polyhedron.
(ii) A cuboid is a polyhedron.
(iii) A cube is a polyhedron.
(iv) A cone is not a polyhedron.
(v) A sphere is not a polyhedron.
(vi) A pyramid is a polyhedron.
Why the following solids are not polyhedron?
(i) A sphere.
(ii) A cone.
(iii) A cylinder.
Name the following polyhedron.
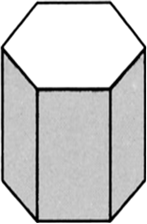
How many faces, vertiecs and edges of this solid are there?
∵ The ends (bases) of the given solid are congruent rectilinear figure each of six sides.
∴ It is a hexagonal prism.
In a hexagonal prism, we have:
The number of faces = 8
The number of edges = 18
The number of vertices = 12
Sponsor Area
What Euler’s formula? Verify the Euler’s formula for a pentagonal prism.
If a polyhedron is having number of faces as F, number of edges as E and the number of vertices as V, then the relationship F + V = E + 2 is known as Euler’s formula. Following figure is a solid pentagonal prism.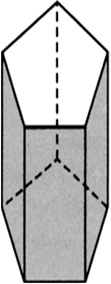
It has:
Number of faces (F) = 7
Number of edges (E) = 15
Number of vertices (V) = 10
Substituting the values of F, E and V in the relation,
F + V = E + 2
we have
7 + 10 = 15 + 2![]() 17 = 17
17 = 17
Which is true, the Euler’s formula is verified.
A polyhedron is having 8 vertices and 12 edges. How many faces of it are there?
Number of vertices (V) = 8
Number of edges (E) = 12
Let the number of faces = V
Now, using the Euler's formula
F + V = E + 2
we have
F + 8 = 12 + 2![]() F + 8 = 14
F + 8 = 14![]() F = 14 - 8
F = 14 - 8 ![]() F = 6
F = 6
Thus, the required number of faces = 6.
A dodecahedron is having 20 vertices and 30 edges. How many faces are there?
Here:
Number of vertices (V) = 20
Number of edges (E) = 30
Let the number of faces are F. Then using Euler's formula, we have
F + V = E + 2 ...(1)
∴ Substituting the values of V and E in (1), we get
F + 20 = 30 + 2![]() F + 20 = 32
F + 20 = 32![]() F = 32 - 20
F = 32 - 20![]() F = 12
F = 12
Thus, the required number of faces = 12.
An icosahedron is having 20 triangular faces and 12 vertices. Find the number of its edges.
Here:
Number of faces (F) = 20
Number of vertices (V) = 12
Let the number of edges be E.
∴ Using Euler's formula, we have
F + V = E + 2![]() 20 + 12 = E + 2
20 + 12 = E + 2 ![]() 32 = E + 2
32 = E + 2![]() E = 32 - 2 = 30
E = 32 - 2 = 30
Thus, the required number of edges = 30.
What is the least number of planes that can enclose a solid? Name the simplest regular polyhedron and verify Euler’s formula for it.

A tetrahedron has:
4 triangular faces, i.e. F = 4
4 vertices, i.e. V = 4
6 edges, i.e. E = 6
Now, substituting the values of F, V and E in Euler's formula, i.e.
F + V = E + 2
we have
4 + 4 = 6 + 2
Thus, Euler's formula is verified for a tetrahedron.
Name the figure shown here.
(i) How many faces does it have?
(ii) How many vertices does it have?
(iii) How many edges does it have?

Solution not provided.
Ans. Cuboid;
(i) 8
(ii) 8
(iii) 12
Write the number of
(i) faces
(ii) edges
(iii) vertices for a triangular prism.
Solution not provided.
Ans. (i) 5
(ii) 9
(iii) 6
Number of faces of a pyramid is 5. Find the number of its vertices when its edges are 8.
Solution not provided.
Ans. 5
What is Euler’s formula? Using Euler’s formula, find the number of faces of tetrahedron having vertices as 4 and 6 edges.
Solution not provided.
Ans. F + V = E + 2; Four
What is a triangular pyramid? What is a pyramid called if its base is a square?
Solution not provided.
Ans. Square pyramid.
A dice is a cube in which the number on the opposite faces must total 7. Draw its net.
Solution not provided.
Draw the net of a triangular prism whose base is an equilateral triangle.
Solution not provided.
Match the following figures:

Solution not provided.
Ans. (a) - (iii); (b) - (iii); (c) - (i); (d) - (iv)
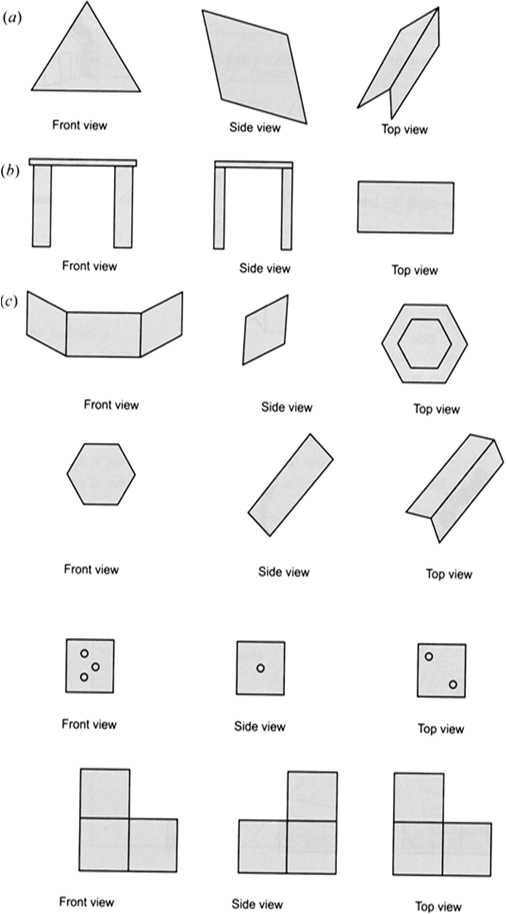
Look at the following figure in which four cubes are combined.

Draw: (i) Its front view.
(ii) Its side view.
(iii) Its top view.
Solution not provided.
Look at the adjoining solid and draw its:
(i) top view.
(ii) front view.
(iii) Side view.
Solution not provided.
What kind of polygon is the base of a tetrahedron?
-
A square
-
A triangle
-
A quadrilateral
B.
A triangle
What do we call a quadrilateral prism, whose ends are parallelograms?
-
A cuboid
-
A parallelopiped
-
An oblique prism
B.
A parallelopipedMock Test Series
Sponsor Area
Sponsor Area