Congruence of Triangles
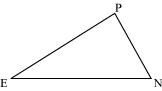
You want to show that ΔART ≅ ΔPEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR = (ii) RT = (iii) AT =
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ? (ii) ?
(a)
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b)
(i) RT = EN
(ii) PN = AT
(c)
(i) ∠ATR = ∠PNE
(ii) ∠RAT = ∠EPN
Sponsor Area
Some More Questions From Congruence of Triangles Chapter
Give any two real-life examples for congruent shapes.
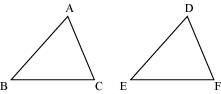
Which congruence criterion do you use in the following?
(a) Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
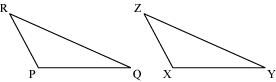
(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
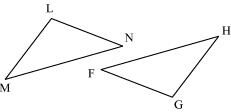
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB
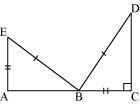
You want to show that ΔART ≅ ΔPEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR = (ii) RT = (iii) AT =
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ? (ii) ?

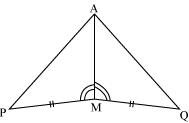
You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
|
– |
Steps |
– |
Reasons |
|
(i) |
PM = QM |
(i) |
… |
|
(ii) |
∠PMA = ∠QMA |
(ii) |
… |
|
(iii) |
AM = AM |
(iii) |
… |
|
(iv) |
ΔAMP ≅ ΔAMQ |
(iv) |
… |
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
In a squared sheet, draw two triangles of equal areas such that
(i) The triangles are congruent.
(ii) The triangles are not congruent.
What can you say about their perimeters?
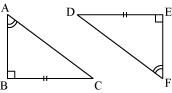
Explain, why
ΔABC ≅ ΔFED
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area