Sponsor Area
Congruence Of Triangles
In a squared sheet, draw two triangles of equal areas such that
(i) The triangles are congruent.
(ii) The triangles are not congruent.
What can you say about their perimeters?
(i)

Here, ΔABC and ΔPQR have the same area and are congruent to each other also. Also, the perimeter of both the triangles will be the same.
(ii)

Here, the two triangles have the same height and base. Thus, their areas are equal. However, these triangles are not congruent to each other. Also, the perimeter of both the triangles will not be the same.
Some More Questions From Congruence of Triangles Chapter
Which congruence criterion do you use in the following?
(a) Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
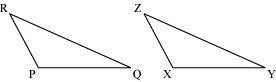
(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
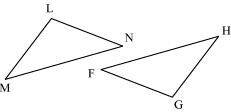
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
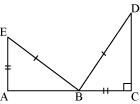
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB




You want to show that ΔART ≅ ΔPEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR = (ii) RT = (iii) AT =
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ? (ii) ?


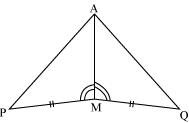
You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
–
Steps
–
Reasons
(i)
PM = QM
(i)
…
(ii)
∠PMA = ∠QMA
(ii)
…
(iii)
AM = AM
(iii)
…
(iv)
ΔAMP ≅ ΔAMQ
(iv)
…
–
Steps
–
Reasons
(i)
PM = QM
(i)
…
(ii)
∠PMA = ∠QMA
(ii)
…
(iii)
AM = AM
(iii)
…
(iv)
ΔAMP ≅ ΔAMQ
(iv)
…

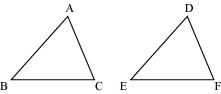
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
In a squared sheet, draw two triangles of equal areas such that
(i) The triangles are congruent.
(ii) The triangles are not congruent.
What can you say about their perimeters?
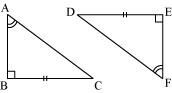
Explain, why
ΔABC ≅ ΔFED

Sponsor Area
Mock Test Series
Mock Test Series





