☰
✕

Areas of Parallelograms and Triangles
Question
Wired Faculty App

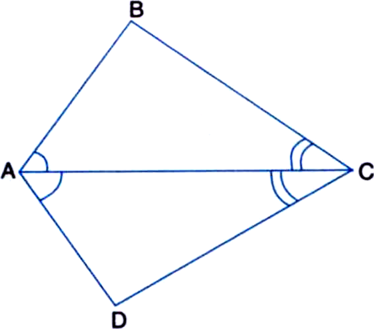
∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∆BCD is a right angle. 

Answer

Given: ∆ABC is an isosceles triangle in which AB = AC.
Side BA is produced to D such that AD = AB.
To Prove: ∠BCD is a right angle.
Proof: ∵ ABC is an isosceles triangle
∴ ∠ABC = ∠ACB    ...(1)
∵ AB = AC and AD = AB
∴ AC = AD

∴ In ∆ACD,
∠CDA = ∠ACD
| Angles opposite to equal sides of a triangle are equal
⇒ ∠CDB = ∠ACD    ...(2)
Adding the corresponding sides of (1) and (2), we get
∠ABC + ∠CDB = ∠ACB + ∠ACD
⇒ ∠ABC + ∠CDB = ∠BCD    ...(3)
In ∆BCD,
∠BCD + ∠DBC + ∠CDB = 180°
| ∵ Sum of all the angles of a triangle is 180°
⇒ ∠BCD + ∠ABC + ∠CDB = 180°
⇒    ∠BCD + ∠BCD = 180°
| Using (3)
⇒    2∠BCD = 180°
⇒    ∠BCD = 90°
⇒ ∠BCD is a right angle.

 

Sponsor Area

Some More Questions From Areas of Parallelograms and Triangles Chapter

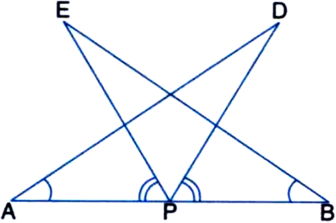
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

 

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

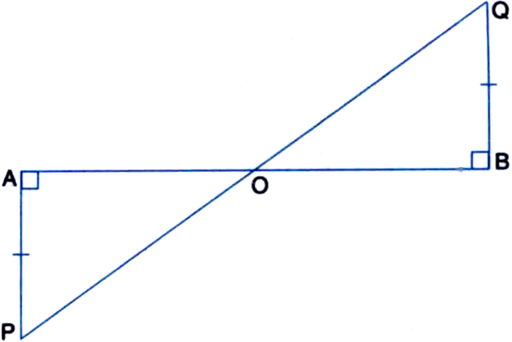
In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

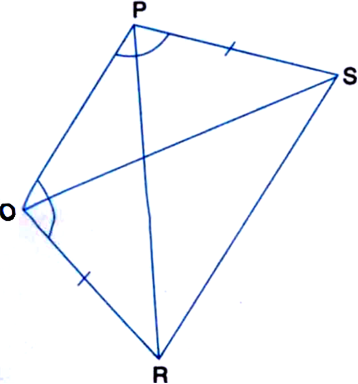
In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i)    ∆APX ≅ ∆BPY
(ii)    AB and XY bisect each other at P.

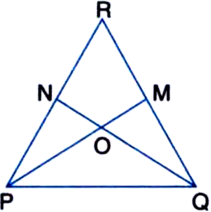
In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

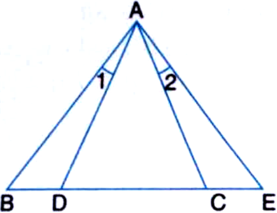
In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.