☰
✕

Areas of Parallelograms and Triangles
Question
Wired Faculty App

ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (see figure). Show that these altitudes are equal.

Answer

Given: ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively.
To Prove: BE = CF.
Proof: ∵ ABC is an isosceles triangle
∴ AB = AC
∴ ∠ABC = ∠ACB    ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆BEC and ∆CFB,
∠BEC = ∠CFB    | Each = 90°
BC = CB    | Common
∠ECB = ∠FBC    | From (1)
∴ ∆BEC ≅ ∆CFB    | By AAS Rule
∴ BE = CF.    | C.P.C.T.

Sponsor Area

Some More Questions From Areas of Parallelograms and Triangles Chapter

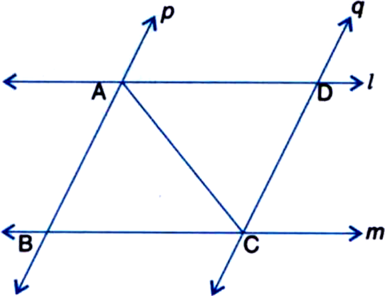
I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.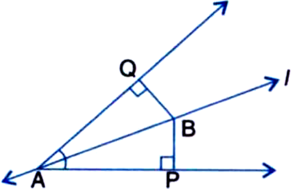

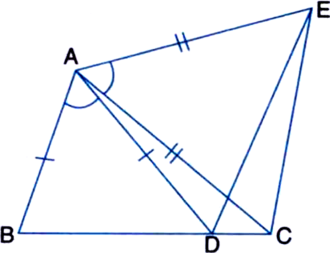
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

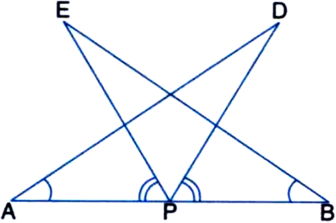
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

 

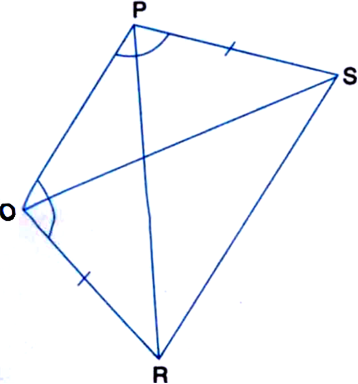
In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

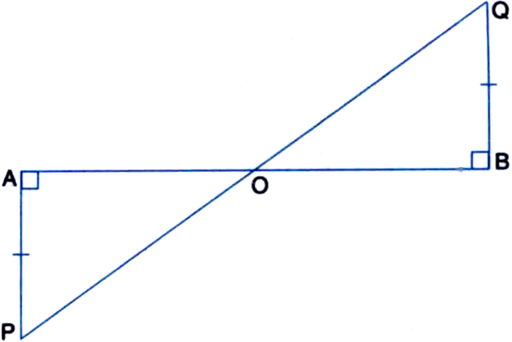
In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

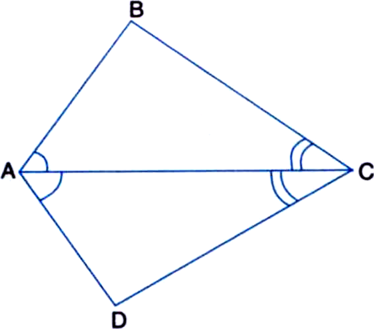
In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i)    ∆APX ≅ ∆BPY
(ii)    AB and XY bisect each other at P.

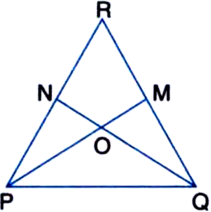
In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.