☰
✕

Areas of Parallelograms and Triangles
Question
Wired Faculty App

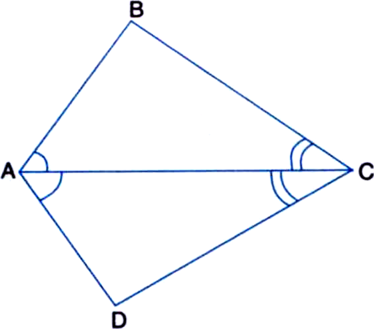
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?

Answer

Given: In quadrilateral ACBD, AC = AD and AB bisects ∠A.
To Prove: ∆ABC ≅ ∆ABD.
Proof: In ∆ABC and ∆ABD,
AC = AD    | Given
AB = AB    | Common
∠CAB = ∠DAB
| ∵ AB bisects ∠A
∴ ∠ABC ≅ ∠ABD    | SAS Rule
∴ BC = BD    | C.P.C.T,

Sponsor Area

Some More Questions From Areas of Parallelograms and Triangles Chapter

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.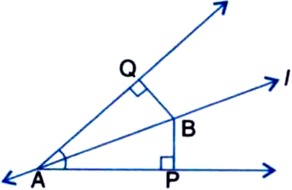

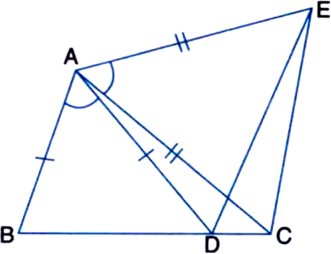
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

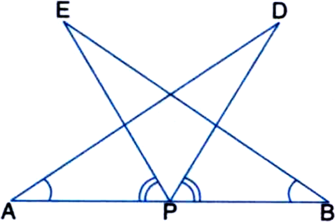
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

 

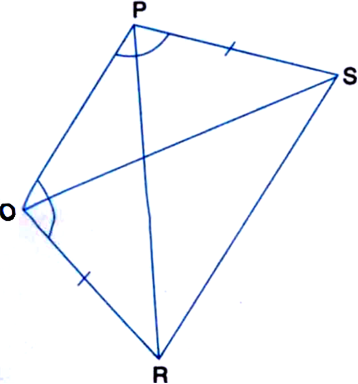
In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

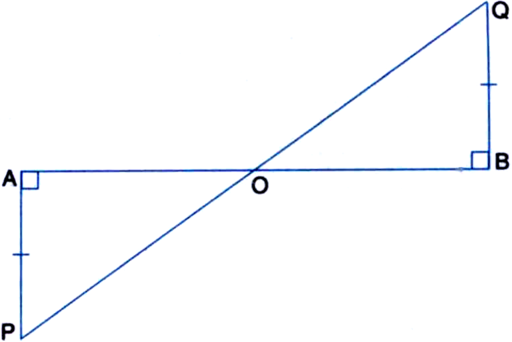
In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i)    ∆APX ≅ ∆BPY
(ii)    AB and XY bisect each other at P.

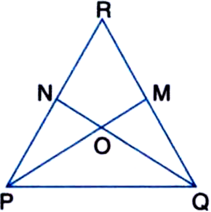
In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.