☰
Circles
In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012
Given: In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively.
To Prove: (i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF.
Proof: (i) In quadrilateral ABED,
AB = DE and AB || DE
| Given
∴ quadrilateral ABED is a parallelogram.
| ∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel
and are of equal length
(ii) In quadrilateral BEFC,
BC = EF and BC || EF | Given
∴ quadrilateral BEFC is a parallelogram.
| ∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel
and are of equal length
(iii) ∵ ABED is a parallelogram
| Proved in (i)
∴ AD || BE and AD = BE ...(1)
| ∵ Opposite sides of a || gm
are parallel and equal
∵ BEFC is a parallelogram | Proved in (ii)
∴ BE || CF and BE = CF ...(2)
| ∵ Opposite sides of a || gm
are parallel and equal
From (1) and (2), we obtain
AD || CF and AD = CF.
(iv) In quadrilateral ACFD,
AD || CF and AD = CF
| From (iii)
∴ quadrilateral ACFD is a parallelogram.
| ∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of equal length
(v) ∵ ACFD is a parallelogram
| Proved in (iv)
∴ AC || DF and AC = DF.
| In a parallelogram opposite sides are parallel and of equal length
(vi) In ∆ABC and ∆DEF,
AB = DE
| ∵ ABED is a parallelogram
BC = EF
| ∵ BEFC is a parallelogram
AC = DF | Proved in (v)
∴ ∆ABC ≅ ∆DEF.
| SSS Congruence Rule
Sponsor Area
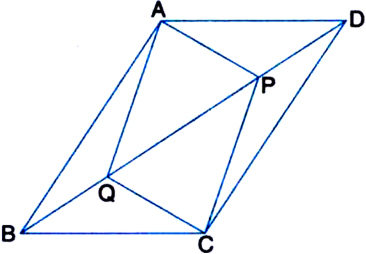
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.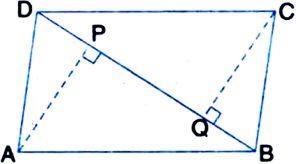
In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram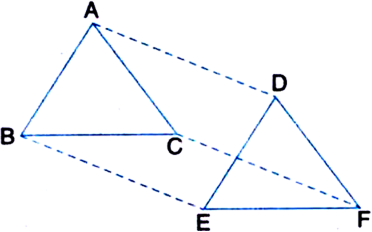
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012
ABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC = ∆BAD
(iv) diagonal AC = diagonal BD.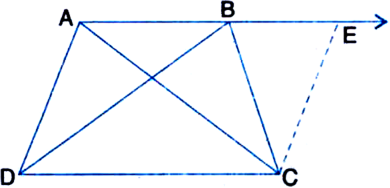
[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Sponsor Area
Sponsor Area