☰
Quadrilaterals
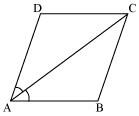
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
Let us extend AB. Then, draw a line through C, which is parallel to AD, intersecting AE at point E. It is clear that AECD is a parallelogram.
(i) AD = CE (Opposite sides of parallelogram AECD)
However, AD = BC (Given)
Therefore, BC = CE
∠CEB = ∠CBE (Angle opposite to equal sides are also equal)
Consider parallel lines AD and CE. AE is the transversal line for them.
∠A + ∠CEB = 180º (Angles on the same side of transversal)
∠A + ∠CBE = 180º (Using the relation∠CEB = ∠CBE) … (1)
However, ∠B + ∠CBE = 180º (Linear pair angles) … (2)
From equations (1) and (2), we obtain
∠A = ∠B
(ii) AB || CD
∠A + ∠D = 180º (Angles on the same side of the transversal)
Also, ∠C + ∠B = 180° (Angles on the same side of the transversal)
∴ ∠A + ∠D = ∠C + ∠B
However, ∠A = ∠B [Using the result obtained in (i)]
∴ ∠C = ∠D
(iii) In ΔABC and ΔBAD,
AB = BA (Common side)
BC = AD (Given)
∠B = ∠A (Proved before)
∴ ΔABC ≅ ΔBAD (SAS congruence rule)
(iv) We had observed that,
ΔABC ≅ ΔBAD
∴ AC = BD (By CPCT)
Sponsor Area
The angles of quadrilateral are in the ratio 3: 5: 9: 13.
Find all the angles of the quadrilateral.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
(i) It bisects ∠C also,
(ii) ABCD is a rhombus.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure).
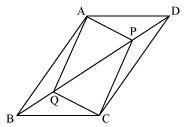
Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
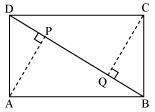
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
Sponsor Area
Sponsor Area