Quadrilaterals
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Let us consider a quadrilateral ABCD in which the diagonals AC and BD intersect each other at O. It is given that the diagonals of ABCD are equal and bisect each other at right angles. Therefore, AC = BD, OA = OC, OB = OD, and ∠AOB = ∠BOC = ∠COD = ∠AOD = 90º. To prove ABCD is a square, we have to prove that ABCD is a parallelogram, AB = BC = CD = AD, and one of its interior angles is 90º.
In ΔAOB and ΔCOD,
AO = CO (Diagonals bisect each other)
OB = OD (Diagonals bisect each other)
∠AOB = ∠COD (Vertically opposite angles)
∴ ΔAOB ≅ ΔCOD (SAS congruence rule)
∴ AB = CD (By CPCT) … (1)
And, ∠OAB = ∠OCD (By CPCT)
However, these are alternate interior angles for line AB and CD and alternate interior angles are equal to each other only when the two lines are parallel.
∴ AB || CD … (2)
From equations (1) and (2), we obtain
ABCD is a parallelogram.
In ΔAOD and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOD = ∠COD (Given that each is 90º)
OD = OD (Common)
∴ ΔAOD ≅ ΔCOD (SAS congruence rule)
∴ AD = DC … (3)
However, AD = BC and AB = CD (Opposite sides of parallelogram ABCD)
∴ AB = BC = CD = DA
Therefore, all the sides of quadrilateral ABCD are equal to each other.
In ΔADC and ΔBCD,
AD = BC (Already proved)
AC = BD (Given)
DC = CD (Common)
∴ ΔADC ≅ ΔBCD (SSS Congruence rule)
∴ ∠ADC = ∠BCD (By CPCT)
However, ∠ADC + ∠BCD = 180° (Co-interior angles)
⇒ ∠ADC + ∠ADC = 180°
⇒ 2∠ADC = 180°
⇒ ∠ADC = 90°
One of the interior angles of quadrilateral ABCD is a right angle.
Thus, we have obtained that ABCD is a parallelogram, AB = BC = CD = AD and one of its interior angles is 90º. Therefore, ABCD is a square.
Sponsor Area
Some More Questions From Quadrilaterals Chapter
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
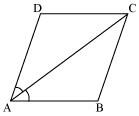
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
(i) It bisects ∠C also,
(ii) ABCD is a rhombus.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
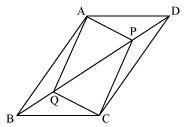
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure).
Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
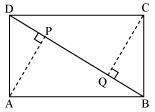
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that
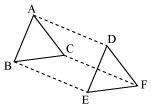
(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) Quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
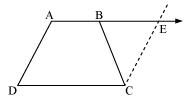
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area