ABCD एक समांतर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमश: लम्ब हैं। दर्शाइए कि:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.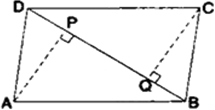
सिद्ध करना है: (i) ∆APB ≅ ∆CQD
(ii) AP = CQ.
प्रमाण: (i) ∆APB और ∆CQD में,
 (ज्ञात है)
(ज्ञात है) (एकान्तर कोण)
(एकान्तर कोण)AB = CD (||gm की सम्मुख भुजाएँ)
∴ ∆APB ≅ ∆CQD (AAS नियम)
(ii) अत: AP = CQ (C.P.C.T.)