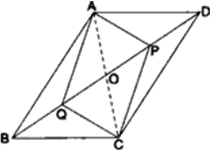
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है दर्शाइए कि   

(i)    ∆APD ≅ ∆CQB
(ii)   AP = CQ
(iii)  ∆AQB ≅ ∆CPD
(iv)  AQ = CP
(v)   APCQ एक समांतर चतुर्भुज है।

ज्ञात है: ABCD एक समांतर चतुर्भुज है। विकर्ण BD पर दो बिंदु P तथा Q इस प्रकार स्थित हैं कि DP = BQ
सिद्ध करना हैं: (i) APCQ एक समांतर चतुर्भुज है। 
(ii) AP = CQ
(iii) AQ = CP
(iv) ∆AQB = ∆CPD
(v) ∆APD ≅ ∆CQB.
रचना: समांतर चतुर्भुज ABCD के विकर्ण AC और BD खींचों जो O पर प्रतिच्छेद करते हैं।
प्रमाण: (i) हम जानते हैं कि एक समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित होते हैं।
∴         OD = OB
परन्तु      DP = BQ        (ज्ञात हैं) 
∴   DO - DP = BO - BQ
या          OP = OQ
और         OA = OC
∴     PQ और AC एक दूसरे को समद्विभाजित करते हैं।
∴  APCQ एक समांतर चतुर्भुज है।
(ii) AP = CQ 
(एक समांतर चतुर्भुज की सम्मुख भुजाएँ) 
(iii) AQ = CQ
  (समांतर चतुर्भुज की सम्मुख भुजाएँ)
(iv) ∆AQB और ∆CPD में,
         AB = CD
              (||gm ABCD की सम्मुख भुजाएँ) 
         AQ = CD
              (||gm AQCP की सम्मुख भुजाएँ)
          QB = DP   (ज्ञात है)             
अत:   ∆AQB ≅ ∆CPD        (SSS नियम)
(v) ∆APD और ∆CQB में,
          AD = BC
                (||gm ABCD की सम्मुख भुजाएँ)
          BQ = PD       (ज्ञात  है) 
          CQ = AP
                 (||gm APCQ की सम्मुख भुजाएँ)
अत: ∆APD ≅ ∆CQB     (SSS नियम)