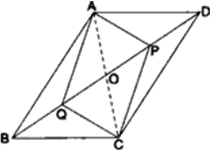
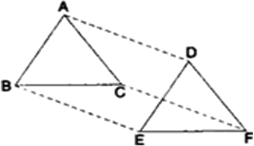
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि (i) ABCD एक वर्ग है (ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।

Solution

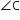ज्ञात है: ABCD एक आयत है जिसमें AC, $angle straight A$ को तथा $angle straight C$ को समद्विभाजित करता है।
सिद्ध करना है:
(i) ABCD एक वर्ग है।
(ii) विकर्ण BD, $angle straight B$ तथा $angle straight D$ को समद्विभाजित करता है।
प्रमाण (i): $increment ACD$ में
   $angle straight A space equals space angle straight C$
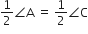
या    $1 half angle straight A space equals space 1 half angle straight C$
अत:    $angle DAC space equals space angle DCA$
AD = CD
[समान कोणों की सम्मुख भुजाएँ]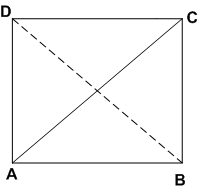
WiredFaculty
अत: ABCD एक समचतुर्भुज है और यह दिया गया है कि यह एक आयत है।
अत: ABCD एक वर्ग है।
(ii) $increment ABD space और space space increment CDB$ में,
AD = CD (वर्ग की भुजाएँ)
AB = BC
और BD = BC (उभयनिष्ठ)
∴    $increment ABD space approximately equal to space increment CBD$
(SSS सर्वगसमता नियम)
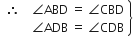$open table attributes columnalign right end attributes row cell therefore space space space space angle ABD space equals space angle CBD end cell row cell angle ADB space equals space angle CDB end cell end table close curly brackets$ (CPCT)
अत: विकर्ण BD, $angle straight B$ तथा $angle straight D$ को समद्विभाजित करता है।