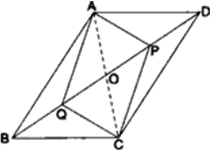
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण समद्विभाजित करते हैं।

Solution

ज्ञात हैं: ABCD एक वर्ग है जिसके विकर्ण O पर प्रतिच्छेद करते हैं।
WiredFaculty
सिद्ध करना है: (i) BD = AC
(ii) OA = OC, OB = OD, (iii) $AC perpendicular BD.$
प्रमाण: (i) $increment DAB space और space space increment CBA space म ें comma$
AB = BA (उभयनिष्ठ)
AD = BC (वर्ग भुजाएँ)
   $angle DAB space equals space angle CBA space equals space 90 degree$ (वर्ग के कोण)
अत:    $increment DAB space approximately equal to space increment CBA$ (SAS नियम)
इसलिए BD = AC (CPCT)
(ii) $increment AOB space और space space increment COD space म ें$
   $angle AOB space equals space angle COD$ (शीर्षाभिमुख कोण)
AB = CD (वर्ग की भुजाएँ)
   $angle OBA space equals space angle OCD$ (एकान्तर कोण)
∴ $increment AOB space approximately equal to space increment COD$ (AAS नियम से)
अत: OA = OC और OB = OD
(iii) $increment AOD space और space space increment COD$ में,
OA = OC (ऊपर सिद्ध किया है)
AD = CD (वर्ग की भुजाएँ)
OD = OD (उभयनिष्ठ)
इसलिए $increment AOD space approximately equal to space increment COD$ [SSS नियम से)
इस प्रकार $angle AOD space equals space angle COD$ (CPCT)
और    $angle AOD space plus space angle COD space equals space 180 degree$ (रैखिक युग्म)
   $WiredFaculty$
अत: $AC thin space perpendicular space BD.$