दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर समद्विभाजित करें, तो वह एक वर्ग होता है।

Solution

ज्ञात है: एक चतुर्भुज ABCD जिसमें AC = BD और AC तथा BD एक दूसरे को समकोण पर प्रतिच्छेद करते हैं।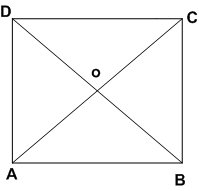
WiredFaculty
सिद्ध करना है: ABCD एक वर्ग है।
प्रमाण: $increment AOB space और space space increment COD$ में
OA = OC (ज्ञात है)
OB = OD (ज्ञात है)
$angle AOB space equals space angle COD$ (शीर्षाभिमुख कोण)
   $increment AOB space approximately equal to space increment COD$ (SAS नियम)
  इसलिए AB = CD (C.P.C.T.)
और $angle OAB space equals space angle OCD$
जो कि एकान्तर कोणों का युग्म है
$therefore space space AB space parallel to space CD$
अब AB = CD और $AB parallel to CD$
अत: ABCD एक समान्तर चतुर्भुज है।
$increment AOD thin space और space space increment COD$ में,
OD = OD (उभयनिष्ठ)
$angle AOD space space equals space angle COD space equals space 90 degree$   (ज्ञात है)
OA = OC (ज्ञात है)
$therefore space space space increment AOD space approximately equal to space space increment COD$ (SAS नियम)
$therefore space space space space space space space space space space space space AD space equals space CD$ (C.P.C.T.)
इसी प्रकार, AB = BC = CD = DA और ABCD एक समचतुर्भुज है।
परन्तु इसके विकर्ण समान हैं,
$therefore$ ABCD एक वर्ग है।