Deduce a relation between focal length (f) and radius of curvature (R) for a concave mirror.

Relation between focal length and Radius of curvature for a concave mirror:

Consider a concave mirror and a ray AB which is parallel to the principal axis and incident at the point B. After reflection from the mirror, this ray passes through its focus F as per the laws of reflection. If C is the cente of curvature, then CP = R, is the radius of curvature and CB is normal to the mirror at point B.

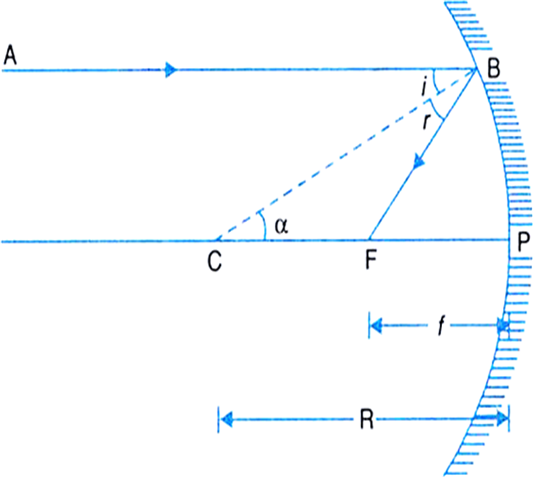
Fig. Relation between f and R for a concave mirror.

Now, according to the law of reflection, 
Angle of incidence = Angle of reflection
i.e.,                    ∠ i = ∠ r            ...(1) 

In $∆\mathrm{BCF},$
As AB is parallel to CP, so 

                       ∠α = ∠i             (Alternate angles)

∴                    ∠ α = ∠ r 
Thus, ∆ BCF is isosceles.
Hence, CF = FB. 

If the aperture (or size) of the mirror is small, then B lies close to P, so that, 

                                $\mathrm{FB} \simeq \mathrm{FP}$ 

$\therefore$                            $\mathrm{FP} = \mathrm{CF} = \frac{1}{2}\mathrm{CP}$ 

i.e.,                           $\boxed{\mathrm{f} = \frac{\mathrm{R}}{2}}$ 

$\Rightarrow$ $\mathrm{Focal} \mathrm{length} = \frac{1}{2}\times \mathrm{Radius} \mathrm{of} \mathrm{curvature}.$ 

Thus, the principal focus of a spherical mirror lies midway between the pole and the centre of curvature.

Hence proved.