Define acceleration due to gravity. Deduce an expression for it in terms of mass of the earth (M) and universal gravitational constant (G).

Acceleration due to gravity:
Acceleration produced in the motion of a body falling under the force of gravity is called acceleration due to gravity.
It is denoted by ‘g’.

Relation between g and G
Consider the earth as a sphere of mass M and radius R, as shown in Fig.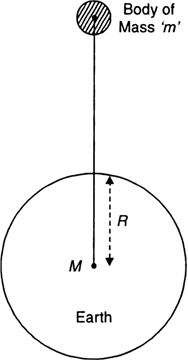
  
Fig. To determine ‘g’.
Consider a body of mass 'm' situated at distance 'r' from the centre of the earth.
According to Newton's law of gravitation, the force of attraction between the earth and the body is given by, 
 
                          

This force of gravity produces on acceleration ‘g’, called acceleration due to gravity in the body of mass m.
Hence, from Newton's second law,
F = Mass x Acceleration = mg            ...(2)
From equations (1) and (2), we get 
     
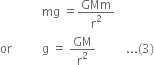
The above derived equation gives acceleration due to gravity at points far away from the earth.
If body is located on the surface of the earth, then r = R, the radius of the earth.
The above equation becomes, 

This equation gives acceleration due to gravity at the surface of the earth. 

The value of 'g' is almost constant near the surface of the earth because the radus of the earth does not change much over it's entire surface. 

The value of ‘g’ on earth’s surface = 9.8 ms^-2.