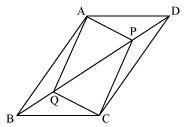
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
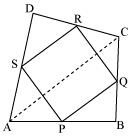
(i) SR || AC and SR = AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
(i) In ΔADC, S and R are the mid-points of sides AD and CD respectively.
In a triangle, the line segment joining the mid-points of any two sides of the triangle is parallel to the third side and is half of it.
∴ SR || AC and SR = AC … (1)
(ii) In ΔABC, P and Q are mid-points of sides AB and BC respectively. Therefore, by using mid-point theorem,
PQ || AC and PQ = AC … (2)
Using equations (1) and (2), we obtain
PQ || SR and PQ = SR … (3)
⇒ PQ = SR
(iii) From equation (3), we obtained
PQ || SR and PQ = SR
Clearly, one pair of opposite sides of quadrilateral PQRS is parallel and equal.
Hence, PQRS is a parallelogram.