State Huygen’s principle in the wave theory of light. Using the principle, prove the laws of reflection of light. 

(i) Every point on the given wave front, called primary wave front, acts as a fresh source of new disturbance, called secondary waveless, which travel in all directions with the velocity of light in the medium.

(ii) A surface touching these secondary wavelets, tangentially in the forward direction at any instant gives the new wave front at that instant. This is called secondary wave front.

Reflection on the basis of wave theory :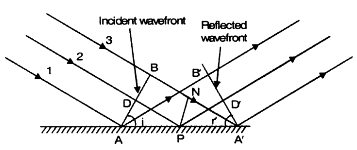
 

According to Huygen’s principle, every print on AB is a source of secondary wavelets. Let the secondary wavelets from B strike. M₁ M₂ at A' in t seconds.

BA' = Ct                         ...(i)

where C is the velocity of light in the medium.

The secondary wavelets from A will travel the same distance C x t in the same time. Therefore, with A as a centre and C x t as radius, draw an arc B', so that,

AB' = Ct                         ...(ii)

For A'B' to be the reflected wave front, secondary wavelets starting from any other point D on the incident wave front AB must reach the corresponding point D' on A' B' after reflection at P, in exactly the same time as the secondary wavelets take to go from B to A.

For this, DP + PD' = BA'    ...(iii)

To prove it, draw PN ⊥ BA'

DP = BN                        ...(iv)

In As. AA'B and AA'B'

AA' is common

∠ABA' = ∠AB'A' = 90° and BA' = AB' = Ct

Therefore As are congruent.

∴    ∠BAA' =