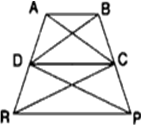
आकृति में, ar(ΔDRC) = ar(ΔDPC) और ar(ΔBDP) = ar(ΔARC) हैं। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलम्ब हैं। 
 

ज्ञात है: चतुर्भुज ABCD और चतुर्भुज DCPR इस प्रकार हैं कि 
  ar(ΔDRC) = ar(ΔDPC)
और ar(ΔBDP) = ar(ΔARC)
सिद्ध करना है: (i) चतुर्भुज DCPR एक समलम्ब है।
(ii) चतुर्भुज ABCD एक समलम्ब है। 
प्रमाण: (i) ar(ΔDRC) = ar(ΔDPC)
ar(ΔDRC) और (ΔDPC) एक ही आधार DC पर स्थित हैं और उनके क्षेत्रफल भी समान हैं।
∴       DC || RP
अत:     DCPR एक समलम्ब है।
अब, 
 ar(ΔBDP) = ar(ΔARC)
या  ar(ΔBCD) + ar (ΔDPC) = ar(ΔADC) + ar(ΔDRC)
∴   ar(ΔBCD) = ar(ΔADC)
अब, ΔACD और ΔADC एक ही आधार DC पर स्थित हैं और उनके क्षेत्रफल समान हैं।
∴       AB || DC
अत:     ABCD एक समलम्ब है।