☰
✕

त्रिभुज
Question
Wired Faculty App

आकृति में ΔABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD⊥BC, OE⊥AC और OF⊥AB है। दर्शाइए कि
(i) OA2 + OB2 + OC2 - OD2 - OE2 - OF2 = AF2 + BD2 + CE2,
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2

Answer

(i)  समकोण ΔOFA में,
     OA2 = AF2 + OF2     ...(i)
     समकोण ΔOBD में,
     OB2 = OD2 + BD2    ...(ii)
     समकोण ΔOEC में,
     OC2 = OE2 + CE2     ...(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर, हमें प्राप्त होता है:
     OA2 + OB2 + OC2 = AF2 + OF2 + OD2 + BD2 + OE2 + CE2
⇒   OA2 + OB2 + OC2 = AF2 + BD2 + CE2 + OD2 + OF2 + OE2
⇒   AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OF2 - OE2
(ii) AF2 + BD2 + CE2 = (OA2 - OE2) + (OB2 - OF2) + (OC2 - OD2)
     = AE2 + CD2 + BF2
अत:,   AF2 + BD2 + CE2 = AE2 + CD2 + BF2

Sponsor Area

Some More Questions From त्रिभुज Chapter

सभी वृत्त ______ होते हैं। (सर्वांगसम, समरूप)

सभी वर्ग ______ होते हैं। (समरूप, सर्वांगसम)

सभी ______ त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)

भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि (i) उनके संगत कोण ______ हो तथा (ii) उनकी संगत भुजाएँ ______ हों। (बराबर, समानुपाती)

निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ     (ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।

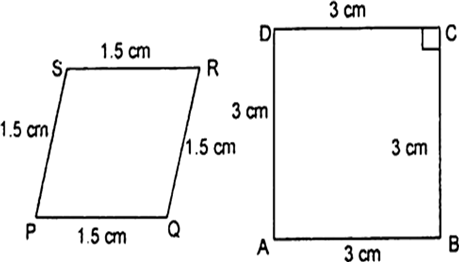
बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं: