System of Particles and Rotational Motion
ABC is the right-angled triangular plane of uniform thickness. The sides are such that AB>BC as shown in the figure. I1, I2, I3 are moments of inertia about AB, BC and AC, respectively. Then which of the following relations is correct?
I1 = I2 = I3
I2 > I1> I3
I3<I2<11
I3>I1>I2
B.
I2 > I1> I3
The moment of inertia of a body about an axis depends not only on the mass of the body but also on the distribution of mass about the axis. For a given body mass is the same, so it will depend only on the distribution of mass about the axis. The mass is farthest from axis BC, so I2 is maximum mass is nearest to axis AC, so I3 is minimum.
Hence, the correct sequence will be I2>I1>I3
Sponsor Area
Some More Questions From System of Particles and Rotational Motion Chapter
Angular momentum of the particle rotating with a central force is constant due to
Four point masses, each of value m, are placed at the corners of a square ABCD of side A. The moment of inertia through A and parallel to BD is
A wire elongates by
A ‘T’ shaped object with dimensions shown in the figure, is lying on a smooth floor. A force F is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect to C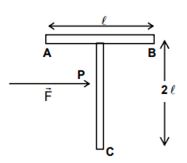
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area