Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken.

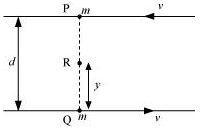
Let at a certain instant two particles be at points P and Q, as shown in the following figure.

L_p = mv × 0 + mv × d 
    =  mvd                                   ...(i) 

Angular momentum of the system about point Q, 
L_Q = mv × d + mv × 0  
    =  mvd                                   ...(ii) 

Consider a point R, which is at a distance y from point Q.
i.e.,               QR = y 

∴                   PR = d – y  
Angular momentum of the system about point R, 
L_R = mv × (d - y) + mv × y 

    = mvd - mvy + mvy 

    = mvd                                   ...(iii) 

Comparing equations (i), (ii), and (iii), we get
L_P = L_Q = L_R                              ...(iv)
From equation (iv), we infer that that the angular momentum of a system does not depend on the point about which it is taken.